题目
给定一个 \(\{1,2,3,\dots,n\}\) 的排列 \(p_1,p_2,p_3,\dots,p_n\)。
求这个排列有多少个非空子序列 \(b_1,b_2,\dots,b_k\),满足这个子序列是一个“好的子序列”。
答案对于 998244353 取模。
如果一个子序列是一个“好的子序列”,那么必须有:
-
\(1\le k\le n\),且对于任意的 \(1\le i<k\),都有 \(b_i<b_{i+1}\);
-
对于任意的 \(1\le i<k\),都有 \(p_{b_i}<p_{b_{i+1}}\);
-
不存在 \(1\le j<b_1\),使得 \(p_j<p_{b_1}\);
-
不存在 \(b_k<j\le n\),使得 \(p_{b_k}<p_{j}\);
-
对于任意的 \(1\le i<k\),都不存在 \(b_i<j<b_{i+1}\),使得 \(p_{b_i}<p_j<p_{b_{i+1}}\);
对于 \(100\%\) 的数据,满足 \(1\le n\le 2\times 10^5\)。
分析
LGIS: "Longest Greedily Increasing Subsequence"
不要问为什么,问就是
我自己造的名字。
可以发现,这些限制中,限制 5 是最复杂的,其余都容易处理。
那么容易想到一个 DP,设 \(f_i\) 表示以 \(i\) 结尾的子序列中,有多少个满足限制 1、2、3 和 5。最后一个限制 4 我们可以单独处理。转移的具体形式比较简单,此处略去。我们重点考察一下对于 \(j<i\),\(j\) 可以称为 \(i\) 的转移点的条件。
首先,若 \(p_j>p_i\),那么 \(j\) 肯定不能称为转移点;其次,如果 \(k<j<i\),且 \(p_k<p_j\),那么 \(k\) 也不可能成为 \(i\) 的转移点。其实这就是题目条件的等价描述。因此,最终我们可以得到的转移点大致长成:
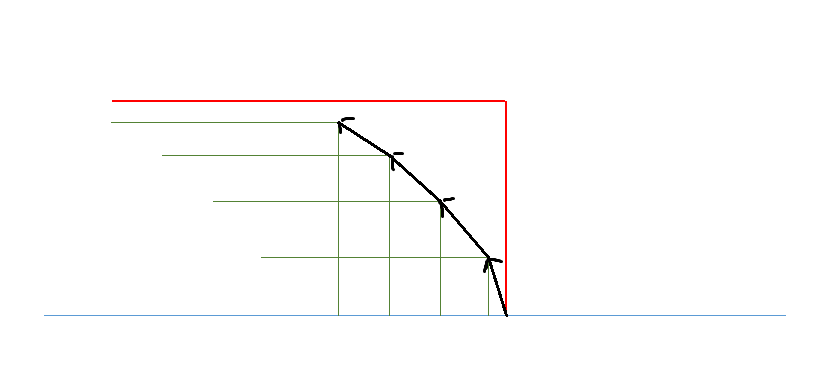
观察一个这个形式:如果我们可以按照值从小到大加入,那么我们只需要求序列上一个前缀的一条贪心反链,也就是一条(反向)极长贪心上升子序列。同时我们还需要支持动态单点修改。
这其实是一个线段树的经典问题。考虑线段树的一个结点和它的左右儿子。如果贪心选取,那么进入这个结点时,我们可以得到一个 \(x\),为已经选中的序列中的最大值。此时,我们会先进入右儿子,再进入左儿子,直到到达叶子再检查是否可以接到 \(x\) 之后——看上去和暴力没有区别......
但我们可以进行优化:
-
如果右儿子的最大值 \(\le x\),那么右儿子中肯定不会有任何一个元素被选中,因此可以直接进入左儿子;
-
如果右儿子最大值 \(>x\),那么右儿子的最大值一定会被选中。此时我们知道了从右儿子出来之后的 \(x'\),并且这个值不会随 \(x\) 变化。因此,我们可以在线段树上预处理出 \(x=x'\) 时,左儿子的结果。
最终我们可以以 \(O(\log^2n)\) 的复杂度维护修改、回答查询。最终的复杂度即为 \(O(n\log^2n)\)。
小结:
-
学习了解一下用线段树维护贪心上升子序列的方法。更重要的启发是,具有贪心结构的过程常常可以用数据结构很好地维护;
-
注意一下第二种情况下的剪枝——找出不变量并利用这个信息预处理。
代码
#include <cstdio>
#include <algorithm>
#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )
const int mod = 998244353;
const int MAXN = 2e5 + 5;
template<typename _T>
void read( _T &x ) {
x = 0; char s = getchar(); bool f = false;
while( s < '0' || '9' < s ) { f = s == '-', s = getchar(); }
while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
if( f ) x = -x;
}
template<typename _T>
void write( _T x ) {
if( x < 0 ) putchar( '-' ), x = -x;
if( 9 < x ) write( x / 10 );
putchar( x % 10 + '0' );
}
template<typename _T>
_T MAX( const _T a, const _T b ) {
return a > b ? a : b;
}
template<typename _T>
_T MIN( const _T a, const _T b ) {
return a < b ? a : b;
}
int stk[MAXN], top;
int lim;
int mx[MAXN << 2];
int visib[MAXN << 2];
int pre[MAXN], suf[MAXN];
int att[MAXN], dp[MAXN], pos[MAXN];
int N;
inline int Mul( int x, int v ) { return 1ll * x * v % mod; }
inline int Sub( int x, int v ) { return ( x -= v ) < 0 ? x + mod : x; }
inline int Add( int x, int v ) { return ( x += v ) >= mod ? x - mod : x; }
int Calc( const int x, const int l, const int r, const int lim ) {
if( l == r ) return lim < mx[x] ? dp[l] : 0;
int mid = ( l + r ) >> 1;
if( lim >= mx[x << 1 | 1] ) return Calc( x << 1, l, mid, lim );
return Add( visib[x], Calc( x << 1 | 1, mid + 1, r, lim ) );
}
inline void Upt( const int x, const int l, const int r ) {
int mid = ( l + r ) >> 1;
mx[x] = MAX( mx[x << 1], mx[x << 1 | 1] );
visib[x] = Calc( x << 1, l, mid, mx[x << 1 | 1] );
}
void Change( const int x, const int l, const int r, const int p, const int nVal ) {
if( l == r ) { mx[x] = nVal; return ; }
int mid = ( l + r ) >> 1;
if( p <= mid ) Change( x << 1, l, mid, p, nVal );
else Change( x << 1 | 1, mid + 1, r, p, nVal );
Upt( x, l, r );
}
int Query( const int x, const int l, const int r, const int segL, const int segR ) {
if( segL > segR ) return 0;
if( segL <= l && r <= segR ) {
if( mx[x] <= lim ) return 0;
int ret = Calc( x, l, r, lim );
lim = mx[x]; return ret;
}
int mid = ( l + r ) >> 1, ret = 0;
if( mid < segR ) ret = Add( ret, Query( x << 1 | 1, mid + 1, r, segL, segR ) );
if( segL <= mid ) ret = Add( ret, Query( x << 1, l, mid, segL, segR ) );
return ret;
}
int main() {
read( N );
rep( i, 1, N ) read( att[i] ), pos[att[i]] = i;
pre[0] = N, suf[N] = 0;
rep( i, 1, N ) pre[i] = MIN( pre[i - 1], att[i] );
per( i, N, 1 ) suf[i] = MAX( suf[i + 1], att[i] );
int ans = 0;
rep( v, 1, N ) {
int i = pos[v];
if( pre[i - 1] >= v ) dp[i] = 1;
else lim = 0, dp[i] = Query( 1, 1, N, 1, i - 1 );
if( suf[i + 1] <= v ) ans = Add( ans, dp[i] );
Change( 1, 1, N, i, v );
}
write( ans ), putchar( '\n' );
return 0;
}