Beautiful Set
Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=5321
Mean:
给出一个集合,有两种计算集合的值的方式:
1 对于集合的一种排列方式,求它任意区间的gcd,将所有区间的gcd值加起来,即为该排列方式的值;将集合所有排列方式的值加起来即为集合的值;
2 对于集合,任意取k个数,对于取出k个数,值为k个数的gcd*k;k从1-n(集合总个数),加起来即为集合的值如果集合的值相同,则输出该值,否则输出较大的值。
analyse:
详细分析:http://blog.csdn.net/firstlucker/article/details/47128347
对于方式1,我们计算gcd为i有多少种情况
令F[i]表示gcd为i的倍数的情况总数
则F[i]=∑C(cnt[i],k)*k!*(n-k+1)!
k从1到cnt[i] cnt[i]为集合中i的倍数的数的个数
根据莫比乌斯函数(其中d为n的倍数)
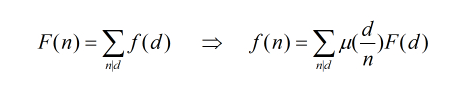
这样就可以先根据公式算出F[i]的值,预处理出莫比乌斯函数的系数,再采用类似素数筛的方式算出f[i],f[i]为gcd为i的情况数,则答案为∑i*f[i] (i从1-集合的最大值).
同理:对于方式2, F[i]=cnt[i]*2^(cnt[i]-1) 同上采用莫比乌斯反演算出f[i],答案即为 ∑i*f[i] (i从1-集合的最大值)
最后比较2个答案,选取较大的值输出即可。
两种形式,用于容斥原理的简化,预处理出系数(nlongn)即可建边算出答案
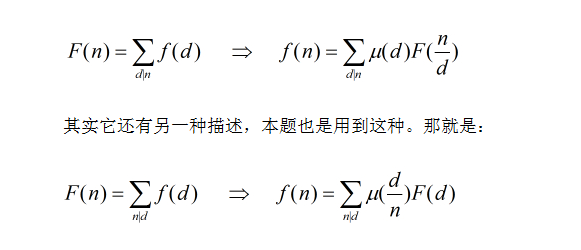
Time complexity: O(N*logN)
Source code: