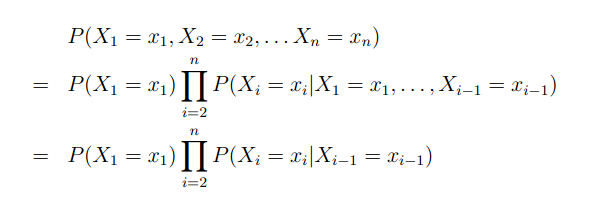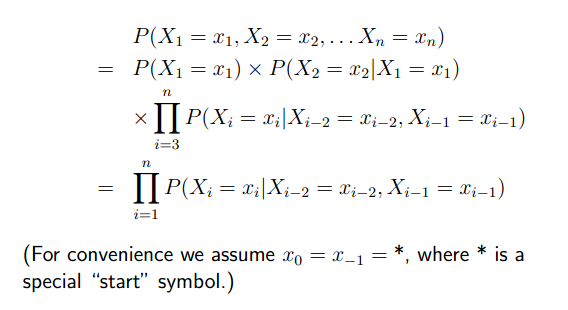在0-1中提到了,当最终output的p=0时,这个时候模型无法正常使用,为了解决这个问题,在0-4中会有所提及。
在本节中,其实,计算概率的时候,我们应该假设某一个位置的词与它前面的所有词都是相关的,但是,如果我们这样计算的话,可以计算出来,计算量是相当大的。例如在p(x1,x2,x3…xn)中,x是集合V中的一个单词,假设v的大小为|v|,也就是说(x1,x2…xn)就一共有|v|的n次方中可能。提出了马尔可夫过程来解决。在计算P的时候,实际上我们给出了一个独立性假设,这个独立性假设就是说所有的随机变量只于它前面的随机变量条件相关。
其实不难理解:
- 假设,有一串随机的变量X1,X2,…XN.(a sequence of random variables)
- 每一个变量可以设置成任何值,并且这些值来自于有限的集合V。(each random variable can take any value in a finite set V)
- 目前,我们把N的值设置成定值。(for now we assume the lenght n is fixed)
我们的目标是计算:
P(X1=x1,X2=x2,X3=x3…Xn=xn)也就是计算0-1中提到的p(x1,x2,x3…xn)
第一种计算P的方法是First-Order Markov Processes,一阶马尔可夫过程
现在来解释一下这个公式:
其实,计算概率的时候,我们应该假设某一个位置的词与它前面的所有词都是相关的,但是,如果我们这样计算的话,可以计算出来,计算量是相当大的。例如在p(x1,x2,x3…xn)中,x是集合V中的一个单词,假设v的大小为|v|,也就是说(x1,x2…xn)就一共有|v|的n次方中可能。
所以,为了简化问题,在一阶马尔可夫过程中,我们只假设当前的词至于前面的一个单词相关,所以得到了上图中的公式。
也就是说,在一阶马尔可夫过程中:
for any i属于{2….n},for any x1,x2…xi
P(Xi=xi|X1=x1…Xi-1=xi)=P(Xi=xi|Xi-1=xi-1)
那么,同理,我们也可以假设当前的单词,至于前面的两个单词相关,这样,就出现了二阶马尔可夫过程。
Second-Order Markov Processes
为了表示方便,引入了*来代表x0,x-1
如果上面的公式推导看着比较费劲,那么需要补充一下概率知识,建议阅读相关资料。这里稍微普及一下:
例如:
p(a,b)=p(a)*p(b|a)
p(a,b,c)=p(a)*p(b|a)*p(c|a,b)
在一些英文文献中p(b|a)有的时候被写作conditional probability of p of b given a.
在这一节中,我们把n的值设置成了定值,在下一节中,将会讨论,n的值可变的时候怎么办。