1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
(1)导图:
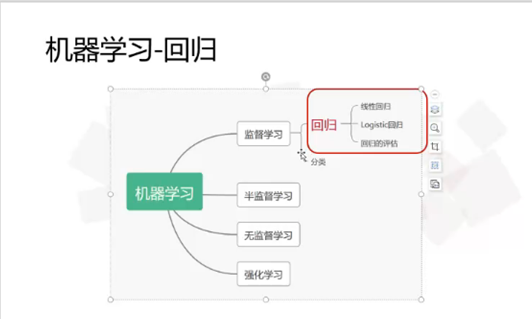
(2)回归与分类的区别:

(3)个各维数组及数组的类型,矩阵特性
Ⅰ、

Ⅱ、

(4)线性回归算法公式:
y=w*x+b
其中b为偏置,y为要预测的结果
(5)误差问题
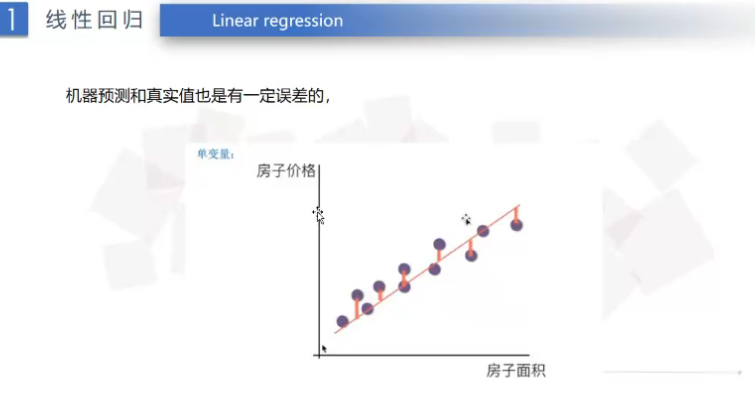
利用迭代算法减小误差:(理解)

(6)线性回归算法缺点优化及策略:
此方法仅供了解:

梯度下降法:

不断迭代学习后的结果:
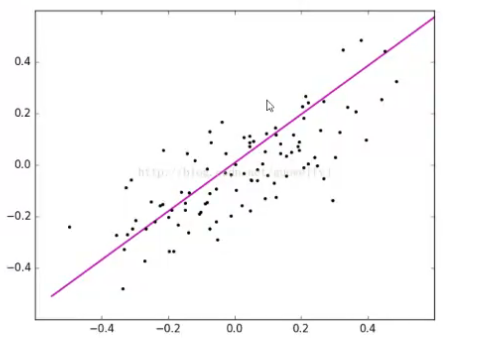
此方法代码:
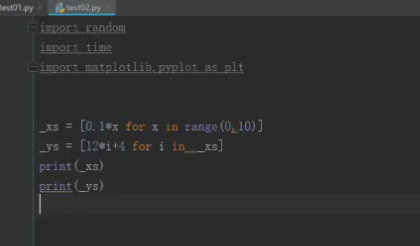

迭代100次结果:

越来越接近真实值。
增加a,b后代码:
结果:
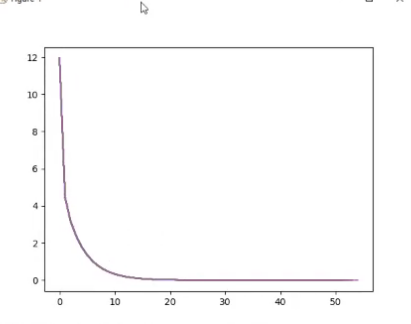
2.思考线性回归算法可以用来做什么?
(1)可以用线性回归算法制作的模型来预测股市走向。
(2)可以用来预测电视机的价格。
(3)可以用来分析预测汽车百公里耗油走向。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。
答:
线性回归预测房价
数据为网上爬取的房价信息:
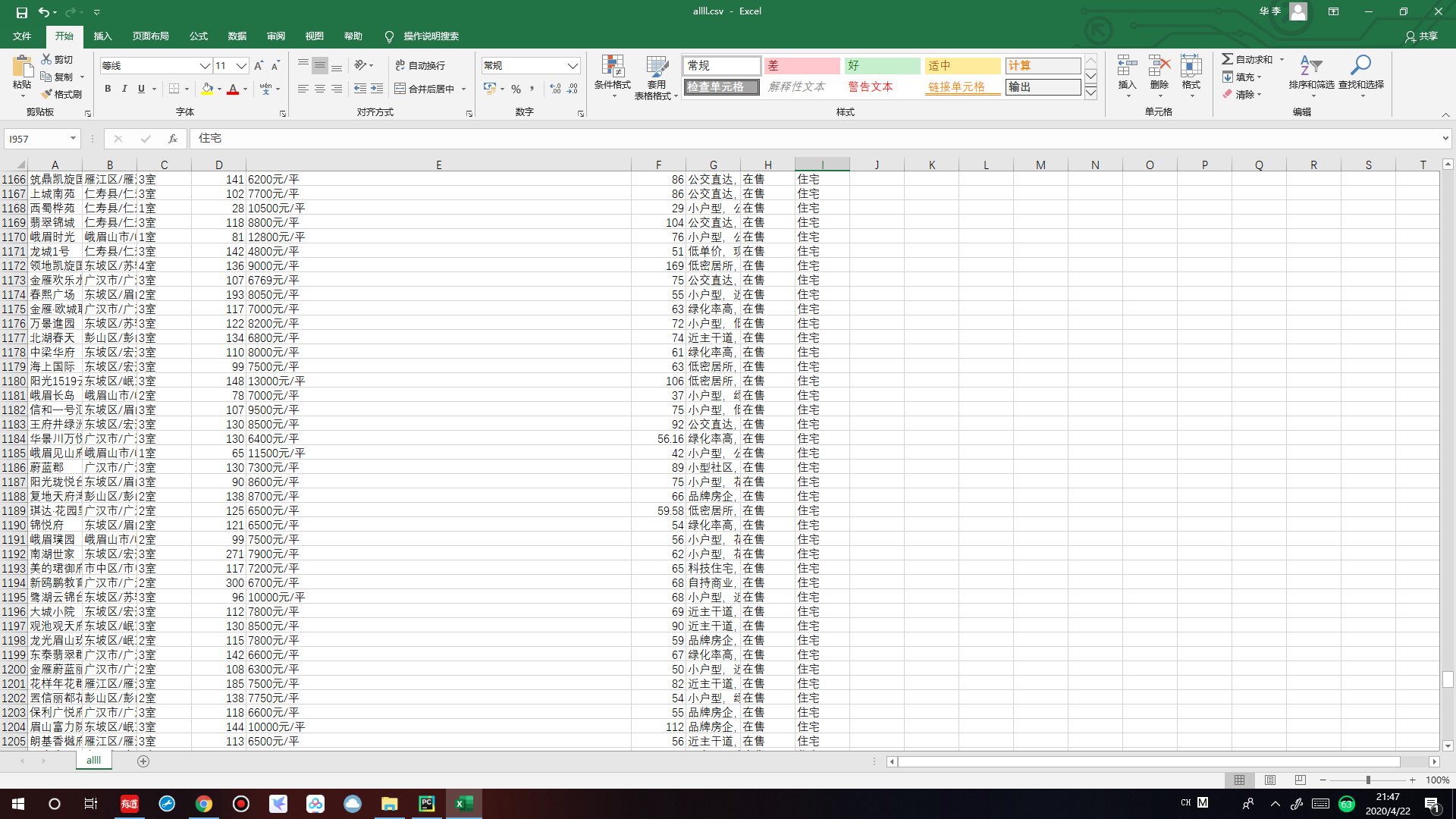
代码为:
import pandas as pd import numpy as np from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split data = pd.read_csv(r'D:lianjiashujvallll.csv', encoding='utf-8') #引入数据 X = data['房间面积'] #引入需要处理的数据属性 y = data['起价'] clf = LinearRegression() # 构建线性回归模型 print('建立的LinearRegression模型为:', ' ', clf) #图 import matplotlib.pyplot as plt from matplotlib import rcParams rcParams['font.sans-serif'] = 'SimHei' #绘图可显示中文 fig = plt.figure(figsize=(10,6)) f1 = np.polyfit(X, y, 3) print('f1 is : ', f1) p1 = np.poly1d(f1) print('p1 is : ', p1) yvals=np.polyval(f1, X) plt.scatter(X, y, color="blue", label='original values') plt.plot(X, yvals, label='polyfit values') plt.title('Regression analysis') plt.show()
结果输出为:

