数组循环移位

【例1】循环左移1位

输入10个整数到数组a中，将数组各元素依次循环左移一个位置（如下图1），输出移动后的数组a。

图1  数组元素循环左移1位

• 编程思路

先将a[0]保存起来（t=a[0]），再用一个循环将a[1]~a[9]依次前移一位，最后将预存起来的a[0]送至a[9]即可。

• 源程序及运行结果

#include <iostream>

using namespace std;

int  main( )

{

   int  a[10],i,t ;                          

   for (i=0;i<10;i++)

       cin>>a[i];

   t=a[0];

   for(i=0;i<9;i++)

       a[i]=a[i+1];

   a[9]=t;

   for (i=0;i<10;i++)

   cout<<a[i]<<"   ";

   cout<<endl;

   return 0;

}

编译并执行以上程序，得到如下所示的结果。

1 2 3 4 5 6 7 8 9 10

2   3   4   5   6   7   8   9   10   1

Press any key to continue

【例2】循环左移P位

设有n（n>1）个整数存放在一维数组R中。试设计一个在时间和空间两方面尽可能高效的算法。将R中的序列循环左移P（0<P<n）个位置，即将R中的数据由（X₀，X₁，…X_n-1）变换为（X_p，X_p+1，…，X_n-1，X₀，X₁，…，X_p-1）。

• 编程思路1

上一个实例中，程序段：

   t=a[0];

   for(i=0;i<9;i++)

       a[i]=a[i+1];

   a[9]=t;

实现了循环左移1位。将这个程序段循环执行p次，即可完成循环左移p位的操作。

按这一思路所设计的算法的时间复杂度为O（p*n），空间复杂度为O（1）。

• 源程序1及运行结果

#include <iostream>

using namespace std;

int main()

{

    int  r[10]={1,2,3,4,5,6,7,8,9,10};

    int i,p,t,times;

    cout<<"请输入需要左移的次数p （0<p<10):";

       cin>>p;

    cout<<"数组初始情况为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

    for(times=1;  times<=p; times++)

       {

      t=r[0];

      for(i=0;i<9;i++)

          r[i]=r[i+1];

      r[9]=t;

    }

    cout<<"循环左移"<<p<<"位后，数组变换为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

    return 0;

}

编译并执行以上程序，得到如下所示的结果。

请输入需要左移的次数p （0<p<10):4

数组初始情况为：1  2  3  4  5  6  7  8  9  10

循环左移4位后，数组变换为：5  6  7  8  9  10  1  2  3  4

Press any key to continue

• 编程思路2

定义一个可以放下p个整数的辅助数组temp，将数组R中的前p个整数依次存入辅助数组temp中，将R中后面的n-p个整数依次前移p个位置，将辅助数组中的数据依次取出，放入R中第n-p个整数开始的位置。

按这一思路所设计的算法的时间复杂度为O（n），空间复杂度为O（p）。

• 源程序2

#include <iostream>

using namespace std;

int main()

{

    int  r[10]={1,2,3,4,5,6,7,8,9,10};

    int temp[10];         // 辅助数组，存放要移出的整数

    int i,p;

    cout<<"请输入需要左移的次数p （0<p<10):";

       cin>>p;

    cout<<"数组初始情况为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

       for(i=0;i<p;i++)       // 将R中前p个数据存入辅助数组中

        temp[i]=r[i];

    for(i=0;  i< 10-p;i++)  // 将R中从第p个整数开始的整数前移p个位置

       r[i]=r[p+i];

    for(i=0; i<p; i++)      // 将辅助数组中的p个数据放到R中第n-p个数据的后面

       r[10-p+i]=temp[i];

    cout<<"循环左移"<<p<<"位后，数组变换为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

    return 0;

}

•  编程思路3

将数组R循环左移p位后，前p个数一定移动到后面，而后n-p移动到前面，因此可先将数组R逆置，然后再将R中前n-p个元素原地逆置，再将后p个元素原地逆置，如图2所示。

 

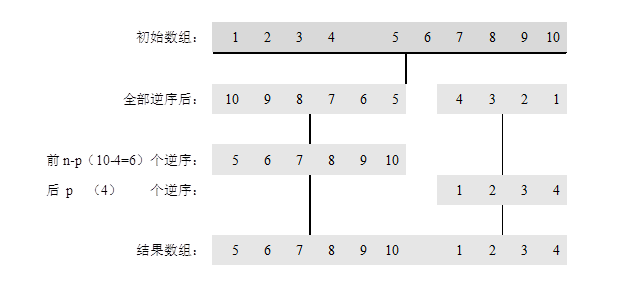
图2  用逆置的方法将数组R中的数据循环移位

为了程序编写简捷，可以将数组R中从begin开始到end结束（包括end）的元素进行逆置的操作写成如下的函数：

void Reverse(int r[],int begin,int end)

{

    int i,temp;

       for(i=0;i<(end-begin+1)/2;i++)

       {

              temp=r[begin+i];  r[begin+i]=r[end-i]; r[end-i]=temp;

       }

}

这样，上述算法中三个Reverse函数的时间复杂度分别为O（n/2）、O（(n-p)/2）和O（p/2），故所设计的算法的时间复杂度为O（n），空间复杂度为O（1）。

• 源程序3

#include <iostream>

using namespace std;

void Reverse(int r[],int begin,int end)

{

    int i,temp;

       for(i=0;i<(end-begin+1)/2;i++)

       {

              temp=r[begin+i];  r[begin+i]=r[end-i]; r[end-i]=temp;

       }

}

int main()

{

    int  r[10]={1,2,3,4,5,6,7,8,9,10};

    int i,p;

    cout<<"请输入需要左移的次数p （0<p<10):";

       cin>>p;

    cout<<"数组初始情况为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

    Reverse(r,0,10-1);       // 全部逆置

       Reverse(r,0,10-p-1);     // 前n-p个元素逆置

       Reverse(r,10-p,10-1);    // 后p个元素逆置

    cout<<"循环左移"<<p<<"位后，数组变换为：";

       for (i = 0; i <10 ; i++)  

         cout<<r[i]<<"  ";

    cout<<endl;

    return 0;

}