我们知道在直角坐标系中,圆的方程可描述为:
X=R*COS(α)
Y=R*SIN(α)
用循环依次取α值为0~2π,计算出X和Y,在canvas画布中将坐标点(X,Y)用线连起来,可绘制出一个圆。编写HTML文件内容如下:
<!DOCTYPE html>
<head>
<title>圆的绘制</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,300);
context.strokeStyle="red";
context.lineWidth=2;
var dig=Math.PI/180;
context.beginPath();
var r=100;
for (var i=0;i<=360;i++)
{
x=200+r*Math.cos(i*dig);
y=150+r*Math.sin(i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas!
</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图1所示的圆。

图1 圆的绘制
1.圆和正弦波合成的花卉图
先在HTML页面中设置一个画布。
<canvas id="myCanvas" width="400" height="300">
</canvas>
再在定义的这块400*300的canvas(画布)上面用循环(0~2π)绘制圆和正弦波合成的花卉图。
绘制图案的基本思想是:将圆的方程与一个正弦波进行迭加,即设立坐标计算公式为:
X=R*COS(α)*(0.5+SIN(6α)/2)
Y=R*SIN(α) *(0.5+SIN(6α)/2)
再用循环依次取α值为0~2π,计算出X和Y,在canvas画布中将坐标点(X,Y)用线连起来,可绘制出一个封闭曲线图形,然后将该图形填充颜色,可得到一个花卉图案。
可编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>圆和正弦波合成的花卉图</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,300);
context.fillStyle="red";
context.strokeStyle="white";
context.lineWidth=2;
var dig=Math.PI/180;
context.beginPath();
var r=100;
for (var i=0;i<=360;i++)
{
c=r*(1/2.0+Math.sin(6*i*dig)/2);
x=200+c*Math.cos(i*dig);
y=150+c*Math.sin(i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas!
</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图2所示的圆和正弦波合成的花卉图。

图2 圆和正弦波合成的花卉图
2.可设置合成方式的圆和正弦波合成花卉图
在上面的代码中,语句“c=r*(1/2.0+Math.sin(6*i*dig)/2);”中的6表示绘制的花卉图案的花瓣数目,0.5(1/2)表示将圆和正弦波合成时,圆所占的比例,如果修改这两个值,将绘制出不同的花卉图案。
我们可以在浏览器窗口中定义一个表单,通过表单可以设置花瓣数目,还可以设置圆和正弦波合成时的比例,这样输入相应参数值后,再单击“确定”按钮绘制合成花卉图案。
编写HTML文件如下。
<!DOCTYPE html>
<head>
<title>可设置合成方式的圆和正弦波合成花卉图</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,500,300);
context.fillStyle="red";
context.strokeStyle="white";
context.lineWidth=2;
var dig=Math.PI/180;
context.beginPath();
var r=100;
var n=eval(document.myForm.petalNum.value);
var a=eval(document.myForm.circle.value);
var b=eval(document.myForm.sineWave.value);
var prop=a/(a+b);
for (var i=0;i<=360;i++)
{
c=r*(prop+(1-prop)*Math.sin(n*i*dig));
x=250+c*Math.cos(i*dig);
y=150+c*Math.sin(i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body>
<form name="myForm">
花瓣数<input type=number name="petalNum" value=6 size=2>
合成比例  圆:正弦波=<input type=number name="circle" value=1 size=2>:<input type=number name="sineWave" value=1 size=2>
<input type=button value="确定" onClick="draw('myCanvas');">
</form><br>
<canvas id="myCanvas" width="500" height="300">您的浏览器不支持canvas!
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在表单的“花瓣数”数字框中输入“20”,“合成比例”对应的两个数字框中输入“1”和“1”,单击“确定”按钮,可以看到在浏览器窗口中绘制出如图3所示的20瓣花卉图案。若在表单的“花瓣数”数字框中输入“8”,“合成比例”对应的两个数字框中输入“2”和“10”,单击“确定”按钮,可以看到在浏览器窗口中绘制出如图4所示的8瓣花卉图案。

图3 20瓣花卉图案
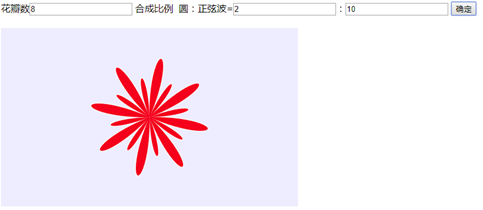
图4 8瓣花卉图案
3.圆和三次谐波合成的花卉图
前面是将圆的方程与一个正弦波进行迭加,若将一个圆与一个三次谐波合成,可设立坐标计算公式为:
X=R*(1+SIN(3*6α)/5)*(0.5+SIN(6α)/2)*COS(α)
Y=R*(1+SIN(3*6α)/5)*(0.5+SIN(6α)/2)*SIN(α)
完整的HTML代码如下。
<!DOCTYPE html>
<head>
<title>圆和三次谐波合成的花卉图</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,400,300);
context.fillStyle="red";
context.strokeStyle="white";
context.lineWidth=2;
var dig=Math.PI/180;
context.beginPath();
var r=100;
for (var i=0;i<=360;i++)
{
b=r+r/5*Math.sin(3*6*i*dig);
c=b*(1/2.0+Math.sin(6*i*dig)/2);
x=200+c*Math.cos(i*dig);
y=150+c*Math.sin(i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas!
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图5所示的圆和三次谐波合成的花卉图。

图5 圆和三次谐波合成的花卉图
若将合成计算式中的(1+SIN(3*6α)/5)改写为(1+SIN(5*6α)/5),也就是将语句“b=r+r/5*Math.sin(3*6*i*dig);”改写为“b=r+r/5*Math.sin(5*6*i*dig);”,再在浏览器中打开修改后的html文件,可以看到在浏览器窗口中绘制出如图6所示的圆和五次谐波合成的花卉图。

图6 圆和五次谐波合成的花卉图
4.圆和三次谐波合成的不同花瓣数的花卉图
在与三次谐波进行合成时,同样可以设置花卉的花瓣数目。可以编写HTML文件如下。
<!DOCTYPE html>
<head>
<title>圆和三次谐波合成不同花瓣数的花卉图</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.fillStyle="red";
context.strokeStyle="white";
context.lineWidth=2;
var dig=Math.PI/180;
context.beginPath();
var r=50;
for (var n=2;n<=10;n++)
{
var offsetx=(n-2)%3*100+50;
var offsety=((n-1)%3!=0?Math.floor((n-1)/3):(n-1)/3-1)*100+50;
for (var i=0;i<=360;i++)
{
b=r+r/5*Math.sin(3*n*i*dig);
c=b*(1/2.0+Math.sin(n*i*dig)/2);
x=offsetx+c*Math.cos(i*dig);
y=offsety+c*Math.sin(i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
context.fill();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas!
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图7所示的圆和三次谐波合成不同花瓣数的花卉图。图中花卉的花瓣数分别为2~9。

图7 圆和三次谐波合成不同花瓣数的花卉图