1.1 六瓣花平移变换
平移变换是指图形从一个位置到另一个位置所作的直线移动。如果要把一个位于P(x,y)的点移到新位置P’(x’,y’),如图1,则只要在原坐标上加上平移距离Tx和Ty即可。
即 x’=x+Tx
y’=y+Ty
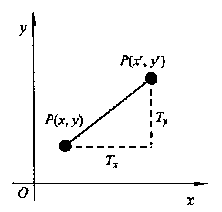
图1 点的平移
生成一个六瓣花型图案的基本数据,通过平移变换绘制8行8列共64个六瓣花型的图案。
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>六瓣花平移变换</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,320,320);
context.strokeStyle="blue";
context.lineWidth=1;
var dig=Math.PI/64;
var x=new Array();
var y=new Array();
var r=40;
// 生成一个六瓣花型图案的基本数据
for (var i=0;i<=128;i++)
{
d=r/2*(0.8+Math.sin(18*i*dig)/5)*1.3;
t=d*(0.5+Math.sin(6*i*dig)/2);
x[i]=t*Math.cos(i*dig);
y[i]=t*Math.sin(i*dig);
}
// 通过平移变换绘制8行8列共64个六瓣花型的图案
for (var row=1;row<=8;row++)
for (var col=1;col<=8;col++)
{
// 计算平移量px和py
px=(2*col-1)/2*r;
py=(2*row-1)/2*r;
for (i=0;i<=128;i++)
{
x1=x[i]+px;
y1=y[i]+py;
if (i==0)
{
context.moveTo(x1,y1);
bx=x1; by=y1;
}
else
context.lineTo(x1,y1);
}
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
}
</script>
</head>
<body onload="draw('myCanvas');">
<canvas id="myCanvas" width="320" height="320">您的浏览器不支持canvas!
</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出64个六瓣花型的图案,如图2所示。

图2 64个六瓣花型的图案
1.2 对称变换
对称变换的公式如下:
x’=ax+by
y’=cx+dy
当a,b,c,d 取不同值时,产生不同的对称变换。
(1)当b=c=0,a=-1,d=1 时,产生相对于y 轴对称的反射图形。
(2)当b=c=0,a=1,d=-1 时,产生相对于x 轴对称的反射图形。
(3)当b=c=0,a=d=-1 时,产生相对于原点对称的反射图形。
(4)当b=c=1,a=d=0 时,产生相对于直线y=x 对称的反射图形。
(5)当b=c=-1,a=d=0 时,产生相对于直线y=-x 对称的反射图形。
各对称变换如图3所示。
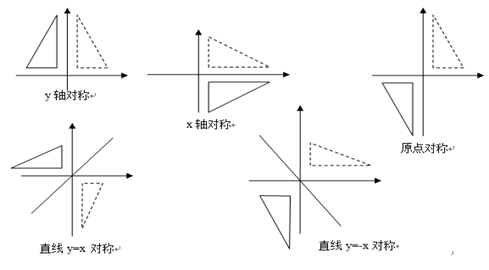
图3 对称变换
在半径为60的圆周上取5个等分点,用这5个点依次首尾连接画5条线,可以绘制出一个正多边形。用这个正多边形为原图,根据选择的方式,进行对称变换。
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>对称变换</title>
<script type="text/javascript">
// 定义保存基本图案数据的数组
var x=new Array(10);
var y=new Array(10);
var dig=2*Math.PI/5;
for (var i=0;i<=5;i++)
{
x[i]=-75+60*Math.sin(i*dig);
y[i]=-75+60*Math.cos(i*dig);
}
function draw()
{
var sele=document.frm.shape.selectedIndex;
var canvas=document.getElementById("myCanvas");
if (canvas==null)
return false;
var context=canvas.getContext('2d');
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
//绘制x轴、y轴(注意:我们不进行旋转,故y轴向下)
context.beginPath();
context.moveTo(0,150);
context.lineTo(285,150);
context.moveTo(150,0);
context.lineTo(150,285);
context.strokeStyle = "blue";
context.stroke();
context.fillStyle = "blue";
context.beginPath();
context.moveTo(285,145);
context.lineTo(295,150);
context.lineTo(285,155);
context.closePath();
context.fill();
context.beginPath();
context.moveTo(145,285);
context.lineTo(150,295);
context.lineTo(155,285);
context.closePath();
context.fill();
context.fillStyle="yellow";
context.strokeStyle="red";
context.lineWidth=1;
context.save();
context.translate(150,150);
context.beginPath();
context.moveTo(x[0],y[0]);
for (n=1;n<=5;n++)
{
context.lineTo(x[n],y[n]);
}
context.closePath();
context.stroke();
context.fill();
context.beginPath();
context.moveTo(x[0],y[0]);
context.lineTo(x[2],y[2]);
context.strokeStyle="black";
context.stroke();
context.fillStyle="red";
context.strokeStyle="yellow";
context.beginPath();
switch(sele)
{
case 1: b=c=0,a=1,d=-1; break;
case 2: b=c=0,a=-1,d=1; break;
case 3: b=c=0,a=d=-1; break;
case 4: b=c=1,a=d=0; break;
case 5: b=c=-1,a=d=0; break;
}
context.moveTo(a*x[0]+b*y[0],c*x[0]+d*y[0]);
for (n=1;n<=5;n++)
{
context.lineTo(a*x[n]+b*y[n],c*x[n]+d*y[n]);
}
context.closePath();
context.stroke();
context.fill();
context.beginPath();
context.moveTo(a*x[0]+b*y[0],c*x[0]+d*y[0]);
context.lineTo(a*x[2]+b*y[2],c*x[2]+d*y[2]);
context.strokeStyle="black";
context.stroke();
context.restore();
}
</script>
</head>
<body>
<form name="frm">对称方式选择:
<select name="shape" onchange="draw();">
<option>--请选择--</option>
<option>X轴对称</option>
<option>Y轴对称</option>
<option>原点对称</option>
<option>直线Y=X对称</option>
<option>直线Y=-X对称</option>
</select>
</form>
<br/>
<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas!</canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中,出现“对称方式选择:”下拉列表框,提供5种对称方式的选择,改变选定的对称方式后,可以绘制出基本图案的相应对称变换图案。整个演示过程录屏后展示如图8所示。

图4 图形的对称变换