例28 直线蛇形阵
问题描述
编写程序,将自然数1、2、…、N2按蛇形方式逐个顺序存入N阶方阵。例如,当N=3和N=4时的直线蛇形阵如下图1所示。
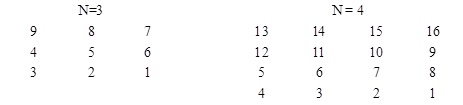
图1 直线蛇形阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的直线蛇形方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
4
输出样例
13 14 15 16
12 11 10 9
5 6 7 8
4 3 2 1
(1)编程思路。
从图1可以看出,直线蛇形阵的构造是从最底行(row=N-1)向最顶行(row=0)进行的。每行的填写在两种方式间切换,一种方式是从右到左顺序(即for(j=n-1;j>=0;j--) )依次递增1填写,称为方式1;另一种方式是从左到右顺序(即for(j=0;j<=n-1;j++) )依次递增1填写,称为方式2。
程序中定义一个变量k来标志这两种方式,k初始值为0,表示采用方式1,当前行按方式1填写完后,改变k的值,使其等于1,表示采用方式2,当前行按方式2填写完后,再改变k的值,使其等于0。
(2)源程序。
#include<stdio.h>
int main()
{
int a[20][20]={0},n;
scanf("%d",&n);
int i,j,k=0,t=1;
for(i=n-1;i>=0;i--) // 遍历行
{
if(k==0) // 从右到左顺序依次递增1存数组元素
{
for(j=n-1;j>=0;j--)
a[i][j]=t++;
k=1;
}
else // 从左到右顺序依次递增1存数组元素
{
for(j=0;j<=n-1;j++)
a[i][j]=t++;
k=0;
}
}
for (i=0;i<n;i++)
{
for (j=0;j<n;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
习题28
28-1 斜线蛇形阵
问题描述
编写程序,将自然数1、2、…、N2按蛇形方式逐个顺序存入N阶方阵。例如,当N=3和N=4时的方阵如下图2所示。

图2 斜线蛇形阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的斜线蛇形方阵。输出时共n行,每行n个数,每个数占4列。
输入样例
5
输出样例
15 16 22 23 25
7 14 17 21 24
6 8 13 18 20
2 5 9 12 19
1 3 4 10 11
(1)编程思路。
观察图2所示的斜线蛇形阵可知,方阵在逐个填数构造的过程中,是沿两种斜线进行的,一种是斜向下,一种是斜向上,如图3(a)所示。
设当前已填入数字的位置的行号为row(row在0~n-1之间),列号为col(col也在0~n-1之间)。若按斜向下填写,则下一位置为row++、col++ ;若按斜向上填写,则下一位置为row--、col--。由于下一位置可能超出方阵的边界,因此有时需要调整。调整有4种情况,下面分别进行说明。
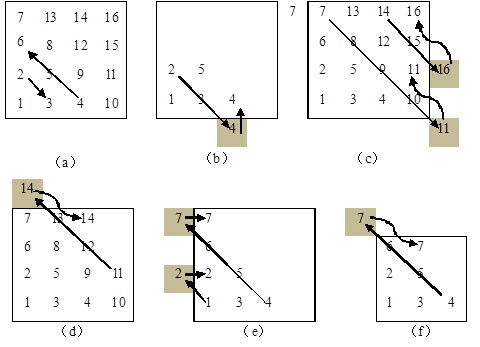
图3 斜线蛇形阵的构造示意图
斜向下填写时,会出现两种情况:
1)超过了底行的位置(即row==n),如图3(b)所示,3填写好后,下一个数4的计算位置越界了,此时进行调整,方法为列col不变,row减1(即 row--)。
2)超过最右列的位置(即col==n),如图3(c)所示,15填写好后,下一个数16的计算位置越界了,此时进行调整,方法为col--、row=row-2。
一种特例,10填写好后,下一个数11的计算位置,行和列都越界了,但处理方法同列越界,因此在程序中应先处理col==n的情况,再处理row==n的情况。这样对于这种特例,由于处理了col==n后,row减了2,不会越界,因此不会再处理row==n的情况。
斜向上填写时,也会出现两种情况:
1)超过了首行的位置(即row==-1),如图3(d)所示,13填写好后,下一个数14的计算位置越界了,此时进行调整,方法为row++、col=col-2。
2)超过最左列的位置(即col==-1),如图3(e)所示,6填写好后,下一个数7的计算位置越界了,此时进行调整,方法为row不变、列号加1(即col++)。
一种特例,在如图3(f)所示的3阶方阵中,6填写好后,下一个数7的计算位置,行和列都越界了,其处理方法同行越界,因此在程序中应先处理row==-1的情况,再处理col==-1的情况。这样对于这种特例,由于处理了row==-1后,col加了2,不会越界,因此不会再处理col==-1的情况。
每次进行越界调整填数后,填数的方向也会发生变化。因此,可设置一个变量up,当up=1时,表示斜向上填数;up=0时,表示斜向下填数。
初始化时,令up=1、row=n-1、col=0、 num=1;在当前位置填上1(即a[row][col]=1),之后进行循环,直到n*n个数填写完毕。循环中,总是先按up的方向,确定下一个位置,然后填上相应的数。例如,1向上到2,越界,调整即可,如图3(e)所示。
(2)源程序。
#include<stdio.h>
int main()
{
int a[20][20]={0},n;
scanf("%d",&n);
int up=1;
int row=n-1;
int col=0;
int num=1;
a[row][col]=num++;
while (num<=n*n)
{
if (up) { row--; col--;}
else { row++; col++;}
if (row==-1) // 超过首行的位置
{ row++; col=col+2; up=1-up; }
if (col==n) // 超过最右列的位置
{ row=row-2; col--; up=1-up; }
if (row==n) // 超过底行的位置
{ row--; up=1-up; }
if (col==-1) // 超过最左列的位置
{ col++; up=1-up; }
a[row][col]=num++;
}
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
printf("%4d",a[i][j]);
printf(" ");
}
return 0;
}
若将程序中的up的初始值设定为0,即开始斜向下填写。重新编译并执行以上程序,则得到如下所示的结果。
5
11 19 20 24 25
10 12 18 21 23
4 9 13 17 22
3 5 8 14 16
1 2 6 7 15
28-2 对称方阵
问题描述
图4所示为两个7阶对称方阵,形象起见,可将(a)方阵称为环形对称方阵,(b)方阵称为三角形对称方阵。

图4 对称方阵
输入格式
两个正整数n(1≤n≤20)和k(k为1或2)。
输出格式
N阶满足要求的对称方阵。若k=1,输出环形对称方阵,k=2,输出三角形对称方阵。输出时共n行,每行n个数,每个数占3列。
输入样例1
5 1
输出样例1
0 1 1 1 0
1 0 2 0 1
1 2 0 2 1
1 0 2 0 1
0 1 1 1 0
输入样例2
7 2
输出样例2
0 1 2 3 2 1 0
1 0 1 2 1 0 1
2 1 0 1 0 1 2
3 2 1 0 1 2 3
2 1 0 1 0 1 2
1 0 1 2 1 0 1
0 1 2 3 2 1 0
(1)编程思路。
1)生成如图4(a)所示的环形对称方阵的方法。
设方阵中元素的行号为row,列号为col。为方便见,row和col均从1开始计。
方阵的主对角线(即row==col)和次对角线(即row+col==n+1)的各元素均赋值“0”。
按两条对角线把方阵可分成上部、左部、右部与下部4个区,如图5所示。
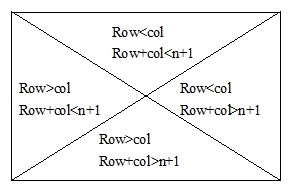
图5 环形对称方阵的四个分区
四个分区的赋值方式为:
上部按行号row赋值,即if (row+col<n+1 && row<col) a[row][col]=row。
下部按表达式n+1-row赋值,即if (row+col>n+1 && row>col) a[row][col]=n+1-row。
左部按列号col赋值,即if (row+col<n+1 && row>col) a[row][col]=col。
右部按表达式n+1-col赋值,即if (row+col>n+1 && row<col) a[row][col]=n+1-col。
2)生成如图4(b)所示的三角形对称方阵的方法。
令m=(n+1)/2,按图6(a)所示分成4个区。
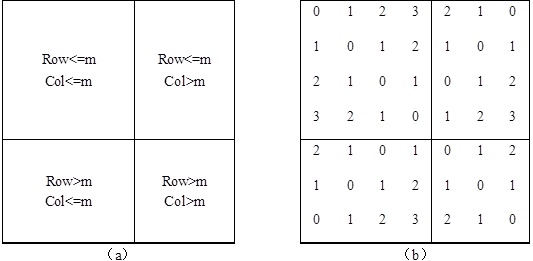
图6 三角形对称方阵的四个分区
仔细分析这个四个分区的元素值与行号、列号的关系,并参照图6(b)所示的7阶对称方阵各元素的值,可归纳出:
左上区(row<=m && col<=m)与右下区(row>m && col>m)参照主对角线赋值:
a[row][col]=abs(row-col) 。
右上区((row<=m && col>m)与左下区(row>m && col<=m)参照次对角线赋值:
a[row][col]= abs(row+col-n-1)。
(2)源程序。
#include <stdio.h>
#include <math.h>
int main()
{
int n,k,row,col,a[21][21]={0};
scanf("%d%d",&n,&k);
if (k==1)
{
for (row=1; row<=n; row++)
for (col=1; col<=n; col++)
{
if (row==col || row+col==n+1)
a[row][col]=0; // 方阵对角线元素赋值
if (row+col<n+1 && row<col)
a[row][col]=row; // 方阵上部元素赋值
if (row+col<n+1 && row>col)
a[row][col]=col; // 方阵左部元素赋值
if (row+col>n+1 && row>col)
a[row][col]=n+1-row; // 方阵下部元素赋值
if (row+col>n+1 && row<col)
a[row][col]=n+1-col; // 方阵右部元素赋值
}
}
else
{
int m=(n+1)/2;
for (row=1; row<=n; row++)
for (col=1; col<=n; col++)
{
if ((row<=m && col<=m) || (row>m && col>m))
a[row][col]=abs(row-col); // 方阵左上部与右下部元素赋值
if ((row<=m && col>m) || (row>m && col<=m))
a[row][col]=abs(row+col-n-1); // 方阵右上部与左下部元素赋值
}
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
printf("%3d",a[i][j]);
printf(" ");
}
return 0;
}
28-3 螺旋下三角阵
问题描述
编写程序,将自然数1、2、…、(1+N)*N/2按螺旋方式逐个顺序存入N阶下三角矩阵。例如,当N=3和N=4时的矩阵如下图7所示。

图7 螺旋下三角阵
输入格式
一个正整数n(1≤n≤20)。
输出格式
N阶满足要求的螺旋下三角阵。输出时每个数占4列。
输入样例
5
输出样例
1 2 3 4 5
12 13 14 6
11 15 7
10 8
9
(1)编程思路
螺旋下三角阵的构造可以看成由向右填充(行号不变、列号加1,即col++)、斜向下填充(row++、col--)和向上填充(行号减1、列号不变,即row--)三个子过程不断交替完成的。
例如,图8所示的3阶螺旋下三角阵可以看成由向右填充(1、2、3),斜向下填充(4、5)和向上填充(6)这3个子过程完成的。4阶螺旋下三角阵可以看成由向右填充(1、2、3、4),斜向下填充(5、6、7)、向上填充(8、9)和向右填充(10)这4个子过程完成的。
n阶螺旋下三角阵可以看成由n个子过程完成,每个子过程为向右填充、斜向下填充和向上填充这三种中的一种,用变量direction来表示,其取值为0、1或2,0表示向右填充,1表示斜向下填充,2表示向上填充。每个子过程结束后,切换填充方向,方式为:
direction=(direction+1)%3;
n个子过程中,第1个子过程填写n个数,第2个子过程填写n-1个数,…,最后一个子过程填写1个数。因此,程序总体写成一个二重循环,描述为:
for (i=n;i>=1;i--)
{
for (j=1;j<=i;j++)
{
按填充方向,填充相应数据
}
direction=(direction+1)%3; // 切换填充方向
}
初始时,注意row=0,col=-1,这样向右col++后,col为0,正好填在第1个位置。
(2)源程序。
#include <stdio.h>
int main()
{
int a[20][20]={0},row,col,i,j,n,num;
int direction=0;
scanf("%d",&n);
row=0; col=-1; num=1;
for (i=n;i>=1;i--)
{
for (j=1;j<=i;j++)
{
switch(direction)
{
case 0:col++;break; // 向右填充
case 1:row++;col--;break; // 斜向下填充
case 2:row--;break; // 向上填充
}
a[row][col]=num++;
}
direction=(direction+1)%3; // 切换填充方向
}
for(row=0;row<n;row++)
{
for(col=0;col<n-row;col++)
printf("%4d",a[row][col]);
printf(" ");
}
return 0;
}