2020软工个人项目作业

北航软工个人项目作业

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
我在这个课程的目标是	学习软件工程相关知识，提高自己团队项目的开发能力
教学班级	005
项目地址	IntersectProject

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	60	60
· Estimate	· 估计这个任务需要多少时间
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	30	120
· Design Spec	· 生成设计文档	15	30
· Design Review	· 设计复审 (和同事审核设计文档)	15	15
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	15	15
· Design	· 具体设计	30	60
· Coding	· 具体编码	90	180
· Code Review	· 代码复审	30	60
· Test	· 测试（自我测试，修改代码，提交修改）	60	90
Reporting	报告
· Test Report	· 测试报告	30	20
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	合计	445	690

解题思路描述

总体思路

本次作业重点在于求解交点个数。通过查阅网上资料，若题目给定任意三条直线不能相交于一点，则可使用动态规划求解。但我们的题目并没有这一条件，那么为了去除所有的重复点，我们就不可避免的需要求出所有交点。最简单的想法是暴力求解，对于输入的集合对象，两两求出交点后用set存储所有交点，最后set中的元素个数即为所有交点数量。对这一想法，可以做出简单的改进，对于一个新加入的几何对象，只需要求出它和之前已经加入进来的几何对象的交点，再把这些交点放入set，相比于最暴力的两两求解，可以减少一半的运算量，本次作业采用这种思路。

• 关于精度问题，由两直线交点坐标公式可知，一个点其实可以用三个整数来表示，这样就不需要担心double带来的精度损失，但是引入圆之后，圆与直线的交点坐标并不满足这种形式，故最终还是采用double进行点的表示。

• 关于可能的改进，事实上，我们每次进行一次交点计算都可以得到一些有用的信息，若充分利用这些信息可以一定程度简化计算。我们知道，若两直线平行，则他们不可能有交点，故可以设计一个以斜率为key的map存储直线，对于新来的斜率为k的直线，无需与map中key为k的直线比较，可以节省一点时间。进一步的，若多条直线交于一点，且它们的交点在新来的直线上，那么新直线也无需与这些直线进行交点计算，因为它们已经不可能产生新的交点。遗憾的是，由于时间原因，这次我并未完成这些优化。

下面讨论各种几何对象的交点求解方式：

直线与直线：直接根据直线交点坐标公式求解,需要注意的是对于平行以及斜率不存在情况的判定

直线与圆：直接联立方程组求解坐标形式未免过于复杂，查阅资料后发现可以借助几何的方法求解

圆与圆：将圆方程化为一般式后，两方程相减即得过两圆交点的直线的方程，从而问题转化为了直线与圆的交点。在求圆与圆的交点之前，需先判断两圆位置关系，可根据以下规则判断：

• d>R+r：两圆外离；两圆的圆心距离之和大于两圆的半径之和

• d=R+r：两圆外切；两圆的圆心距离之和等于两圆的半径之和

• d=R-r：两圆内切；两圆的圆心距离之和等于两圆的半径之差

• d<R-r：两圆内含；两圆的圆心距离之和小于两圆的半径之差

• d<R+r：两园相交；两圆的圆心距离之和小于两圆的半径之和

设计实现过程

总体思路： 程序执行思路为：新读入一个几何对象，判断其类型，之后分别与现有的直线与圆判断位置关系并进行交点运算，将新得出的交点至于set中，结束后将该几何对象也置于线集合或圆集合中。本次涉及的几何对象为直线与圆，故设计两个类分别进行表示。

• 存储结构：

vector<Line> linevec;
vector<Circle> circlevec;
set<Point> pointset;

• line与circle类

class Line {
public:
	// use Ax+By+C=0 to describe a line
	double A, B, C;
	Line(double x1, double y1, double x2, double y2);
	Line(double a, double b, double c);
	Point calintpoint1(Line line1);
};

class Circle {
public:
	double x0, y0, r0;//describe a circle
	Circle(double x0, double y0, double r0);
};

• main函数

	int num = 0;
	while (num < argc) {
		if ((string)argv[num] == "-i") {
			infile.open(argv[num + 1]);	//accept input
		}
		else if ((string)argv[num] == "-o") {
			outfile.open(argv[num + 1]);
		}
		num++;
	}
	int n = 0;
	infile >> n;
	double x1, y1, x2, y2;
	double x0, y0, r0;
	string op;
	int i = 0;
	for (i = 0; i < n; i++) {
		infile >> op;
		if (op == "L") {
			infile >> x1 >> y1 >> x2 >> y2;
			Line line1(x1, y1, x2, y2);
			intersectforline(line1);
		}
		if (op == "C") {
			infile >> x0 >> y0 >> r0;
			Circle circle1(x0, y0, r0);
			intersectforcircle(circle1);
		}
	}

单元测试：

因为本次作业的重点在于求直线交点，故主要对求解两直线交点的方法进行测试，结果均符合预期。如下代码是一个测试样例。

TEST_METHOD(TestMethod10)
		{
			Line line1(0, 1, 1, 5);
			Line line2(0, 3, 1, 10);
			pair<double, double> point;
			point.first = -(double)(2)/3;
			point.second = -(double)(5)/3;
			Assert::AreEqual(line1.calintpoint1(line2).x, point.first);
			Assert::AreEqual(line1.calintpoint1(line2).y, point.second);
		}

性能分析

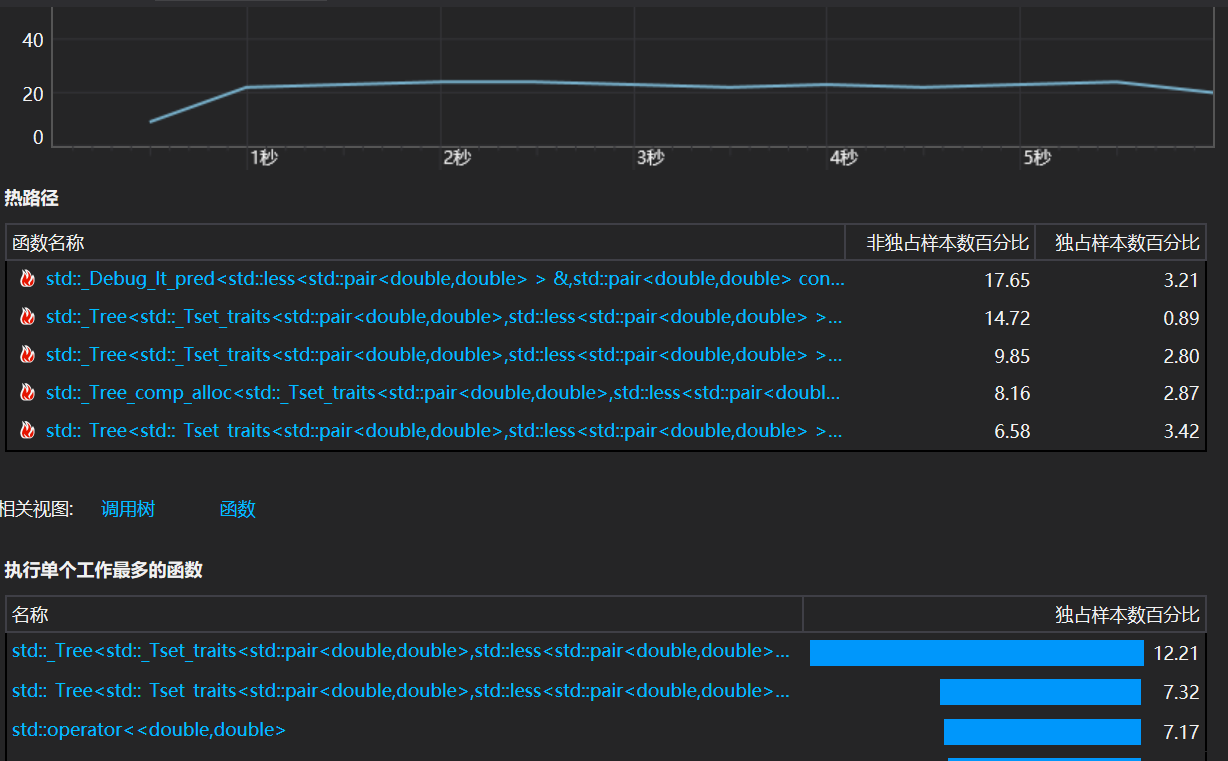
起初，我的直线和点都是通过set进行存储，从图中可以看出，用set容器存储结点时，因为set内部的有序性，导致插入结点时维护红黑树所要付出的代价太大。为了适当减少这部分影响，我选择改用vector容器来完成对于直线和圆的存储，但由于交点的不可重复性，用vector需要去重，当数据量很大时vector应该也要付出相当的代价，故对于交点我依然使用set进行存储。

可以看到，插入交点依然是我程序目前性能的主要瓶颈，但由于设计原因，我目前还没有找到优化的办法。

关键代码说明

• 求两直线的交点

Point Line::calintpoint1(Line line1) {//line and line
	double tmp1 = B * line1.C - line1.B * C;
	double tmp2 = A * line1.B - line1.A * B;
	double tmp3 = line1.A * C - A * line1.C;
	double x = tmp1 / tmp2;
	double y = tmp3 / tmp2;//直线交点坐标公式
	Point point(x, y);
	return point;
}

• 求直线与圆的交点

void calintpoint2(Line line, Circle circle, double dis) {//line and circle
	Line line2(line.B, -line.A, line.A * circle.y0 - line.B * circle.x0);//过圆心的垂线
	Point point = line.calintpoint1(line2);//垂足
	pair<double, double> e;//定义直线的单位向量
	double gougu = sqrt(circle.r0 * circle.r0 - dis * dis);
	e.first = (double)line.B / sqrt(line.A * line.A + line.B * line.B);
	e.second = -(double)line.A / sqrt(line.A * line.A + line.B * line.B);//求直线的单位向量
	Point point1(point.x + e.first * gougu, point.y + e.second * gougu);
	pointset.insert(point1);

	if (dis == circle.r0)//若相切则只有一个交点
		return;

	Point point2(point.x - e.first * gougu, point.y - e.second * gougu);
	pointset.insert(point2);
}

• 直线与现有几何对象求交点过程

void intersectforline(Line line1) {
	//line and line
	vector<Line>::iterator iter1;
	for (iter1 = linevec.begin(); iter1 != linevec.end(); ++iter1)
	{
		if (line1.A * (*iter1).B - (*iter1).A * line1.B == 0) { //parallel
			;
		}
		else {
			Point point = line1.calintpoint1(*iter1);
			pointset.insert(point);
		}
	}
	//line and circle
	vector<Circle>::iterator iter2;
	for (iter2 = circlevec.begin(); iter2 != circlevec.end(); ++iter2)
	{
		double dis = getdistance(line1, *iter2);
		if (dis > (*iter2).r0) {//直线与圆相离
			continue;
		}
		else {
			calintpoint2(line1, (*iter2), dis);
		}
	}
	linevec.push_back(line1);
}

• 圆与现有几何对象求交点过程

void intersectforcircle(Circle circle1) {
	//line and circle
	vector<Line>::iterator iter1;
	for (iter1 = linevec.begin(); iter1 != linevec.end(); ++iter1)
	{
		double dis = getdistance(*iter1, circle1);
		if (dis > circle1.r0) {//直线与圆相离
			continue;
		}
		else {
			calintpoint2(*iter1, circle1, dis);
		}
	}
	//circle and circle
	vector<Circle>::iterator iter2;
	for (iter2 = circlevec.begin(); iter2 != circlevec.end(); ++iter2)
	{
		double d = sqrt((circle1.x0 - (*iter2).x0) * (circle1.x0 - (*iter2).x0) + (circle1.y0 - (*iter2).y0) * (circle1.y0 - (*iter2).y0));
		if (d == 0 || d < fabs(circle1.r0 - (*iter2).r0) || d >(circle1.r0 + (*iter2).r0)) {
			continue;
		}//判断两圆是否有交点

		//求出过两圆交点的直线
		Line line1(2 * ((*iter2).x0 - circle1.x0), 2 * ((*iter2).y0 - circle1.y0), circle1.x0 * circle1.x0 + circle1.y0 * circle1.y0 - 
			(*iter2).x0 * (*iter2).x0 - (*iter2).y0 * (*iter2).y0 + (*iter2).r0 * (*iter2).r0 - circle1.r0 * circle1.r0);
		double dis = getdistance(line1, circle1);
		calintpoint2(line1, circle1, dis);//求出两圆交点
	}
	circlevec.push_back(circle1);
}

相关截图

• 无警告