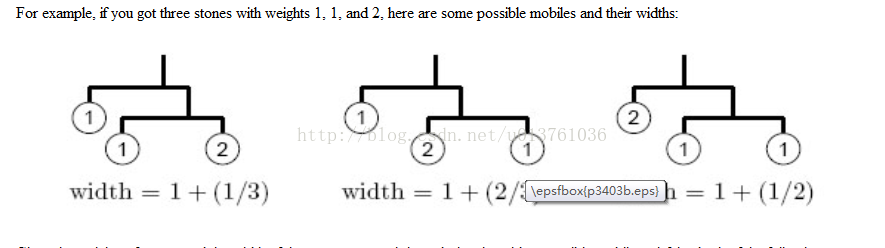
给出房间的宽度r和每个吊坠的重量wi,设计一个尽量宽但宽度不能超过房间宽度的天平,挂着所有挂坠,每个天平的一段要么挂这一个吊坠,要么挂着另一个天平,每个天平的总长度是1,细节我给出题目中的几个图来方便理解:
思路:
敲了将近两个小时,数据比较小,也就是说只要找到解决方法,一般就可以直接AC了,首先我们可以搜索枚举天平的状态,就是总的天平的框架的样子,也就是二叉树的样子,这个地方卡了一会才想出来,我们可以直接枚举当天天平上有的点,每一步搜索是在当前天平上已有的点的叶子节点中两种决策,要么增加一个天平,要么不增加,在别的叶子节点上增加天平,总之当前这一步要在一个叶子节点上增加天平,(想想我们画二叉树的时候是不是这样画的),而且每增加一个天平就会在二叉树上增加一个挂坠的数量,一直增加到测试数据给的吊坠的数量,对于每一个枚举得到的二叉树,我们可以知道他一定是n个叶子节点的二叉树,然后我们用一个全排列(也可以写深搜,用全排列是为了不让代码太多,太乱)给这个叶子附上对应的重量,赋完重量之后我们可以再用深搜来给每个非叶子节点到他做儿子和有儿子的距离求出来,这个比较简单(不会可以直接看下面代码),求完距离之后可以用深搜遍历没一条路径,树根的坐标是0,然后往左就-,往右就+得到一个最大和最小的坐标,然后根据坐标差来更新最优值,这个题目我写了三个深搜,一个全排列AC的,感觉实现的有点麻烦,但不知道有没有更省事的,目前百度不到,还有就是有一个比较坑人的地方就是当吊坠只有一个的时候直接输出0,不是-1。
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 3000
using namespace std;
typedef struct
{
double ll ,rr ,ww;
int mk;
}NODE;
NODE node[N];
int Now[N] ,n ,nn;
double num[10] ,r ,Ans;
double minn ,maxx;
double DFSlr(int now)
{
if(node[now].mk) return node[now].ww;
double lsum = DFSlr(now * 2);
double rsum = DFSlr(now * 2 + 1);
node[now].ll = rsum / (lsum + rsum);
node[now].rr = lsum / (lsum + rsum);
return lsum + rsum;
}
void DFSmm(double v ,int now)
{
if(node[now].mk)
{
if(minn > v) minn = v;
if(maxx < v) maxx = v;
return;
}
DFSmm(v - node[now].ll ,now * 2);
DFSmm(v + node[now].rr ,now * 2 + 1);
}
void DFS(int sw ,int sumnode)
{
if(sw == n)
{
int tmpyz[10] ,nowid = 0;
for(int i = 1 ;i <= sumnode ;i ++)
if(node[Now[i]].mk) tmpyz[++nowid] = Now[i];
for(int i = 1 ;i <= nn+1 ;i ++)
{
for(int j = 1 ;j <= n ;j ++)
node[tmpyz[j]].ww = num[j];
DFSlr(1);
maxx = -100000 ,minn = 100000;
DFSmm(0 ,1);
if(maxx - minn <= r)
{
if(Ans < maxx - minn)
Ans = maxx - minn;
}
next_permutation(num + 1 ,num + n + 1);
}
return;
}
for(int i = 1 ;i <= sumnode ;i ++)
{
if(node[Now[i]].mk)
{
node[Now[i]].mk = 0;
node[Now[i]*2].mk = 1;
node[Now[i]*2+1].mk = 1;
Now[sumnode+1] = Now[i]*2;
Now[sumnode+2] = Now[i]*2+1;
DFS(sw + 1 ,sumnode + 2);
node[Now[i]].mk = 1;
node[Now[i]*2].mk = 0;
node[Now[i]*2+1].mk = 0;
}
}
}
int main ()
{
int t ,i;
scanf("%d" ,&t);
while(t--)
{
scanf("%lf" ,&r);
scanf("%d" ,&n);
for(nn = i = 1 ;i <= n ;i ++)
{
scanf("%lf" ,&num[i]);
nn *= i;
}
if(n == 1)
{
printf("0 ");
continue;
}
memset(node ,0 ,sizeof(node));
Now[1] = 1 ,Ans = -1;
node[1].mk = 1;
DFS(1 ,1);
printf("%.16lf " ,Ans);
}
return 0;
}