整形与浮点型

01. 整形

Go 语言中，整数类型可以再细分成10个类型，

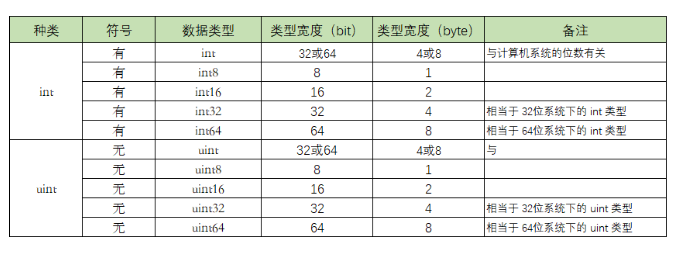
int 和 uint 的区别就在于一个 u，有 u 说明是无符号，没有 u 代表有符号。

解释这个符号的区别

以 int8 和 uint8 举例，8 代表 8个bit，能表示的数值个数有 2^8 = 256。

uint8 是无符号，能表示的都是正数，0-255，刚好256个数。

int8 是有符号，既可以正数，也可以负数，那怎么办？对半分呗，-128-127，也刚好 256个数。

int8 int16 int32 int64 这几个类型的最后都有一个数值，这表明了它们能表示的数值个数是固定的。

而 int 没有并没有指定它的位数，说明它的大小，是可以变化的，那根据什么变化呢？

• 当你在32位的系统下，int 和 uint 都占用 4个字节，也就是32位。

• 若你在64位的系统下，int 和 uint 都占用 8个字节，也就是64位。

出于这个原因，在某些场景下，你应当避免使用 int 和 uint ，而使用更加精确的 int32 和 int64，比如在二进制传输、读写文件的结构描述（为了保持文件的结构不会受到不同编译目标平台字节长度的影响）

不同进制的表示方法

出于习惯，在初始化数据类型为整形的变量时，我们会使用10进制的表示法，因为它最直观，比如这样，表示整数10.

var num int = 10

不过，你要清楚，你一样可以使用其他进制来表示一个整数，这里以比较常用的2进制、8进制和16进制举例。

2进制：以0b或0B为前缀

var num01 int = 0b1100

8进制：以0o或者 0O为前缀

var num02 int = 0o14

16进制：以0x 为前缀

var num03 int = 0xC

下面用一段代码分别使用二进制、8进制、16进制来表示 10 进制的数值：12

package main

import (
    "fmt"
)

func main() {
    var num01 int = 0b1100
    var num02 int = 0o14
    var num03 int = 0xC

    fmt.Printf("2进制数 %b 表示的是: %d 
", num01, num01)
    fmt.Printf("8进制数 %o 表示的是: %d 
", num02, num02)
    fmt.Printf("16进制数 %X 表示的是: %d 
", num03, num03)
}
输出如下

2进制数 1100 表示的是: 12 
8进制数 14 表示的是: 12 
16进制数 C 表示的是: 12 

以上代码用过了 fmt 包的格式化功能，你可以参考这里去看上面的代码

%b    表示为二进制
%c    该值对应的unicode码值
%d    表示为十进制
%o    表示为八进制
%q    该值对应的单引号括起来的go语法字符字面值，必要时会采用安全的转义表示
%x    表示为十六进制，使用a-f
%X    表示为十六进制，使用A-F
%U    表示为Unicode格式：U+1234，等价于"U+%04X"

 

02. 浮点型

浮点数类型的值一般由整数部分、小数点“.”和小数部分组成。

其中，整数部分和小数部分均由10进制表示法表示。不过还有另一种表示方法。那就是在其中加入指数部分。指数部分由“E”或“e”以及一个带正负号的10进制数组成。比如，3.7E-2表示浮点数0.037。又比如，3.7E+1表示浮点数37。

有时候，浮点数类型值的表示也可以被简化。比如，37.0可以被简化为37。又比如，0.037可以被简化为.037。

有一点需要注意，在Go语言里，浮点数的相关部分只能由10进制表示法表示，而不能由8进制表示法或16进制表示法表示。比如，03.7表示的一定是浮点数3.7。

float32 和 float64

Go语言中提供了两种精度的浮点数 float32 和 float64。

float32，也即我们常说的单精度，存储占用4个字节，也即4*8=32位，其中1位用来符号，8位用来指数，剩下的23位表示尾数

float64，也即我们熟悉的双精度，存储占用8个字节，也即8*8=64位，其中1位用来符号，11位用来指数，剩下的52位表示尾数

那么精度是什么意思？有效位有多少位？

精度主要取决于尾数部分的位数。

对于 float32（单精度）来说，表示尾数的为23位，除去全部为0的情况以外，最小为2^-23，约等于1.19*10^-7，所以float小数部分只能精确到后面6位，加上小数点前的一位，即有效数字为7位。

同理 float64（单精度）的尾数部分为 52位，最小为2^-52，约为2.22*10^-16，所以精确到小数点后15位，加上小数点前的一位，有效位数为16位。

通过以上，可以总结出以下几点：

1. float32 和 float64 可以表示的数值很多

浮点数类型的取值范围可以从很微小到很巨大。浮点数取值范围的极限值可以在 math 包中找到：

• 常量 math.MaxFloat32 表示 float32 能取到的最大数值，大约是 3.4e38；

• 常量 math.MaxFloat64 表示 float64 能取到的最大数值，大约是 1.8e308；

• float32 和 float64 能表示的最小值分别为 1.4e-45 和 4.9e-324。

2. 数值很大但精度有限

人家虽然能表示的数值很大，但精度位却没有那么大。

• float32的精度只能提供大约6个十进制数（表示后科学计数法后，小数点后6位）的精度

• float64的精度能提供大约15个十进制数（表示后科学计数法后，小数点后15位）的精度

这里的精度是什么意思呢？

比如 10000018这个数，用 float32 的类型来表示的话，由于其有效位是7位，将10000018 表示成科学计数法，就是 1.0000018 * 10^7，能精确到小数点后面6位。

此时用科学计数法表示后，小数点后有7位，刚刚满足我们的精度要求，意思是什么呢？此时你对这个数进行+1或者-1等数学运算，都能保证计算结果是精确的

import "fmt"
var myfloat float32 = 10000018
func main()  {
    fmt.Println("myfloat: ", myfloat)
    fmt.Println("myfloat: ", myfloat+1)
}
输出如下

myfloat:  1.0000018e+07
myfloat:  1.0000019e+07

上面举了一个刚好满足精度要求数据的临界情况，为了做对比，下面也举一个刚好不满足精度要求的例子。只要给这个数值多加一位数就行了。

换成 100000187，同样使用 float32类型，表示成科学计数法，由于精度有限，表示的时候小数点后面7位是准确的，但若是对其进行数学运算，由于第八位无法表示，所以运算后第七位的值，就会变得不精确。

这里我们写个代码来验证一下，按照我们的理解下面 myfloat01 = 100000182 ，对其+5 操作后，应该等于 myfloat02 = 100000187，

import "fmt"

var myfloat01 float32 = 100000182
var myfloat02 float32 = 100000187

func main() {
    fmt.Println("myfloat: ", myfloat01)
    fmt.Println("myfloat: ", myfloat01+5)
    fmt.Println(myfloat02 == myfloat01+5)
}

但是由于其类型是 float32，精度不足，导致最后比较的结果是不相等（从小数点后第七位开始不精确）

myfloat:  1.00000184e+08
myfloat:  1.0000019e+08
false

由于精度的问题，就会出现这种很怪异的现象，myfloat == myfloat +1 会返回 true 。