---恢复内容开始---
Surround the Trees |
| Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) |
| Total Submission(s): 166 Accepted Submission(s): 81 |
| |
|
Problem Description
There are a lot of trees in an area. A peasant wants to buy a
rope to surround all these trees. So at first he must know the minimal
required length of the rope. However, he does not know how to calculate
it. Can you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line. 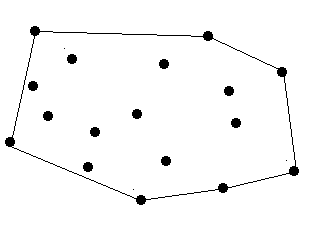 There are no more than 100 trees. |
|
Input
The input contains one or more data sets. At first line of each
input data set is number of trees in this data set, it is followed by
series of coordinates of the trees. Each coordinate is a positive
integer pair, and each integer is less than 32767. Each pair is
separated by blank.
Zero at line for number of trees terminates the input for your program. |
|
Output
The minimal length of the rope. The precision should be 10^-2. |
|
Sample Input
9 12 7 24 9 30 5 41 9 80 7 50 87 22 9 45 1 50 7 0 |
|
Sample Output
243.06 |
|
Source
Asia 1997, Shanghai (Mainland China)
|
题意:求凸包
当点数=1、2、3时分类讨论
其余的求凸包,我用的是极角排序(按叉积排),跑的慢啊。。
推荐网站
1 #include <cmath> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <cstdlib> 6 using namespace std; 7 8 typedef double dd; 9 const int maxn=110; 10 const dd eps=1E-8; 11 struct point 12 { 13 dd x,y; 14 }; 15 point p[maxn],st[maxn]; 16 int n,cnt; 17 dd t,ans,x[maxn],y[maxn],mx,my; 18 19 20 void close() 21 { 22 exit(0); 23 } 24 25 int dblcmp(dd t) 26 { 27 if (fabs(t)<eps) 28 return 0; 29 if (t<0) return -1; 30 else return 1; 31 } 32 33 dd dist(point a,point b) 34 { 35 x[1]=fabs(a.x-b.x); 36 y[1]=fabs(a.y-b.y); 37 return (x[1]*x[1]+y[1]*y[1]); 38 } 39 40 dd mul(point a,point b,point c) 41 { 42 x[1]=b.x-a.x; y[1]=b.y-a.y; 43 x[2]=c.x-a.x; y[2]=c.y-a.y; 44 return (x[1]*y[2]-y[1]*x[2]); 45 } 46 47 bool cmp(point a,point b) 48 { 49 dd t=mul(st[1],a,b); 50 int j=dblcmp(t); 51 if (j==0) //共线 52 return dist(a,st[1])<dist(b,st[1]); 53 if (j==1) 54 return true; 55 else 56 return false; 57 return false; 58 } 59 60 bool judge(point a,point b,point c) 61 { 62 dd t=mul(c,b,a); 63 int j=dblcmp(t); 64 //j==1 顺时针 65 if (j==0) return true; //gong xian de ye bu yao 66 if (j==1) return false; 67 else return true; 68 } 69 void work() 70 { 71 ans=0; 72 if (n==1) {ans=0;return;} 73 if (n==2) {ans=sqrt(dist(p[1],p[2]));return;} 74 if (n==3) {ans=sqrt(dist(p[1],p[2])) + sqrt(dist(p[2],p[3])) + sqrt(dist(p[1],p[3]));return;} 75 mx=p[1].x; 76 my=p[1].y; 77 for (int i=1;i<=n;i++) 78 { 79 if ( (my==p[i].y && mx>p[i].x) || my>p[i].y) 80 { 81 mx=p[i].x; 82 my=p[i].y; 83 } 84 } 85 st[1].x=mx; 86 st[1].y=my; 87 sort(p+1,p+n+1,cmp); 88 st[2].x=p[2].x; 89 st[2].y=p[2].y; 90 cnt=2; 91 for (int i=3;i<=n;i++) 92 { 93 while (judge(p[i],st[cnt],st[cnt-1])) 94 cnt--; 95 cnt++; 96 st[cnt].x=p[i].x; 97 st[cnt].y=p[i].y; 98 } 99 for (int i=2;i<=cnt;i++) 100 ans+=sqrt(dist(st[i],st[i-1])); 101 ans+=sqrt(dist(st[cnt],st[1])); 102 } 103 104 void init() 105 { 106 while (scanf("%d",&n)!=EOF) 107 { 108 if (n==0) close(); 109 for (int i=1;i<=n;i++) 110 { 111 scanf("%lf %lf",&p[i].x,&p[i].y); 112 } 113 work(); 114 printf("%.2lf ",ans); 115 } 116 } 117 118 int main () 119 { 120 init(); 121 close(); 122 return 0; 123 }
http://blog.chinaunix.net/uid-22263887-id-1778926.html
http://www.cnblogs.com/Booble/archive/2011/03/10/1980089.html#2065991
http://blog.csdn.net/javasui/article/details/6759777
http://blog.sina.com.cn/s/blog_87cb8e680100svnd.html
http://blog.chinaunix.net/uid-22263887-id-1778926.html
http://www.cnblogs.com/devymex/archive/2010/08/09/1795392.html