一,插入排序
插入排序基本思想:
在一个已经有序的序列里插入新的元素,直到有序序列包含所有被排序元素。
例子:

代码实现:

void InsertSort(vector<int> &v) { for(int i = 1;i < v.size(); ++i)//i表示有序集合里的元素数目和待插入元素下标 { for(int j = i; j > 0 && v[j-1] > v[j]; --j) { int temp = v[j-1]; v[j-1] = v[j]; v[j] = temp; } } }
时间复杂度为O(N^2)
空间复杂度为O(1)
插入排序在小规模数据时或者基本有序时比较高效。
二,希尔排序
希尔排序基本思想:
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。本质上是分组插入排序。
例子:
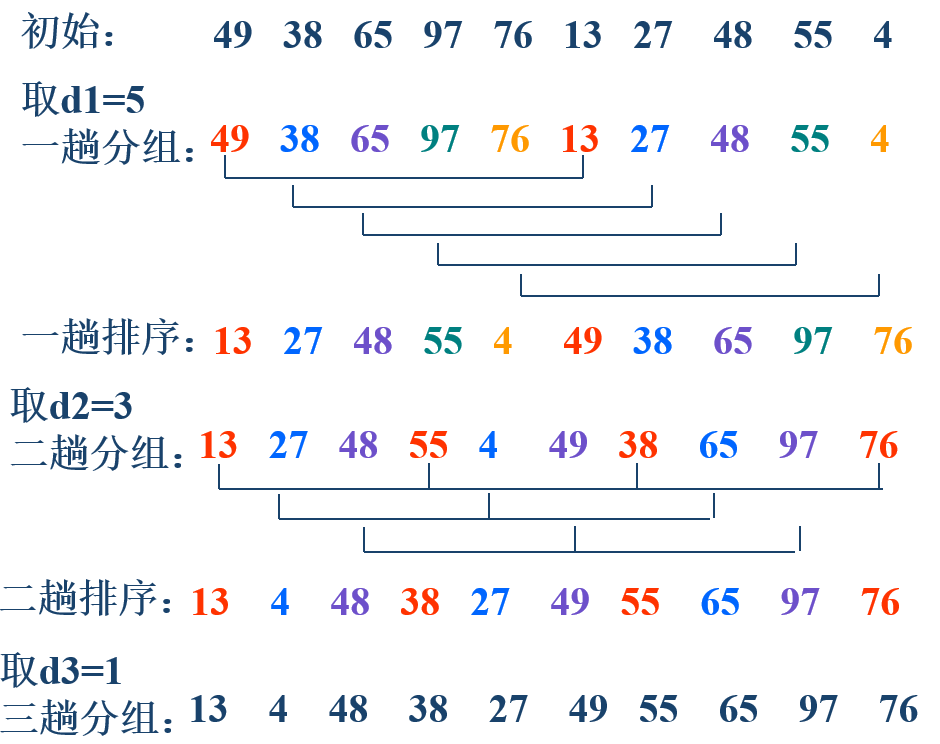
在取增量d的时候一般有以下要求:
①最后一次排序d = 1;
②每次取的d并不包含处1以外的公因子;
③采用缩小增量法,d的取值逐步缩小。
代码实现:

void ShellSort(vector<int> &v) { int k = 0; int t = v.size() - 1; int delta = 2*t - k - 1;//有研究表明,delta取2*t-k-1时时间复杂度可达O(N^1.5) for(k = 0;k < v.size(); ++k) { delta = (2*t-k-1) == t?(2*t-k-1):1;//最后一次delta要取1 for(int i = 0; i < v.size()-delta; ++i) { if(v[i] > v[i+delta]) { int temp = v[i]; v[i] = v[i+delta]; v[i+delta] = temp; } } } }
希尔排序delta开始会很大,所以该排序不稳定。
希尔排序的复杂度与delta相关:
{1,2,4,8,...}使用这个增量序列的时间复杂度(最坏情形)是O(N^2)
代码中所给序列的时间复杂度时O(N^1.5)
空间复杂度为O(1)
希尔排序为插入排序的一种优化,其适用范围为:大规模且无序的数据。
三,冒泡排序
冒泡排序基本思想:
将第一个记录的关键字与第二个记录的关键字进行比较,若逆序则交换;然后比较第二个记录与第三个记录;依次类推,直至第n-1个记录和第n个记录比较为止——第一趟冒泡排序,结果关键字最大的记录被安置在最后一个记录上。
对前n-1个记录进行第二趟冒泡排序,结果使关键字次大的记录被安置在第n-1个记录位置。重复上述过程,直到在一趟排序过程中没有进行过交换操作”为止。
例子:
代码实现:

void BubbleSort(vector<int> &v) { for(int i = 0; i < v.size(); ++i) { for(int j = 0;j < v.size() - i; ++j) { if(v[j] < v[j-1]) { int temp = v[j]; v[j] = v[j-1]; v[j-1] = temp; } } } }
时间复杂度为O(N^2)
空间复杂度为O(1)
冒泡排序是稳定的排序算法。
四,快速排序
快速排序基本思想:
快速排序的本质是分治法。从数列中挑出一个元素,称为 “基准”(pivot) 分区(partition):将序列分区,使所有元素比基准值小的放在基准前面,所有元素比基准值大的放在基准的后面(相等的数可以到任一边)(Divide) 排序:递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序(Conquer)。每次递归都会把基准放在正确的位置,即每次递归都排好一个元素,并将小于这个元素的放左边,大于这个元素的放右边。
例子:
记low为起始位置,high为末位置。基准一般取R[low],R[high],R[(low+high)/2]处于中间大小的数。这里叙述方便,直接取R[0]为基准。
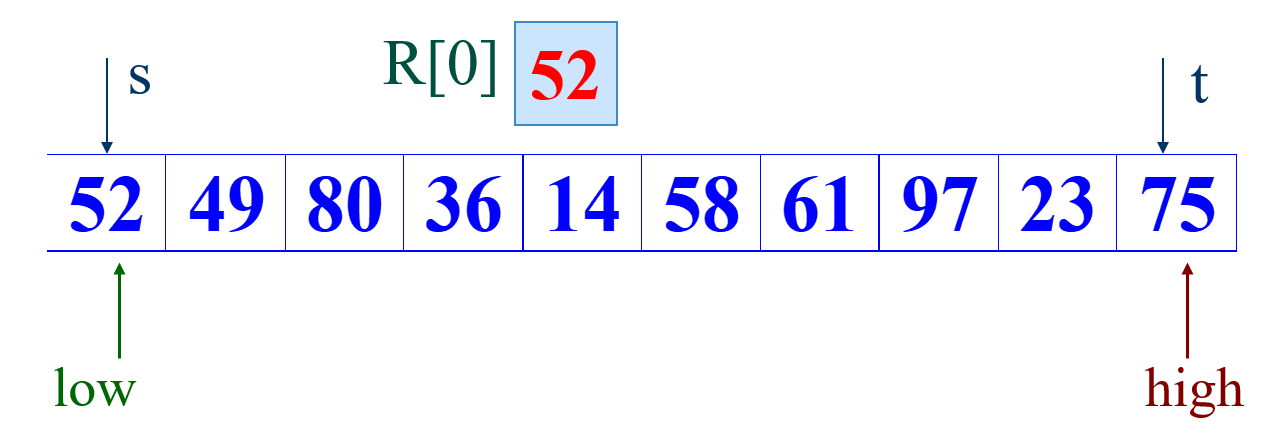
①首先从后半部分开始,如果扫描到的值大于基准数据就让high减1,如果发现有元素比该基准数据的值小,就将high位置的值赋值给low位置 。
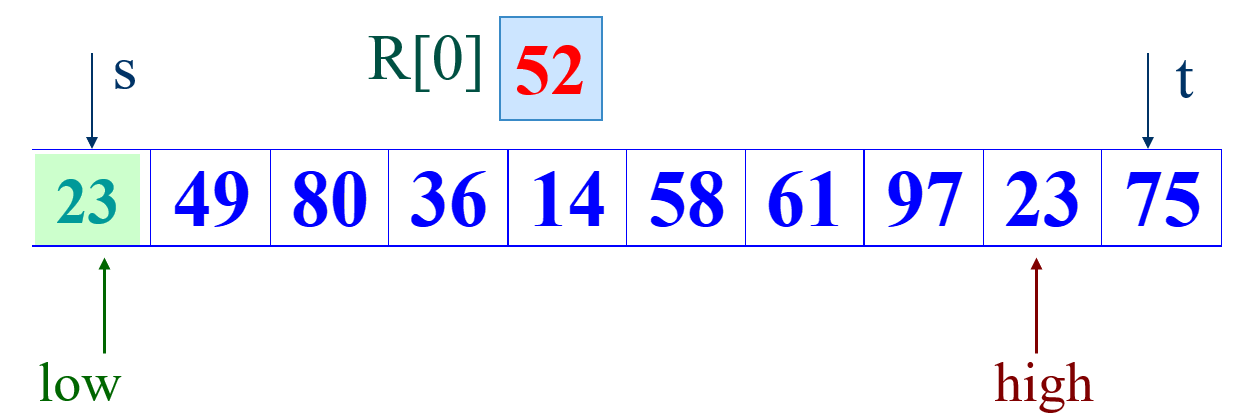
②然后开始从前往后扫描,如果扫描到的值小于基准数据就让low加1,如果发现有元素大于基准数据的值,就再将low位置的值赋值给high位置的值,指针移动并且数据交换后的结果如下:
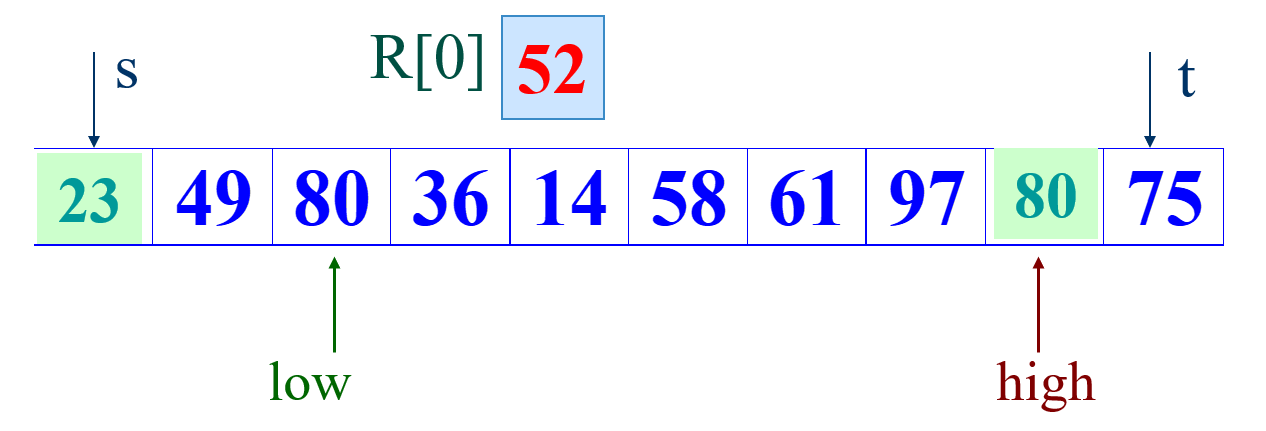
③继续进行以上步骤,直到low >= high 停止扫描,此时基准R[0]处于正确的位置上。
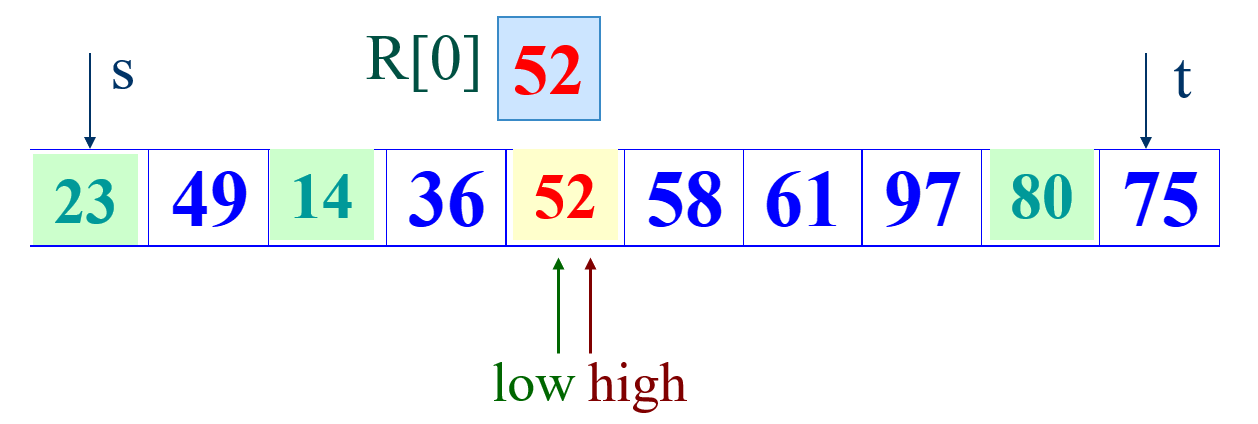
④然后递归的处理左子序列和右子序列。
代码实现:

int Parition(vector<int>&v,int low,int high) { int ref = v[low]; if(low < high) { while(low < high) { while(low < high && v[high] >= ref) { --high; } v[low] = v[high]; while(low < high && v[low] <= ref) { ++low; } v[high] = v[low]; } v[low] = ref; } return low; } void QSort(vector<int>&v,int low,int high) { if(low < high) { int index = Parition(v,low,high); QSort(v,low,index-1); QSort(v,index+1,high); } } void QuickSort(vector<int>&v) { QSort(v,0,v.size()-1); }
时间复杂度为O(NlogN)
空间复杂度为最优的是O(logN),最差的为O(N)
不稳定。
五,简单选择排序
简单选择排序基本思想:
首先通过n-1次关键字比较,从n个记录中找出关键字最小的记录,将它与第一个记录交换;
再通过n-2次比较,从剩余的n-1个记录中找出关键字次小的记录,将它与第二个记录交换;
重复上述操作,共进行n-1趟排序后,排序结束。
例子:
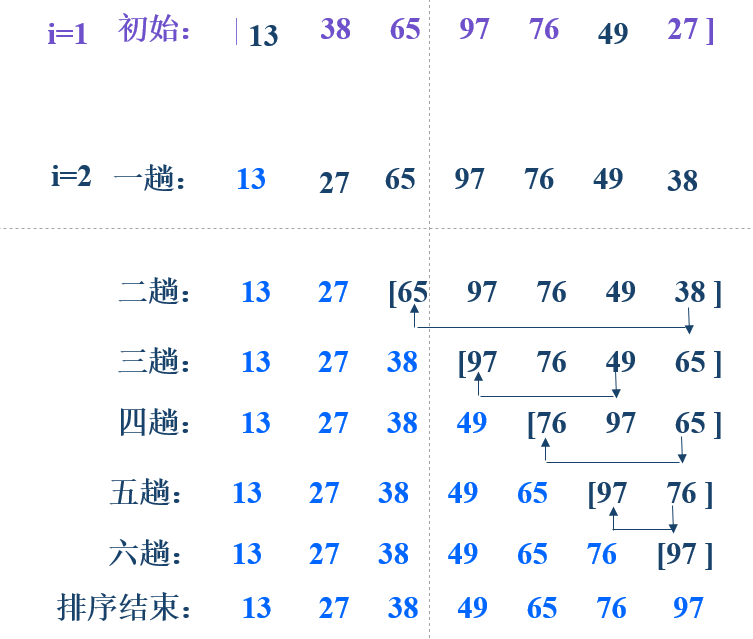
代码实现:

void SelectSort(vector<int>& v) { for(int i = 0; i < v.size(); ++i) { int MIN = v[i],pos = i;; for(int j = i; j < v.size(); ++j) { if(MIN > v[j]) { MIN = v[j]; pos = j; } } v[pos] = v[i]; v[i] = MIN; } }
时间复杂度为O(N^2)
空间复杂度为O(1)
不稳定,交换过程中可能发生相同数字的次序颠倒。
六,堆排序
堆排序基本思想:
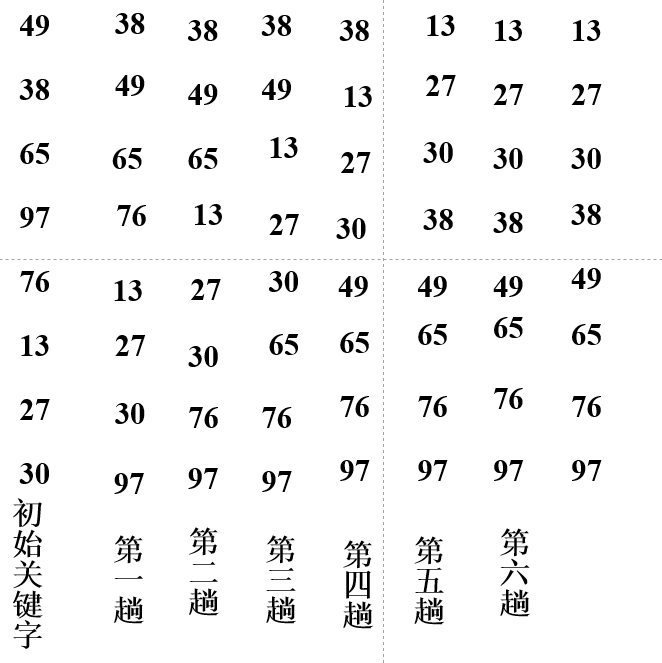
堆是一个具有这样性质的完全二叉树:每个非终端结点(记录)的关键字大于等于(小于等于)它的孩子结点的关键字。堆排序是利用堆的特性对记录序列进行排序的一种排序方法。将无序序列建成一个堆,得到关键字最小(或最大)的记录;输出堆顶的最小(大)值后,使剩余的n-1个元素重又建成一个堆,则可得到n个元素的次小值;重复执行,得到一个有序序列。因为堆是完全二叉树,所以我们可以用数组来储存。只要将需要排序的数组建立成堆,然后每次取出根结点,就把剩下的结点调整成堆;再取出根结点,如此下去,最后便能得到排好序的数据。
例子:
建堆:
给定需要排序的6个数字:

①保证[0,0]范围内是个最大堆,12本身是个堆。
②保证[0,1]范围内是个最大堆,因为34 > 12,12在34的父节点上,所以需要调换12和34

③再保证[0,3]内是个最大堆,12 54都是34的儿子,所以调换34和54
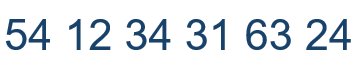
④重复以上步骤,直到[0,n-1]都是个最大堆
建堆结果是:

调整堆并排序:
成为堆以后那么heap[0]一定是该组数的最大值/最小值(这里建的是最大堆,所以heap[0]是最大值)。
①交换63和24,已知63是最大值,则63在排序后的正确位置上,我们假装数组只有n-1个数,把63踢出去。

②然后对[0,n-2]的所以数据进行调整,挑24左右儿子最大的与其比较,54 > 24,所以交换位置。
然后12和31是交换位置后的24的左右儿子,又因为31 > 24交换24,31。

这已经是一个最大堆了,将54和24交换位置(首位交换),54处在正确的位置上。

继续重复上述过程,直到每个数都排好。
代码实现:

void GetHeap(vector<int>& v)//将数组v调整为最大堆 { for(int i = 0; i < v.size(); ++i) { int CurrentIndex = i;//新插入的结点 int Father = (CurrentIndex - 1) / 2; while(v[CurrentIndex] > v[Father]) { int temp = v[CurrentIndex]; v[CurrentIndex] = v[Father]; v[Father] = temp; CurrentIndex = Father; Father = (CurrentIndex - 1) / 2; } } } void AdjustHeap(vector<int>& v,int index,int size)//交换首尾元素后调整最大堆 { int right = 2*index + 2; int left = 2*index + 1; while(left < size) { int LargestIndex; if(v[left] < v[right] && right < size) { LargestIndex = right; } else { LargestIndex = left; } if(v[index] > v[LargestIndex]) { LargestIndex = index; } if(index == LargestIndex) { break; } int temp = v[LargestIndex]; v[LargestIndex] = v[index]; v[index] = temp; index = LargestIndex; left = 2*index + 1; right = 2*index + 2; } } void HeapSort(vector<int>& v) { GetHeap(v); int size = v.size(); while(size > 1) { int temp = v[0]; v[0] = v[size - 1]; v[size - 1] = temp; --size; AdjustHeap(v,0,size); } }
时间复杂度为O(NlogN)
空间复杂度为O(1)
不稳定。
七,归并排序
归并排序基本思想:
归并——将两个或两个以上的有序表组合成一个新的有序表,叫归并。
2-路归并排序:将两个位置相邻的记录有序子序列归并为一个记录的有序序列。
如果记录无序序列 R[s..t] 的两部分 R[s...(s+t)/2] 和 R[(s+t)/2+1..t] 分别按关键字有序, 则很容易将它们归并成整个记录序列是一个有序序列。具体看例子。
例子:
对一个序列不断递归(分治法),然后两两归并并排序。

代码实现:

void MergeArray(vector<int> &v, int left, int mid, int right, int temp[])//归并并排序 { int i = left,j = mid+1; int n = mid,m = right; int k = 0; while(i <= n && j <= m) { if(v[i] < v[j]) { temp[k++] = v[i++]; } else { temp[k++] = v[j++]; } } while(i <= n) { temp[k++] = v[i++]; } while(j <= m) { temp[k++] = v[j++]; } for(int i = 0; i < k; ++i) { v[left+i] = temp[i]; } } void Divide(vector<int>& v,int left,int right,int temp[])//分治 { if(left < right) { int mid = (left+right)/2; Divide(v,left,mid,temp); Divide(v,mid+1,right,temp); MergeArray(v,left,mid,right,temp); } } bool MergeSort(vector<int>& v) { int* temp = new int[v.size()]; if(temp == NULL) { return false; } Divide(v,0,v.size()-1,temp); delete [] temp; return true; }
时间复杂度非常稳定,最好和最差都是O(NlogN)
空间复杂度为O(N) (new了一个大小为n的数组)
