1061: [Noi2008]志愿者招募
Time Limit: 20 Sec Memory Limit: 162 MBSubmit: 5931 Solved: 3566
[Submit][Status][Discuss]
Description
申奥成功后,布布经过不懈努力,终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难
题:为即将启动的奥运新项目招募一批短期志愿者。经过估算,这个项目需要N 天才能完成,其中第i 天至少需要
Ai 个人。 布布通过了解得知,一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天,招募费用
是每人Ci 元。新官上任三把火,为了出色地完成自己的工作,布布希望用尽量少的费用招募足够的志愿者,但这
并不是他的特长!于是布布找到了你,希望你帮他设计一种最优的招募方案。
Input
第一行包含两个整数N, M,表示完成项目的天数和可以招募的志愿者的种类。 接下来的一行中包含N 个非负
整数,表示每天至少需要的志愿者人数。 接下来的M 行中每行包含三个整数Si, Ti, Ci,含义如上文所述。为了
方便起见,我们可以认为每类志愿者的数量都是无限多的。
Output
仅包含一个整数,表示你所设计的最优方案的总费用。
Sample Input
3 3
2 3 4
1 2 2
2 3 5
3 3 2
2 3 4
1 2 2
2 3 5
3 3 2
Sample Output
14
HINT
1 ≤ N ≤ 1000,1 ≤ M ≤ 10000,题目中其他所涉及的数据均 不超过2^31-1。
题解:单纯形裸题,直接上模板即可;(单纯形,后面我会更新讲解的Orz)
设某天需要 第xi 个志愿者的数量,记 mij 表示第 i 天第 j个志愿者是否能工作,则它们需要满足如下条件:
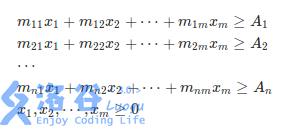
于是所需费用即 C1x1+C2x2+⋯+Cmxm,需要令它最小化。
可以看出,这是一个线性规划问题。
由于它是最小化型线性规划,不是标准形式的。因此,可以利用线性规划对偶定理 (证明可以百度等,比如这里) 将其转化为一个最大化型线性规划:
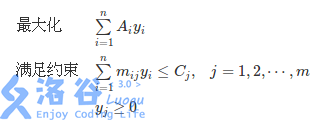
由于 Ci 都是 q 0≥0 的整数,于是上面的线性规划就有基本解 (零解)。于是写个最单纯的单纯形法就可以了 (连 init() 都不用写~)。
具体地过程,就是寻找大于 00 的非基 (自由) 变量转化成基变量,然后转轴 (注意代码实现时和 Gauss 消元的区别),最后得到的就是最小花费。
参考代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define clr(a,b) memset(a,b,sizeof a) 4 #define lowbit(x) x&-x 5 typedef long long ll; 6 const int INF=0x3f3f3f3f; 7 inline int read() 8 { 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 11 while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();} 12 return x*f; 13 } 14 const int M=10005; 15 const int N=1005; 16 const double eps=1e-6; 17 int n,m; 18 double a[M][N],b[M],c[N],v; 19 inline void pivot(int l,int e)//矩阵的转秩 20 { 21 b[l]/=a[l][e]; 22 for(int j=1;j<=n;++j) 23 { 24 if(j!=e) a[l][j]/=a[l][e]; 25 } 26 a[l][e]=1/a[l][e]; 27 for(int i=1;i<=m;++i) 28 { 29 if(i!=l&&fabs(a[i][e])>0) 30 { 31 b[i]-=a[i][e]*b[l]; 32 for(int j=1;j<=n;++j) 33 { 34 if(j!=e) a[i][j]-=a[i][e]*a[l][j]; 35 } 36 a[i][e]=-a[i][e]*a[l][e]; 37 } 38 } 39 v+=c[e]*b[l]; 40 for(int j=1;j<=n;++j) 41 { 42 if(j!=e) c[j]-=c[e]*a[l][j]; 43 } 44 c[e]=-c[e]*a[l][e]; 45 } 46 47 inline double simplex() 48 { 49 while(1) 50 { 51 int e=0,l=0; 52 for(e=1;e<=n;++e) 53 { 54 if(c[e]>eps) break; 55 } 56 if(e==n+1) return v; 57 double mn=INF; 58 for(int i=1;i<=m;++i) 59 { 60 if(a[i][e]>eps&&mn>b[i]/a[i][e]) mn=b[i]/a[i][e],l=i; 61 } 62 if(mn==INF) return INF; 63 pivot(l,e); 64 } 65 } 66 67 int main() 68 { 69 n=read(),m=read(); 70 for(int i=1;i<=n;++i) c[i]=read(); 71 for(int i=1;i<=m;++i) 72 { 73 int s,t; 74 s=read(),t=read(); 75 for(int j=s;j<=t;++j) a[i][j]=1; 76 b[i]=read(); 77 } 78 printf("%d ",(int)(simplex()+0.5)); 79 return 0; 80 }
