处理回文串,Manacher算法也是很不错,但在有些问题的处理上比较麻烦,比如求本质不同的子串的数量还需要结合后缀数组才能解决。今天的们介绍一种能够方便的解决关于回文串的问题的算法--PAM.
一些功能:
假设我们有一个串S,S下标从0开始:
1.求串S前缀0~i内本质不同回文串的个数(两个串长度不同或者长度相同且至少有一个字符不同便是本质不同)
2.求串S内每一个本质不同回文串出现的次数
3.求串S内回文串的个数(其实就是1和2结合起来)
4.求以下标i结尾的回文串的个数
构建回文数树
那么我们该如何构造回文树?
首先我们定义一些变量。
1.len[i] 表示编号为i的节点表示的回文串的长度(一个节点表示一个回文串)
2.next[i][c] 表示编号为i的节点表示的回文串在两边添加字符c以后变成的回文串的编号(和字典树类似)。
3.fail[i] 表示节点i失配以后跳转不等于自身的节点i表示的回文串的最长后缀回文串(和AC自动机类似)。
4.cnt[i] 表示i表示的回文字符串在整个字符串中出现了多少次(建树时求出的不是完全的,最后count()函数跑一遍以后才是正确的)
5.num[i] 表示以节点i表示的最长回文串的最右端点为回文串结尾的回文串个数。
6.last 指向新添加一个字母后所形成的最长回文串表示的节点。
7.S[i] 表示第i次添加的字符(一开始设S[0] = -1(可以是任意一个在串S中不会出现的字符))。
8.p 表示添加的节点个数。
9.n 表示添加的字符个数。
一开始回文树有两个节点,0表示偶数长度串的根和1表示奇数长度串的根,且len[0] = 0,len[1] = -1,last = 0,S[0] = -1,n = 0,p = 2(添加了节点0、1)。

假设现在我们有串S = abbaabba。
首先我们添加第一个字符'a',S[++ n] = 'a',然后判断此时S[n - len[last] - 1]是否等于S[n],即上一个串-1的位置和新添加的位置是否相同,相同则说明构成回文。否则,last = fail[last]。此时last = 0,我们发现S[1 - 0 - 1] != S[1],所以last = fail[last] = 1,然后我们发现S[1 - (-1) - 1] == S[1](即自己等于自己,所以我们让len[1]等于-1可以让这一步更加方便)。
令cur等于此时的last(即cur = last = 1),判断此时next[cur]['a']是否已经有后继,如果next[cur]['a']没有后继,我们就进行如下的步骤:新建节点(节点数p++,且之后p = 3),并让now等于新节点的编号(now = 2),则len[now] = len[cur] + 2(每一个回文串的长度总是在其最长子回文串的基础上在两边加上两个相同的字符构成的,所以是+2,同时体现出我们让len[1] = -1的优势,一个字符自成一个奇回文串时回文串的长度为(-1) + 2 = 1)。然后我们让fail[now] = next[get_fail ( fail[cur] )]['a'],即得到fail[now](此时为fail[2] = 0),其中的get_fail函数就是让找到第一个使得S[n - len[last] - 1] == S[n]的last。然后next[cur]['a'] = now。
当上面步骤完成后我们让last = next[cur][c](不管next[cur]['a']是否有后继),然后cnt[last] ++。
此时回文树为下图状态: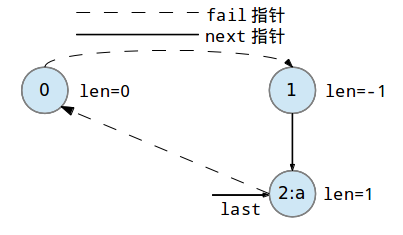

现在我们添加第二个字符字符'b'到回文树中:
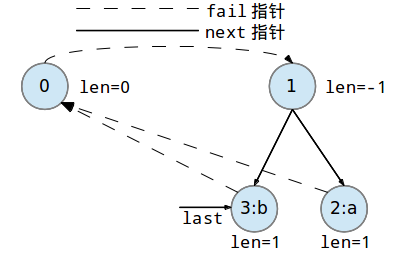
继续添加第三个字符'b'到回文树中:

继续添加第四个字符'a'到回文树中:
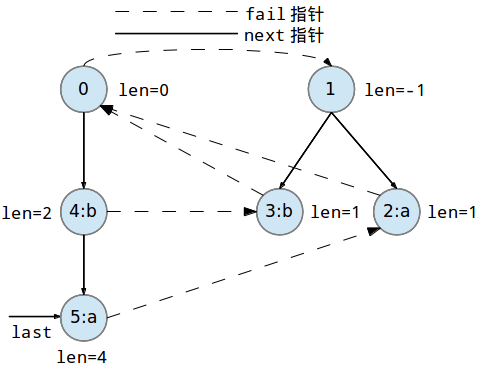
继续添加第五个字符'a'到回文树中:

继续添加第六个字符'b'到回文树中:
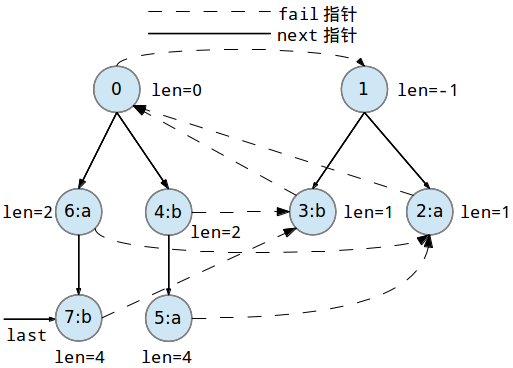
继续添加第七个字符'b'到回文树中:

继续添加第八个字符'a'到回文树中:
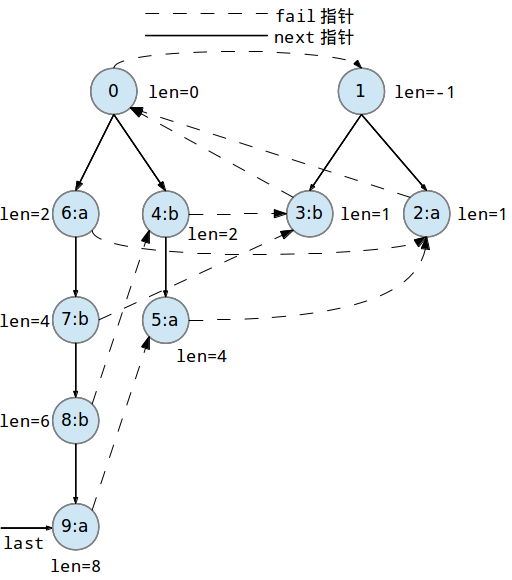

到此,串S已经完全插入到回文树中了,现在所有的数据如下:
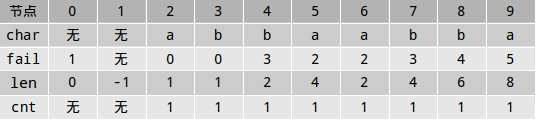
然后我们将节点x在fail指针树中将自己的cnt累加给父亲,从叶子开始倒着加,最后就能得到串S中出现的每一个本质不同回文串的个数。
构造回文树需要的空间复杂度为O(N*字符集大小),时间复杂度为O(N*log(字符集大小)),这个时间复杂度比较神奇。如果空间需求太大,可以改成邻接表的形式存储,不过相应的要牺牲一些时间。
参考模版

1 struct Palindromic_Tree{ 2 int next[MAXN][26]; 3 int fail[MAXN]; 4 int cnt[MAXN]; 5 int num[MAXN]; 6 int len[MAXN]; 7 int S[MAXN]; 8 int last; 9 int n; 10 int p; 11 12 int newnode(int l) 13 { 14 for(int i=0;i<26;++i) next[p][i]=0; 15 cnt[p]=0; 16 num[p]=0; 17 len[p]=l; 18 return p++; 19 } 20 21 void Init() 22 { 23 p=0; 24 newnode( 0); 25 newnode(-1); 26 last=0; 27 n=0; 28 S[n]=-1; 29 fail[0]=1; 30 } 31 32 int get_fail(int x) 33 { 34 while(S[n-len[x]-1]!=S[n])x=fail[x] ; 35 return x ; 36 } 37 38 void add(int c) 39 { 40 S[++ n]=c; 41 int cur=get_fail(last) ; 42 if(!next[cur][c]) 43 { 44 int now=newnode(len[cur]+2) ; 45 fail[now]=next[get_fail(fail[cur])][c] ; 46 next[cur][c]=now ; 47 num[now]=num[fail[now]]+1; 48 } 49 last=next[cur][c]; 50 cnt[last]++; 51 } 52 53 ll count() 54 { 55 ll res=p*1ll; 56 for(int i=p-1;i>=0;--i) cnt[fail[i]]+=cnt[i]; 57 return (res-2);//本质不同的回文串数量 58 } 59 } pam;
