一:N条直线分割平面
假设,x条线能将平面分为f(x)份,这对于份f(n) 第n条线,和其他n-1条线都有交点时,增加量最大,为n;
则: f(n)=f(n-1)+n;
有f(0)=1;得到:n 条直线分割平面的数量最大为:f(n)=n*(n+1)/2 + 1;
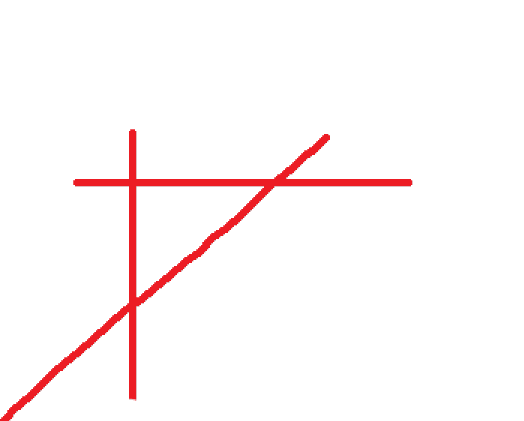
二. “V” 形线分割平面
对于“V”,我们可以把他们当成两条相交直线去掉两条射线。如下图:

上图为两条‘V’形线,对于每条‘V’形线,都相当于两条直线去掉后面两天射线,二去掉这两条射线会使平面减少2,
一因此,有直线公式转化得到: F(n)=f(2n)-2n=2n(2n+1)/2+1-2n;
三. 'N'形线
‘N’形线份两种,一种是有两条平行边,二是没有平行边;
对于没有平行边的情况吧,推导过程和‘V’形线相似,

我们可以将其看成3条直线相交,然后去掉4条射线,去掉这4条射线后,会使平面相对于3条直线减少6;
有直线公式颗推得:
f(N)=f(3n)-6n=3n(3n+1)/2+1-6n;
如果是有平行,得情况则相对于没有的情况减少一个平面;
即为: f(N)=f(3n)=3n(3n+1)/2 + 1 - 5n;