Just A Mistake
Time Limit: 5000/5000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 168 Accepted Submission(s): 41
Problem Description
As we all know, Matt is an outstanding contestant in ACM-ICPC. Graph problems are his favorite.
Once, he came up with a simple algorithm for finding the maximal independent set in trees by mistake.
A tree is a connected undirected graph without cycles, and an independent set is subset of the vertex set which contains no adjacent vertex pairs.
Suppose that the tree contains N vertices, conveniently numbered by 1,2, . . . , N. First, Matt picks a permutation p1, p2, . . . , pN of {1, 2, 3, . . . , N } randomly and uniformly.
After picking the permutation, Matt does the following procedure.
1.Set S =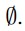 .
.
2.Consider the vertex p1, p2, . . . , pN accordingly. For vertex pi, if and only if there is no vertex in S which is adjacent to pi, add vertex pi into S.
3.Output the set S.
Clearly the above algorithm does not always output the maximal independent set. Matt would like to know the expected size of set S instead.
Once, he came up with a simple algorithm for finding the maximal independent set in trees by mistake.
A tree is a connected undirected graph without cycles, and an independent set is subset of the vertex set which contains no adjacent vertex pairs.
Suppose that the tree contains N vertices, conveniently numbered by 1,2, . . . , N. First, Matt picks a permutation p1, p2, . . . , pN of {1, 2, 3, . . . , N } randomly and uniformly.
After picking the permutation, Matt does the following procedure.
1.Set S =
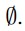 .
.2.Consider the vertex p1, p2, . . . , pN accordingly. For vertex pi, if and only if there is no vertex in S which is adjacent to pi, add vertex pi into S.
3.Output the set S.
Clearly the above algorithm does not always output the maximal independent set. Matt would like to know the expected size of set S instead.
Input
The first line contains only one integer T , which indicates the number of test cases.
For each test case, the first line contains an integer N (1 ≤ N ≤ 200), indicating the number of vertices in the graph.
Each of the following N - 1 lines contains two integers u, v (1 ≤ u, v ≤ N ) indicating an edge between u and v. You may assume that all the vertices are connected.
For each test case, the first line contains an integer N (1 ≤ N ≤ 200), indicating the number of vertices in the graph.
Each of the following N - 1 lines contains two integers u, v (1 ≤ u, v ≤ N ) indicating an edge between u and v. You may assume that all the vertices are connected.
Output
For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the answer. To avoid rounding error, the answer you should output is:
(the expected size of independent set) × N! mod (109 + 7)
Sample Input
2
4
1 2
1 3
1 4
3
1 2
2 3
Sample Output
Case #1: 60
Case #2: 10
Hint
In the first sample, there are 4 vertices, so there are 4! permutations Matt may get.
Suppose the permutation Matt gets is 1 2 3 4. He will add vertex 1 into the independent set.
Suppose the permutation Matt gets is 2 1 3 4. He will add vertex 2, vertex 3 and vertex 4 into the independent set.
It is obvious that if the first element in the permutation is not vertex 1, he will get an independent set whose size is 3. Otherwise, he well get an independent set whose size is 1. Since there are 18
permutations whose first element is not vertex 1, the answer in the first sample is (3 × 18 + 1 × 6) mod (10^9 + 7) = 60.
Source
Recommend
liuyiding
签到题:
参考代码:

1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e6 + 5; 4 int a[maxn]; 5 6 int main() 7 { 8 int t; 9 scanf("%d", &t); 10 for(int k = 1; k <= t; k++) 11 { 12 int n; 13 scanf("%d", &n); 14 for(int i = 1; i <= n; i++) 15 scanf("%d", &a[i]); 16 int min_a = a[n], ans = 0; 17 for(int i = n - 1; i > 0; i--) 18 { 19 if(a[i] > min_a) ans++; 20 else min_a = a[i]; 21 } 22 printf("Case #%d: %d ", k, ans); 23 } 24 return 0; 25 }
