转载:http://blog.csdn.net/hguisu/article/details/8013489
HITS算法是链接分析中非常基础且重要的算法,目前已被Teoma搜索引擎(www.teoma.com)作为链接分析算法在实际中使用。
Hub页面(枢纽页面)和Authority页面(权威页面)是HITS算法最基本的两个定义。
所谓“Authority”页面,是指与某个领域或者某个话题相关的高质量网页,比如搜索引擎领域,Google和百度首页即该领域的高质量网页,比如视频领域,优酷和土豆首页即该领域的高质量网页。
所谓“Hub”页面,指的是包含了很多指向高质量“Authority”页面链接的网页,比如hao123首页可以认为是一个典型的高质量“Hub”网页。
图1给出了一个“Hub”页面实例,这个网页是斯坦福大学计算语言学研究组维护的页面,这个网页收集了与统计自然语言处理相关的高质量资源,包括一些著名的开源软件包及语料库等,并通过链接的方式指向这些资源页面。这个页面可以认为是“自然语言处理”这个领域的“Hub”页面,相应的,被这个页面指向的资源页面,大部分是高质量的“Authority”页面。
HITS算法的目的即是通过一定的技术手段,在海量网页中找到与用户查询主题相关的高质量“Authority”页面和“Hub”页面,尤其是“Authority”页面,因为这些页面代表了能够满足用户查询的高质量内容,搜索引擎以此作为搜索结果返回给用户
基本假设1:一个好的“Authority”页面会被很多好的“Hub”页面指向;
基本假设2:一个好的“Hub”页面会指向很多好的“Authority”页面;
具体算法:可利用上面提到的两个基本假设,以及相互增强关系等原则进行多轮迭代计算,每轮迭代计算更新每个页面的两个权值,直到权值稳定不再发生明显的变化为止。
步骤:
3.1 根集合
1)将查询q提交给基于关键字查询的检索系统,从返回结果页面的集合总取前n个网页(如n=200),作为根集合(root set),记为root,则root满足:
1).root中的网页数量较少
2).root中的网页是与查询q相关的网页
3).root中的网页包含较多的权威(Authority)网页
这个集合是个有向图结构:![]()
3.2 扩展集合base
在根集root的基础上,HITS算法对网页集合进行扩充(参考图2)集合base,扩充原则是:凡是与根集内网页有直接链接指向关系的网页都被扩充到集合base,无论是有链接指向根集内页面也好,或者是根集页面有链接指向的页面也好,都被扩充进入扩展网页集合base。HITS算法在这个扩充网页集合内寻找好的“Hub”页面与好的“Authority”页面。

3.3 计算扩展集base中所有页面的Hub值(枢纽度)和Authority值(权威度)
1)  、
、 分别表示网页结点 i 的Authority值(权威度)和Hub值(中心度)。
分别表示网页结点 i 的Authority值(权威度)和Hub值(中心度)。
2) 对于“扩展集base”来说,我们并不知道哪些页面是好的“Hub”或者好的“Authority”页面,每个网页都有潜在的可能,所以对于每个页面都设立两个权值,分别来记载这个页面是好的Hub或者Authority页面的可能性。在初始情况下,在没有更多可利用信息前,每个页面的这两个权值都是相同的,可以都设置为1,即:

3)每次迭代计算Hub权值和Authority权值:
网页 a (i)在此轮迭代中的Authority权值即为所有指向网页 a (i)页面的Hub权值之和:
a (i) = Σ h (i) ;
网页 a (i)的Hub分值即为所指向的页面的Authority权值之和:
h (i) = Σ a (i) 。
对a (i)、h (i)进行规范化处理:
将所有网页的中心度都除以最高中心度以将其标准化:
a (i) = a (i)/|a(i)| ;
将所有网页的权威度都除以最高权威度以将其标准化:
h (i) = h (i)/ |h(i)| :
5)如此不断的重复第4):上一轮迭代计算中的权值和本轮迭代之后权值的差异,如果发现总体来说权值没有明显变化,说明系统已进入稳定状态,则可以结束计算,即a ( u),h(v)收敛 。
算法描述:

如图3所示,给出了迭代计算过程中,某个页面的Hub权值和Authority权值的更新方式。假设以A(i)代表网页i的Authority权值,以H(i)代表网页i的Hub权值。在图6-14的例子中,“扩充网页集合”有3个网页有链接指向页面1,同时页面1有3个链接指向其它页面。那么,网页1在此轮迭代中的Authority权值即为所有指向网页1页面的Hub权值之和;类似的,网页1的Hub分值即为所指向的页面的Authority权值之和。
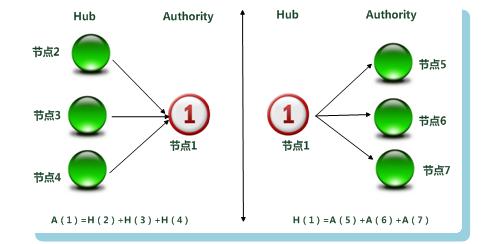
图3 Hub与Authority权值计算
3.4 输出排序结果
将页面根据Authority权值得分由高到低排序,取权值最高的若干页面作为响应用户查询的搜索结果输出。
4. HITS算法存在的问题
HITS算法整体而言是个效果很好的算法,目前不仅应用在搜索引擎领域,而且被“自然语言处理”以及“社交分析”等很多其它计算机领域借鉴使用,并取得了很好的应用效果。尽管如此,最初版本的HITS算法仍然存在一些问题,而后续很多基于HITS算法的链接分析方法,也是立足于改进HITS算法存在的这些问题而提出的。
归纳起来,HITS算法主要在以下几个方面存在不足:
1.计算效率较低
因为HITS算法是与查询相关的算法,所以必须在接收到用户查询后实时进行计算,而HITS算法本身需要进行很多轮迭代计算才能获得最终结果,这导致其计算效率较低,这是实际应用时必须慎重考虑的问题。
2.主题漂移问题
如果在扩展网页集合里包含部分与查询主题无关的页面,而且这些页面之间有较多的相互链接指向,那么使用HITS算法很可能会给予这些无关网页很高的排名,导致搜索结果发生主题漂移,这种现象被称为“紧密链接社区现象”(Tightly-Knit CommunityEffect)。
3.易被作弊者操纵结果
HITS从机制上很容易被作弊者操纵,比如作弊者可以建立一个网页,页面内容增加很多指向高质量网页或者著名网站的网址,这就是一个很好的Hub页面,之后作弊者再将这个网页链接指向作弊网页,于是可以提升作弊网页的Authority得分。
4.结构不稳定
所谓结构不稳定,就是说在原有的“扩充网页集合”内,如果添加删除个别网页或者改变少数链接关系,则HITS算法的排名结果就会有非常大的改变。
5. HITS算法与PageRank算法比较
HITS算法和PageRank算法可以说是搜索引擎链接分析的两个最基础且最重要的算法。从以上对两个算法的介绍可以看出,两者无论是在基本概念模型还是计算思路以及技术实现细节都有很大的不同,下面对两者之间的差异进行逐一说明。
1.HITS算法是与用户输入的查询请求密切相关的,而PageRank与查询请求无关。所以,HITS算法可以单独作为相似性计算评价标准,而PageRank必须结合内容相似性计算才可以用来对网页相关性进行评价;
2.HITS算法因为与用户查询密切相关,所以必须在接收到用户查询后实时进行计算,计算效率较低;而PageRank则可以在爬虫抓取完成后离线计算,在线直接使用计算结果,计算效率较高;
3.HITS算法的计算对象数量较少,只需计算扩展集合内网页之间的链接关系;而PageRank是全局性算法,对所有互联网页面节点进行处理;
4.从两者的计算效率和处理对象集合大小来比较,PageRank更适合部署在服务器端,而HITS算法更适合部署在客户端;
5.HITS算法存在主题泛化问题,所以更适合处理具体化的用户查询;而PageRank在处理宽泛的用户查询时更有优势;
6.HITS算法在计算时,对于每个页面需要计算两个分值,而PageRank只需计算一个分值即可;在搜索引擎领域,更重视HITS算法计算出的Authority权值,但是在很多应用HITS算法的其它领域,Hub分值也有很重要的作用;
7.从链接反作弊的角度来说,PageRank从机制上优于HITS算法,而HITS算法更易遭受链接作弊的影响。
8.HITS算法结构不稳定,当对“扩充网页集合”内链接关系作出很小改变,则对最终排名有很大影响;而PageRank相对HITS而言表现稳定,其根本原因在于PageRank计算时的“远程跳转”
package com.bupt.acm; import java.util.Scanner; /** * Hits算法 HITS算法的目的即是通过一定的技术手段,在海量网页中找到与用户查询主题相关的高质量“Authority”页面和“Hub”页面,尤其是“ * Authority”页面,因为这些页面代表了能够满足用户查询的高质量内容,搜索引擎以此作为搜索结果返回给用户 * * @author DELL * */ public class Hits { public static void main(String[] args){ Scanner scanner=new Scanner(System.in); double[][] authority; double[][] hub; int[][] vertexs; int m,K; System.out.println("开始。。。"); while(scanner.hasNext()){ m=scanner.nextInt();//表示节点的个数 if(m<=0){ System.out.println("输入不合法默认m="+10); m=10; } System.out.println("输入迭代次数k"); K=scanner.nextInt();//表示计算迭代次数 //构造输入矩阵,0:表示不链接;1:表示链接 vertexs=new int[m][m]; for(int i=0;i<m;i++){ for(int j=0;j<m;j++){ vertexs[i][j]=scanner.nextInt(); } } System.out.println(); authority=new double[K+1][m]; hub=new double[K+1][m]; //该算法首先将所有的中心值和权威值初始化为1 for(int i=0;i<m;i++){ authority[0][i]=1; hub[0][i]=1; } //然后根据刚才介绍的方差更新中心值和权威值 for(int i=1;i<=K;i++){ for(int j=0;j<m;j++){ authority[i][j]=0; hub[i][j]=0; }//0 1 1 1 0 0 1 0 0 1 0 0 1 0 1 0 double za=0,zh=0; for(int j=0;j<m;j++){ for(int k=0;k<m;k++){ if(vertexs[j][k]!=0){ hub[i][j]+=authority[i-1][k]; System.out.println("hub["+i+"]["+j+"]="+hub[i][j]); zh=zh+authority[i-1][k]; System.out.println("zh="+zh); } if(vertexs[k][j]!=0){ authority[i][j]+=hub[i-1][k]; System.out.println("authority["+i+"]["+j+"]="+authority[i][j]); za+=hub[i-1][k]; System.out.println("za="+za); } } } //对任意节点,计算authority和hub值 System.out.println("za:"+za+"; zh:"+zh); for(int j=0;j<m;j++){ authority[i][j]/=za; hub[i][j]/=zh; } } System.out.println("输出结果:"); for(int i=0;i<=K;i++){ for(int j=0;j<m;j++){ System.out.print(" authority:"+authority[i][j]+" hub"+hub[i][j]); } System.out.println(" ---------------------------------"); } } } }