1.简介
树状数组是一种初级数据结构,凡是他能做的事情,都可以交给线段树来完成,但是树状数组的书写十分容易,所以很多情况我们都用树状数组来写。
Q:我们为什么要引入树状数组的概念?
A:因为查询区间和,如果用数组的话,那么查询的时候是O(N),修改可以是O(1)。用前缀和查询是O(1),但是修改是O(N)
因此我们提出了一种查询和修改都不是特别慢,也不是特别快的想法,这样可以降低时间复杂度,所以我们提出了树状数组的概念
2.原理
树状数组借鉴了二进制划分范围的思想,下面我们由二进制的想法来引出树状数组。
对于一个数X,他可以被表示为X=2^vk+2^vk-1+……+2^v1
因此他可以被分割成一个个区间:
(X-2^v1,X]
(X-2^v2-2^v1,x-2^v1]
……
(0,x-2^vk-2^vk1-……2^v1]
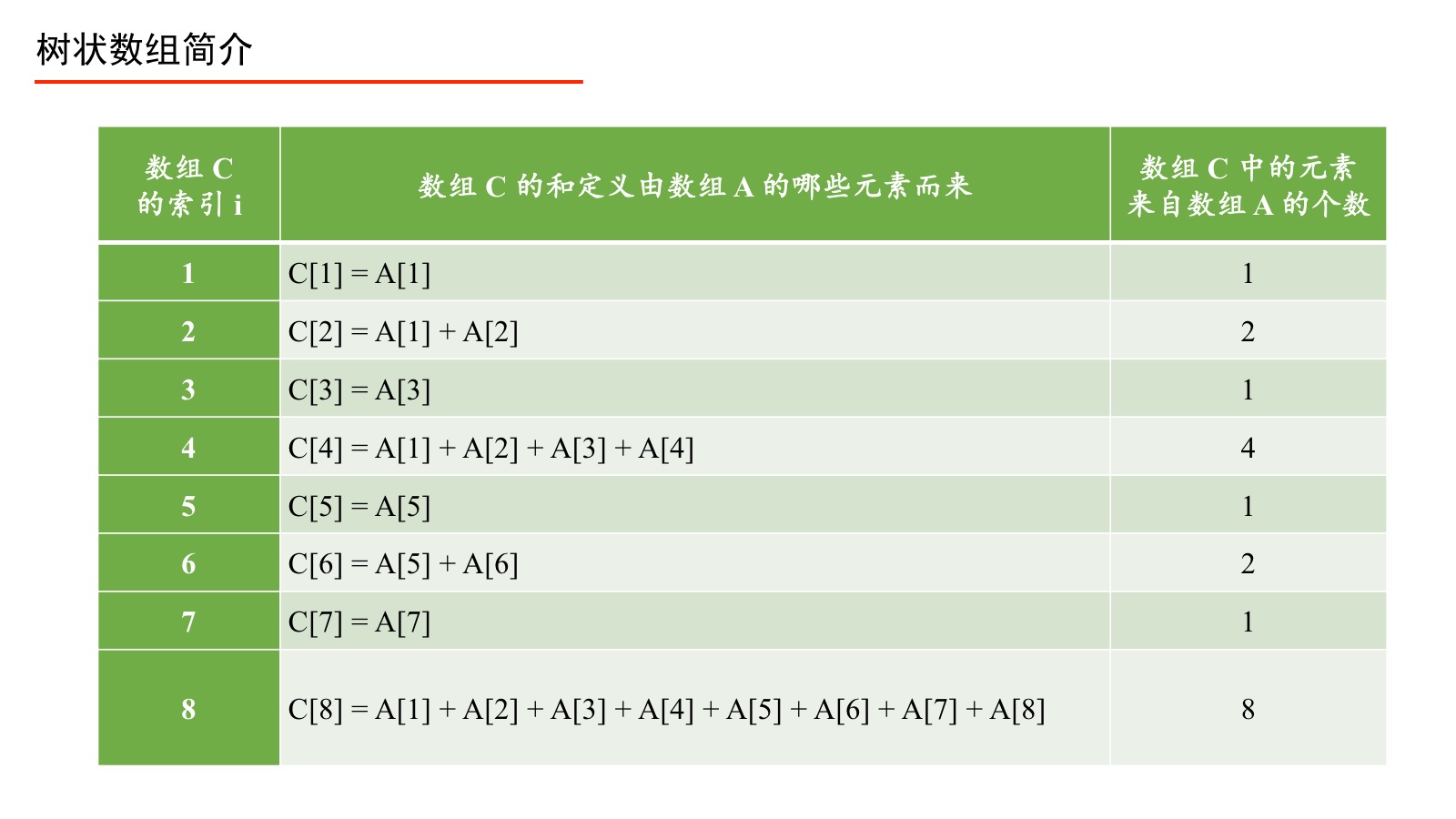
从这个思路引出树状数组的想法,我们定义C[X]=A(x-2^k+1,X),其中A代表原数组,C代表部分区间和。C[X]的长度是lowbit(x),也就是最后一个1所在的位置。
我们需要快速的求出原数组的指定前缀和,我们可以把前缀和划分成很多个C[X],这样就能在log范围内求出前缀和了,那么如何知道C[X]代表什么呢?
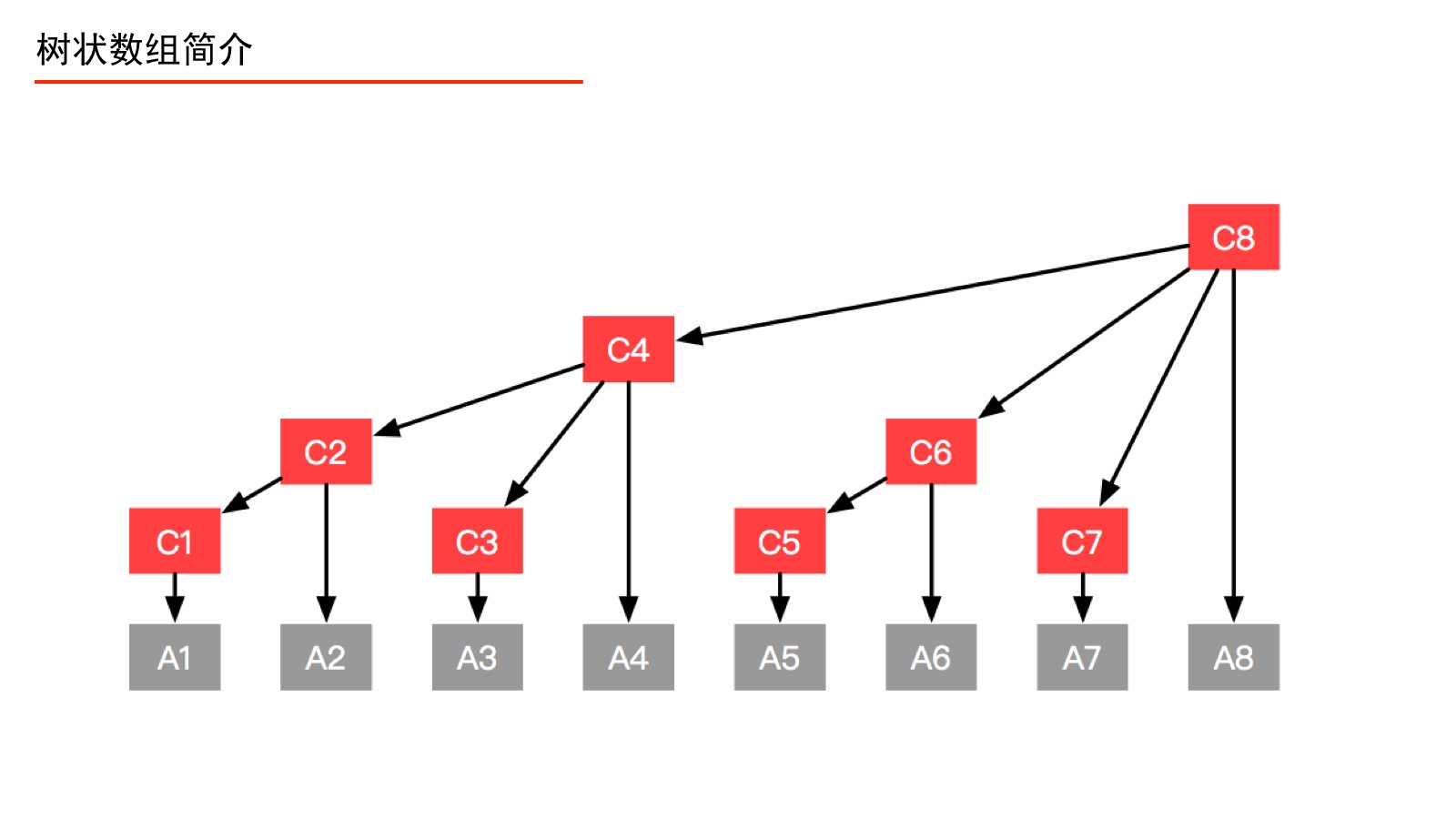
对于每一个C[X],他的长度都是lowbit(X),根据图形,我们可以把他看作是树的形式,那么如何知道父节点子节点的关系呢?
我们以C8为例来讲解:
8的二进制形式为1000,所以他的长度为8,我们要将他表示为几个C相加的关系,根据上面二进制的思路,每个X都是可以被划分成多个区间,那么C8可以被划分成A8+A(x-2^k+1,x-1)
剩下的X-1可以表示成很多形如01……10这样的前面有连续1后面是连续0的区间,这些区间就是他的子节点。比如C8的子节点就包括C7,C6,C4,因为1000-1=0111,包含(0110,0111),(0100,0110),(0000,0100),其实就是不断对x-1求lowbit直到0,注意不是对原数一直到0,比如1100,最终求到的是1000而不是0000,也就是对最末尾的1之后的数求lowbit。
这样就找打子节点和父节点的关系,根据这个关系我们可以看出,每个子节点的父亲都唯一确定,这也是树的特征,因此对原数组进行更新,只要不断地对父节点进行更新直到最大即可,这样保证了树状数组求前缀和的合理性。
3.用法
树状数组普遍适用于以下情况:
1.对一段区间+数
2.查询区间和
3.对一段区间+数后查询原数组中的数据
4.对一段区间+数后查询区间和
总结,只要看出要是对区间加减和求区间和就能用树状数组来写,很多问题可以转化成这两个问题
下面提供数组更新和查询的函数即树状数组常用函数:

int lowbit(int x){ //lowbit函数 return x&-x; } void add(int x,int c){ //单点修改函数 int i; for(i=x;i<=n;i+=lowbit(i)){ tr[i]+=c; } } int sum(int x){//区间查询函数 int res=0; int i; for(i=x;i;i-=lowbit(i)){ res+=tr[i]; } return res; }
4.例题
一、
给定长度为N的数列A,然后输入M行操作指令。
第一类指令形如“C l r d”,表示把数列中第l~r个数都加d。
第二类指令形如“Q X”,表示询问数列中第x个数的值。
对于每个询问,输出一个整数表示答案。
根据题意显然可以看出这是对区间加数并求原数组,一般可以设计差分数组,对差分数组求和就是原函数
二、
给定一个长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“C l r d”,表示把 A[l],A[l+1],…,A[r] 都加上 d。
2、“Q l r”,表示询问 数列中第 l~r 个数的和。
对于每个询问,输出一个整数表示答案。
根据题意,这是对区间加数并求区间和,这题需要变形,根据题目写出公式,并对公式变形,设计两个树状数组。

#include<iostream> #include<cstring> #include<string> #include<cmath> #include<algorithm> #include<map> #include<vector> #include<cstdio> #include <unordered_map> using namespace std; const int N=1e5+10; const int inf=0x3f3f3f3f; typedef long long ll; int a[N]; ll tr1[N]; ll tr2[N]; ll res1,res2; int n; int lowbit(int x){ return x&-x; } void add(ll tr[],int x,ll c){ int i; for(i=x;i<=n;i+=lowbit(i)){ tr[i]+=c; } } ll sum(ll tr[],int x){ ll res=0; int i; for(i=x;i;i-=lowbit(i)){ res+=tr[i]; } return res; } ll sum1(int x){ return sum(tr1,x)*(x+1)-sum(tr2,x); } int main(){ int m; int i; cin>>n>>m; for(i=1;i<=n;i++) scanf("%d",&a[i]); for(i=1;i<=n;i++){ int b=a[i]-a[i-1]; add(tr1,i,b); add(tr2,i,(ll)b*i); } while(m--){ int d; string s; int l,r; cin>>s>>l; if(s=="C"){ cin>>r>>d; add(tr1,l,(ll)d); add(tr2,l,(ll)d*l); add(tr1,r+1,(ll)-d); add(tr2,r+1,(ll)(-d)*(r+1)); } else{ cin>>r; cout<<sum1(r)-sum1(l-1)<<endl; } } }
三、
有n头奶牛,已知它们的身高为 1~n 且各不相同,但不知道每头奶牛的具体身高。
现在这n头奶牛站成一列,已知第i头牛前面有AiAi头牛比它低,求每头奶牛的身高。
本题显然需要倒序求解,这样我们可以知道对于每个i,他的高度都是剩下来数中的ai+1大,因为用到了区间减以及区间求和,可以用树状数组,再结合二分即可。
4.总结
树状数组原理复杂但是操作简单,使用范围比较单一,需要我们对题目的数据进行发掘,本文中的例题来自《算法竞赛进阶指南》,是我在Acwing网站学习后写下的部分理解,主要是便于自己复习和记录,也希望能够给大家提供帮助,但是由于我的表达能力和对Markdown语法的操作问题,本文对初学者难免会感到晦涩,希望得到大家的理解。在Acwing网站上有一篇十分详细的分享讲述了树状数组,如果有需要可以去食用。
