《统计学习方法》第九章，EM算法

▶ EM 算法的引入，三硬币问题，体验一下不同初始值对收敛点的影响

● 代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle

dataSize = 1000
trainDataRatio = 0.3
defaultTurn = 20
epsilon = 1E-10
randomSeed = 103

def dataSplit(dataY, part):                                     # 将数据集分割为训练集和测试集
    return dataY[:part], dataY[part:]

def createData(realA, realB, realC, count = dataSize):          # 创建数据
    np.random.seed(randomSeed)
    a = (np.random.rand(count) > realA).astype(int)
    b = (np.random.rand(count) > realB).astype(int)
    c = (np.random.rand(count) > realC).astype(int)
    return b * (1 - a) + c * a

def em(dataY, initialA, initialB, initialC, turn = defaultTurn):# 迭代计算
    count = len(dataY)
    sumY = np.sum(dataY)
    a = initialA
    b = initialB
    c = initialC
    for i in range(turn):
        p = a * b ** dataY *(1 - b) ** (1 - dataY) / ( a * b ** dataY *(1 - b) ** (1 - dataY) + (1 - a) * c ** dataY *(1 - c) ** (1 - dataY) )
        sumP = np.sum(p)
        a = sumP / count
        b = np.sum(p * dataY) / sumP
        c = (sumY - np.sum(p * dataY)) / (count - sumP)
    return a, b, c

def test(realA, realB, realC, initialA, initialB, initialC):    # 单次测试
    Y = createData(realA, realB, realC)

    para = em(Y, initialA, initialB, initialC)

    print( "real=(%.3f, %.3f, %.3f),initial=(%.3f,%.3f,%.3f),train=(%.3f,%.3f,%.3f)"%(realA, realB, realC, initialA,initialB,initialC,para[0],para[1],para[2]) )

if __name__ == '__main__':
    test(0.5, 0.5, 0.5, 0.5, 0.5, 0.5)
    test(0.5, 0.5, 0.5, epsilon, epsilon, epsilon)
    test(0.5, 0.5, 0.5, 0.5, epsilon, epsilon)
    test(0.5, 0.5, 0.5, epsilon, 0.5, epsilon)
    test(0.5, 0.5, 0.5, epsilon, epsilon, 0.5)
    test(0.5, 0.5, 0.5, 1.0 - epsilon, epsilon, epsilon)
    test(0.5, 0.5, 0.5, epsilon, 1.0 - epsilon, epsilon)
    test(0.5, 0.5, 0.5, epsilon, epsilon, 1.0 - epsilon)
    test(0.5, 0.5, 0.5, 1.0 - epsilon, 1.0 - epsilon, 1.0 - epsilon)

    test(0.4, 0.5, 0.6, 0.4, 0.5, 0.6)
    test(0.4, 0.5, 0.6, epsilon, epsilon, epsilon)
    test(0.5, 0.5, 0.5, 0.5, epsilon, epsilon)
    test(0.5, 0.5, 0.5, epsilon, 0.5, epsilon)
    test(0.5, 0.5, 0.5, epsilon, epsilon, 0.5)

● 输出结果，从不同的真实值和初始值得到不同的收敛点

real=(0.500, 0.500, 0.500),initial=(0.500,0.500,0.500),train=(0.500,0.516,0.516)
real=(0.500, 0.500, 0.500),initial=(0.000,0.000,0.000),train=(0.000,0.516,0.516)
real=(0.500, 0.500, 0.500),initial=(0.500,0.000,0.000),train=(0.500,0.516,0.516)
real=(0.500, 0.500, 0.500),initial=(0.000,0.500,0.000),train=(0.172,1.000,0.415)
real=(0.500, 0.500, 0.500),initial=(0.000,0.000,0.500),train=(0.000,0.000,0.516)
real=(0.500, 0.500, 0.500),initial=(1.000,0.000,0.000),train=(1.000,0.516,0.516)
real=(0.500, 0.500, 0.500),initial=(0.000,1.000,0.000),train=(0.258,1.000,0.348)
real=(0.500, 0.500, 0.500),initial=(0.000,0.000,1.000),train=(0.242,0.000,0.681)
real=(0.500, 0.500, 0.500),initial=(1.000,1.000,1.000),train=(1.000,0.516,0.516)
real=(0.400, 0.500, 0.600),initial=(0.400,0.500,0.600),train=(0.409,0.406,0.506)
real=(0.400, 0.500, 0.600),initial=(0.000,0.000,0.000),train=(0.000,0.465,0.465)
real=(0.500, 0.500, 0.500),initial=(0.500,0.000,0.000),train=(0.500,0.516,0.516)
real=(0.500, 0.500, 0.500),initial=(0.000,0.500,0.000),train=(0.172,1.000,0.415)
real=(0.500, 0.500, 0.500),initial=(0.000,0.000,0.500),train=(0.000,0.000,0.516)

● 画图，散点位置表示初始取值，散点颜色 RGB 值表示收敛点取值。各图依次为：（真实值 ( 0.5,0.5,0.5 )，初始间隔 0.1，迭代 20 次），（真实值 ( 0.5,0.5,0.5 )，初始间隔 0.1，迭代 100 次），（真实值 ( 0.5,0.5,0.5 )，初始间隔 0.05，迭代 20 次），（真实值 ( 0.3,0.6,0.8 )，初始间隔 0.1，迭代 20 次）。可见：① 迭代 20 次以后就基本稳定了，更多次数迭代没有明显影响；② 随着初始点的连续移动，收敛点的取值耶连续漂移，没有出现明显断层；③ 图中色彩饱和度较高的散点存在，说明收敛点并不能向真实值点明显靠拢，甚至有可能保持极端取值；④ 真实值点对收敛点在整个空间上的取值有影响（废话）

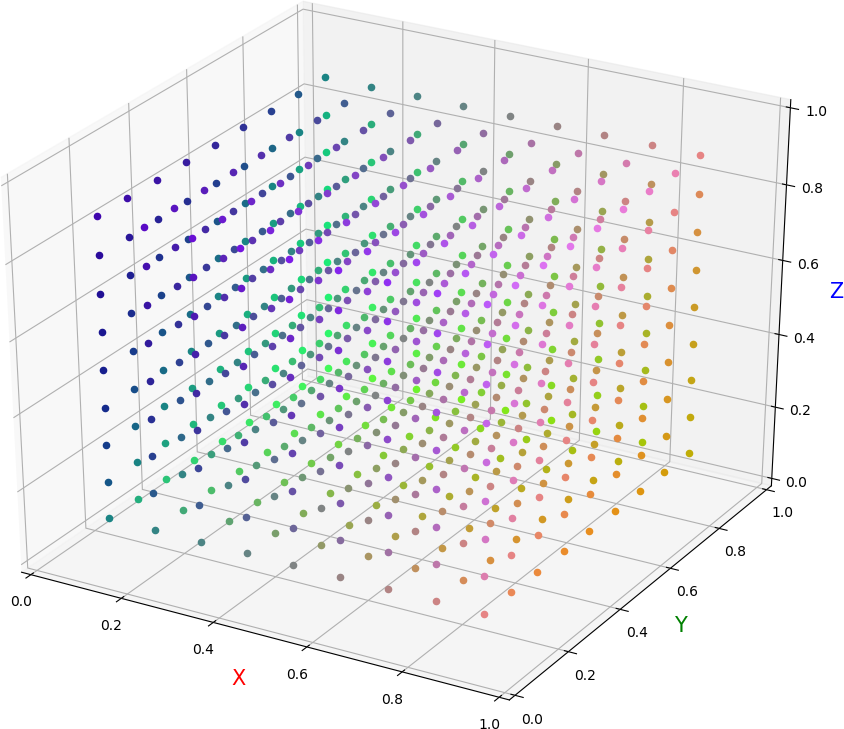
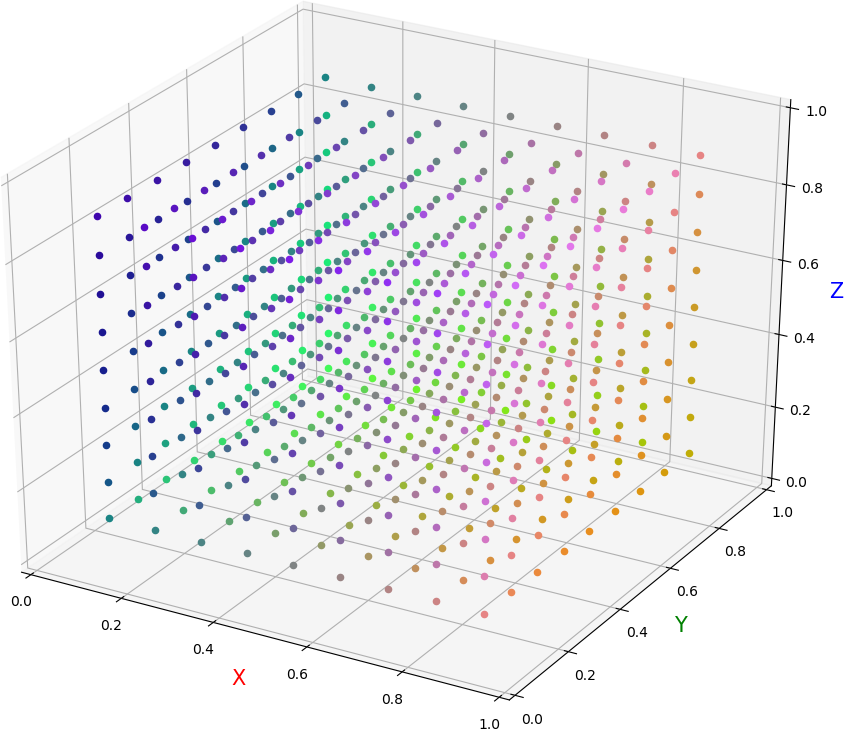
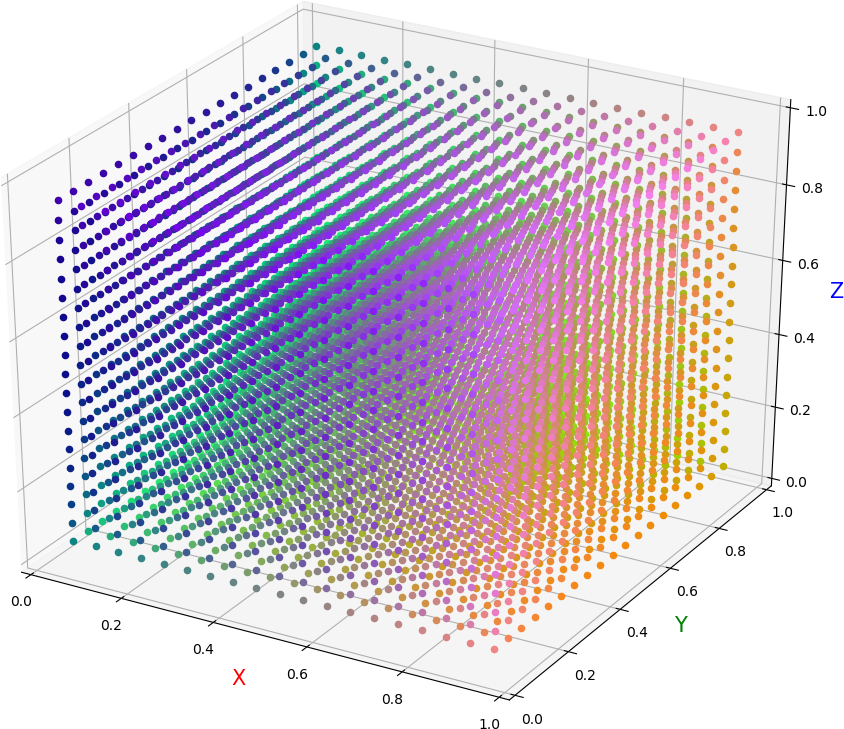
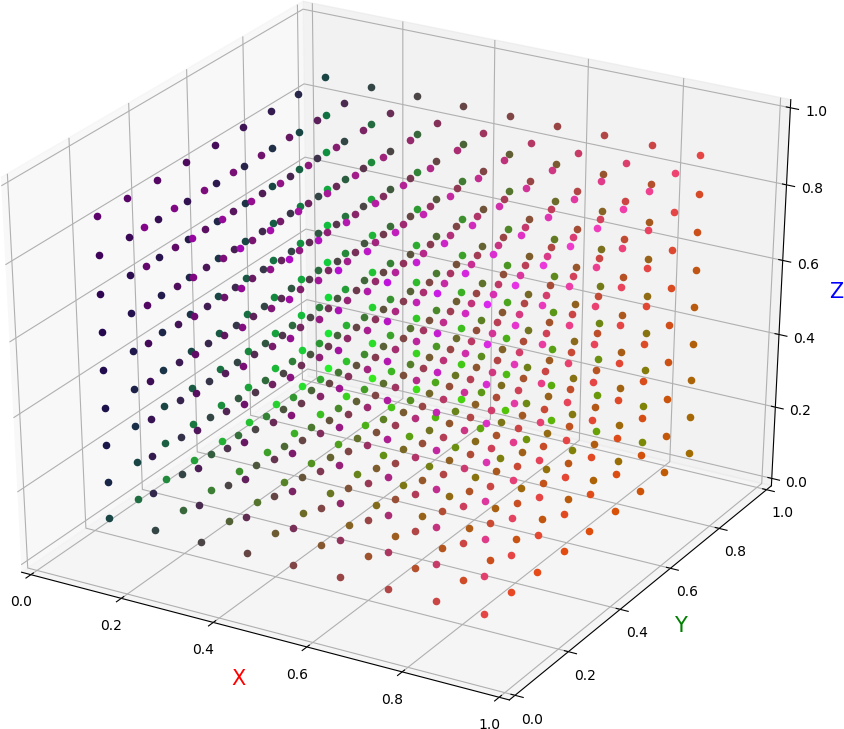
● 画图脚本

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection

dataSize = 1000
trainDataRatio = 0.3
defaultTurn = 20
epsilon = 1E-10
randomSeed = 103

def dataSplit(dataY, part):
    return dataY[:part], dataY[part:]

def myColor(x):
    r = np.select([x < 1/2, x < 3/4, x <= 1, True],[0, 4 * x - 2, 1, 0])
    g = np.select([x < 1/4, x < 3/4, x <= 1, True],[4 * x, 1, 4 - 4 * x, 0])
    b = np.select([x < 1/4, x < 1/2, x <= 1, True],[1, 2 - 4 * x, 0, 0])
    return [r,g,b]

def createData(realA, realB, realC, count = dataSize):
    np.random.seed(randomSeed)
    a = (np.random.rand(count) > realA).astype(int)
    b = (np.random.rand(count) > realB).astype(int)
    c = (np.random.rand(count) > realC).astype(int)
    return b * (1 - a) + c * a

def em(dataY, initialA, initialB, initialC, turn = defaultTurn):
    count = len(dataY)
    sumY = np.sum(dataY)
    a = initialA
    b = initialB
    c = initialC
    for i in range(turn):
        p = a * b ** dataY *(1 - b) ** (1 - dataY) / ( a * b ** dataY *(1 - b) ** (1 - dataY) + (1 - a) * c ** dataY *(1 - c) ** (1 - dataY) )
        sumP = np.sum(p)
        a = sumP / count
        b = np.sum(p * dataY) / sumP
        c = (sumY - np.sum(p * dataY)) / (count - sumP)
    return a, b, c

def test(realA, realB, realC):
    dataY = createData(realA, realB, realC)
    XX, YY, ZZ = np.meshgrid(np.arange(0.1,1.00,0.1), np.arange(0.1,1.00,0.1), np.arange(0.1,1.00,0.1))
    #XX, YY = np.meshgrid(np.arange(0.05,1.00,0.05), np.arange(0.05,1.00,0.05)) # 一个斜截平面
    #ZZ = ( 9 - 5 * XX - 4 * YY ) / 12

    fig = plt.figure(figsize=(10, 8))
    ax = Axes3D(fig)
    ax.set_xlim3d(0.0, 1.0)
    ax.set_ylim3d(0.0, 1.0)
    ax.set_zlim3d(0.0, 1.0)
    ax.set_xlabel('X', fontdict={'size': 15, 'color': 'r'})
    ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'g'})
    ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'b'})

    for xyz in zip(XX.flatten(),YY.flatten(),ZZ.flatten()):
        para = em(dataY, xyz[0], xyz[1], xyz[2])
        para = np.minimum(np.maximum(np.array(para),0),1)
        ax.scatter([xyz[0]], [xyz[1]], [xyz[2]], color = list(para), s = 20, label = "P")
        #ax.scatter([xyz[0]], [xyz[1]], [xyz[2]], color = myColor( np.sum((np.array(para) - np.array([realA,realB,realC]))**2)), s = 20, label = "P")

    fig.savefig("R:\(" + str(round(realA,3)) + "," + str(round(realB,3)) + "," + str(round(realC,3)) + ").png")
    plt.close()

if __name__ == '__main__':
    test(0.5, 0.5, 0.5)

 ● EM 算法用于高斯混合模型，代码

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle

dataSize = 1000
trainDataRatio = 0.3
defaultTurn = 100
epsilon = 1E-5
randomSeed = 103

def dataSplit(dataY, part):                                     # 将数据集分割为训练集和测试集
    return dataY[:part], dataY[part:]

def normalCDF(x, μList, σList):
    return np.exp(-(x - μList)**2 / (2 * σList**2)) / (np.sqrt(2 * np.pi) * σList)
    
def createData(ndistributionCount, count = dataSize):          # 创建数据
    np.random.seed(randomSeed)
    X = np.random.randn(count, ndistributionCount)
    μ = np.cumsum(np.random.rand(ndistributionCount))
    σ = np.random.rand(ndistributionCount)
    α = np.random.rand(ndistributionCount)
    α /= np.sum(α)
    return np.sum(α * (σ * X + μ), 1), μ, σ, α

def em(dataY, ndistributionCount, turn = defaultTurn):      # 迭代计算
    count = len(dataY)    
    Y = np.tile(dataY,[ndistributionCount,1]).T
    μ = np.random.rand(ndistributionCount)
    σ = np.random.rand(ndistributionCount)
    α = np.random.rand(ndistributionCount)
    α /= np.sum(α)

    for i in range(turn):
        p = np.mat(α * normalCDF(Y, μ, σ))
        p = np.array( p / np.sum(p, 1) )
        sumP = np.sum(p, 0)
        μ = np.sum( p * Y ,0) / sumP
        σ = np.sqrt(np.sum( p * (Y - μ)**2 , 0) / sumP)
        α = sumP / count        
    return μ, σ, α

def test(ndistributionCount):    # 单次测试
    dataY, μ, σ, α = createData(ndistributionCount)

    μOut, σOut, αOut = em(dataY, ndistributionCount)

    print("ndistributionCount = " + str(ndistributionCount))
    print("originμ = ", μ)    
    print("train μ = ", μOut)    
    print("originσ = ", σ)    
    print("train σ = ", σOut)    
    print("originα = ", α)  
    print("train α = ", αOut)

if __name__ == '__main__':
    test(1)
    test(2)
    test(3)
    test(4)
    test(5)    

● 输出结果，似乎只有一元的时候收敛，代码有点问题【坑】

ndistributionCount = 1
originμ =  [0.67175814]
train μ =  [0.67842327]
originσ =  [0.14955569]
train σ =  [0.14782499]
originα =  [1.]
train α =  [1.]
ndistributionCount = 2
originμ =  [0.41731305 1.03497633]
train μ =  [0.71810584 0.80326904]
originσ =  [0.8746775  0.54866726]
train σ =  [0.60543201 0.46134878]
originα =  [0.4609127 0.5390873]
train α =  [0.3065564 0.6934436]
ndistributionCount = 3
originμ =  [0.56854648 1.11932014 1.58967158]
train μ =  [1.1911365  1.14824762 1.20370434]
originσ =  [0.20615474 0.13178869 0.09097129]
train σ =  [0.07795558 0.08028857 0.07615437]
originα =  [0.21194169 0.38980503 0.39825329]
train α =  [0.71143915 0.01148389 0.27707696]
ndistributionCount = 4
originμ =  [0.06525055 0.76467489 1.36233954 2.27413522]
train μ =  [0.89375387 1.32709678 1.28927068 0.99696908]
originσ =  [0.04627714 0.05849647 0.88877231 0.57707149]
train σ =  [0.248415   0.26329343 0.25491932 0.12993855]
originα =  [0.0825736  0.39384943 0.2717186  0.25185837]
train α =  [0.08450359 0.41897111 0.44427471 0.05225059]
ndistributionCount = 5
originμ =  [0.55679028 1.13666279 1.88269851 2.33842668 2.65599906]
train μ =  [1.71404135 1.14266766 1.61215492 0.9602133  1.58427791]
originσ =  [0.51241842 0.49056236 0.14953623 0.57604303 0.98916623]
train σ =  [0.22736403 0.14251132 0.26561206 0.02144093 0.2710761 ]
originα =  [0.22618106 0.29204021 0.10173233 0.21445053 0.16559587]
train α =  [0.05202092 0.03445172 0.59535521 0.0073266  0.31084555]