1 引言
1.1 维度灾难
分类为例:如最近邻分类方法(基本思想:以最近的格子投票分类)
问题:当数据维度增大,分类空间爆炸增长。如图1所示,
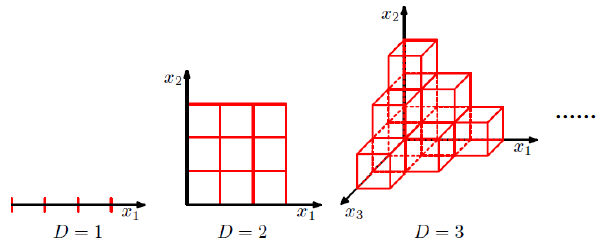
图1 维度增加示意图
1.2 解决方法
缓解维度遭难的一个重用途径是降维。降维是通过某种数学变换,将原始高维属性空间转换为一个低维“子空间”,在这个子空间中样本
密度大幅度提高,距离计算也变得更为容易。
1.3 降维的可行性
数据样本虽然是高维的,但与我们关心的也许仅是某个低维分布,因而可以对数据进行有效的降维。
1.4 主成分分析
1.4.1 概念
主成分分析(Principal Component Analysys,简称PCV),是将具有相关性的高维指标,通过线性变换,化为少数相互独立的低维综合指标的
一种多元统计方法。 又称为主分量分析。使用PCV降维时应该满足:
(1)使降维后样本的方差尽可能大。
(2)使降维后数据的均方误差尽可能小。
1.4.2 基本计算步骤
(1)计算给定样本{xn},n=1,2,...,N的均值mean_x和方差S;
(2)计算S的特征向量与特征值,X = UΛUT;
(3)将特征值从小到大排列,前M个特征值λ1,λ1,...,λM所对应的特征向量u1,u2,...,uM构成投影矩阵。
2 矩阵特征值及特征向量求解
2.1 定义
A为n阶矩阵,若数λ和n维非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量。
式Ax=λx也可写成( A-λE)x=0,并且|λE-A|叫做A 的特征多项式。
|λE-A| = 0,称为A的特征方程(一个齐次线性方程组),求解特征值的过程其实就是求解特征方程的解。
2.2 特征值分解
特征值分解是将一个矩阵分解成下面的形式:

其中Q是这个矩阵A的特征向量组成的矩阵。Σ = diag(λ1, λ2, ..., λn)是一个对角阵,每一个对角线上的元素就是一个特征值。
3 奇异值分解(SVD)
特征值分解只适用于方阵。而在现实的世界中,我们看到的大部分矩阵都不是方阵,我们怎样才能像描述特征值一样描述这样一般矩阵的重要特征呢?奇异值分解(Singular Value Decomposition, 简称SVD)可用来解决这个问题。SVD比特征值分解的使用范围更广,是一个适用于任一矩阵分解的方法。
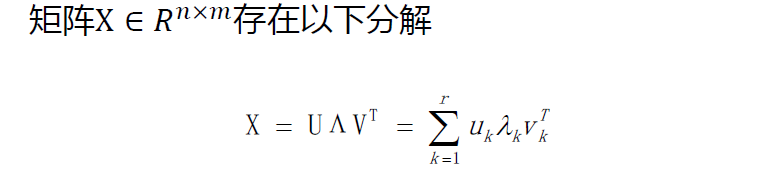
假设X是一个m * n的矩阵,那么得到的U是一个m * m的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),
Σ是一个m * n的实数对角矩阵(对角线以外的元素都是0,对角线上的元素称为奇异值),
VT(V的转置)是一个n * n的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量,
从图片来反映几个相乘的矩阵的大小可得下面的图片,

将一个矩阵X的转置 XT * X,将会得到 XTX 是一个方阵,我们用这个方阵求特征值可以得到:
(ATA)vi = λivi
这里得到的V,就是我们上面的右奇异向量。这里的σi 就是就是上面说的奇异值λi,ui就是上面说的左奇异向量。常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。
奇异值σ跟特征值类似,在矩阵Λ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:

r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子:
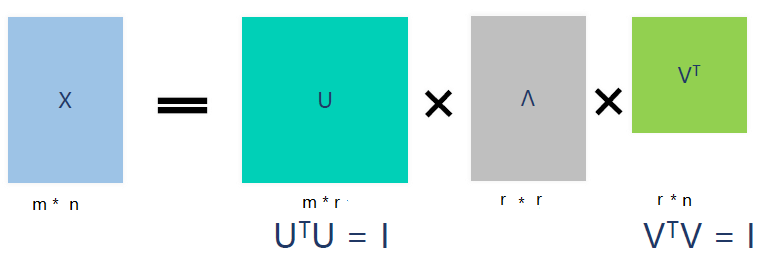
右边的三个矩阵相乘的结果将会是一个接近于X的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Λ、V就好了。
4 特征分解与奇异值分解
4.1 低秩近似(Low-rank Approximation)
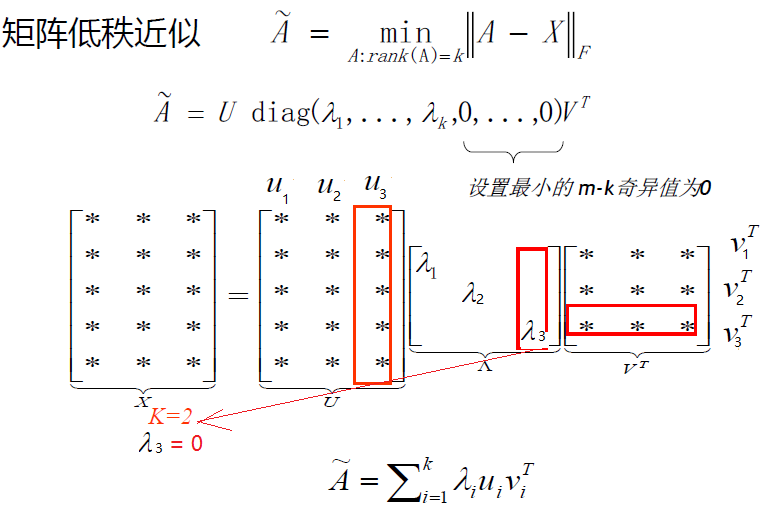
4.2 关联
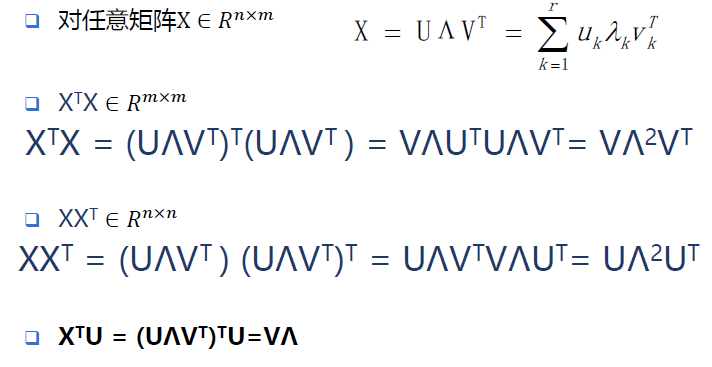
5 pca(matrix)函数代码
1 def pca(X): 2 """ 主成分分析(PCA) 3 输入: X, (每行存储训练数据(一张图像)的扁平数组) 4 返回: 投影矩阵(V,重要维度优先)、方差(S)和均值(mean_X) 5 """ 6 7 # 获得维度:num_data,dim = 图片数量 * 图片大小 ------>图片大小 = 长*宽 8 num_data,dim = X.shape 9 10 # 中心数据 11 mean_X = X.mean(axis=0) # 每列求平均值 得到 1 * dim 12 X = X - mean_X # X.shape = num_data * dim 13 14 if dim > num_data: 15 # PCA - 紧凑的使用技巧 16 M = dot(X,X.T) # 协方差矩阵 17 e,EV = linalg.eigh(M) # e,EV = M的特征值,特征向量 18 tmp = dot(X.T,EV).T # 使用紧凑技巧? 19 V = tmp[::-1] # 为了得到最后的特征向量 20 S = sqrt(e)[::-1] # 反向,因为特征值是递增的 21 for i in range(V.shape[1]): # V.shape[1] = ??? 22 V[:,i] /= S 23 else: 24 # PCA - 使用奇异值分解(SVD) 25 U,S,V = linalg.svd(X) 26 V = V[:num_data] # 只有返回前num_data个才有意义 但是我认为此处不应该为V[:num_data]而应该为 V[:dim] ------>因为num_data >= dim 27 28 # 返回n the projection matrix, the variance and the mean 29 return V,S,mean_X
6 简单实例说明PCV实现的过程
6.1 列数大于行数时
1 # 初始化矩阵X (列数大于行数时) 2 X = [[1 0 1 0 0 0] 3 [0 1 0 0 0 0] 4 [1 1 0 0 0 0] 5 [1 0 0 1 1 0] 6 [0 0 0 1 0 1]] 7 #计算每列的平均值 8 mean_X =X.mean(axis=0)= [0.6 0.4 0.2 0.4 0.2 0.2] 9 # 计算中心数据 10 X =X - mean_X = [[ 0.4 -0.4 0.8 -0.4 -0.2 -0.2] 11 [-0.6 0.6 -0.2 -0.4 -0.2 -0.2] 12 [ 0.4 0.6 -0.2 -0.4 -0.2 -0.2] 13 [ 0.4 -0.4 -0.2 0.6 0.8 -0.2] 14 [-0.6 -0.4 -0.2 0.6 -0.2 0.8]] 15 # 计算协方差矩阵 16 M =dot(X, X.T)=[[ 1.20000000e+00 -4.00000000e-01 5.55111512e-17 -2.00000000e-01 17 -6.00000000e-01] 18 [-4.00000000e-01 1.00000000e+00 4.00000000e-01 -8.00000000e-01 19 -2.00000000e-01] 20 [ 5.55111512e-17 4.00000000e-01 8.00000000e-01 -4.00000000e-01 21 -8.00000000e-01] 22 [-2.00000000e-01 -8.00000000e-01 -4.00000000e-01 1.40000000e+00 23 0.00000000e+00] 24 [-6.00000000e-01 -2.00000000e-01 -8.00000000e-01 0.00000000e+00 25 1.60000000e+00]] 26 # 计算协方差的特征值和特征向量 27 e, EV = numpy.linalg.eigh(M) 28 e = [-6.04093951e-16 2.66097365e-01 1.17478886e+00 2.00000000e+00 29 2.55911378e+00] 30 EV = [[ 4.47213595e-01 -1.38203855e-01 6.92423635e-01 5.00000000e-01 31 -2.26824169e-01] 32 [ 4.47213595e-01 -6.14411448e-01 -1.73966345e-01 -5.00000000e-01 33 -3.77139608e-01] 34 [ 4.47213595e-01 6.98980014e-01 -3.02870626e-01 4.38587603e-16 35 -4.68717745e-01] 36 [ 4.47213595e-01 -2.11286151e-01 -5.40988322e-01 5.00000000e-01 37 4.61183041e-01] 38 [ 4.47213595e-01 2.64921441e-01 3.25401658e-01 -5.00000000e-01 39 6.11498480e-01]] 40 #行之间反转 41 tmp = dot(X.T, EV).T =[[-3.33066907e-16 -3.33066907e-16 4.16333634e-16 -3.33066907e-16 42 -3.88578059e-16 1.66533454e-16] 43 [ 3.49490007e-01 8.45685660e-02 -1.38203855e-01 5.36352895e-02 44 -2.11286151e-01 2.64921441e-01] 45 [-1.51435313e-01 -4.76836971e-01 6.92423635e-01 -2.15586664e-01 46 -5.40988322e-01 3.25401658e-01] 47 [ 1.00000000e+00 -5.00000000e-01 5.00000000e-01 -7.21644966e-16 48 5.00000000e-01 -5.00000000e-01] 49 [-2.34358872e-01 -8.45857353e-01 -2.26824169e-01 1.07268152e+00 50 4.61183041e-01 6.11498480e-01]] 51 #默认返回的是按特征值升序,上下调转一下 52 V =tmp[::-1] = [[-2.34358872e-01 -8.45857353e-01 -2.26824169e-01 1.07268152e+00 53 4.61183041e-01 6.11498480e-01] 54 [ 1.00000000e+00 -5.00000000e-01 5.00000000e-01 -7.21644966e-16 55 5.00000000e-01 -5.00000000e-01] 56 [-1.51435313e-01 -4.76836971e-01 6.92423635e-01 -2.15586664e-01 57 -5.40988322e-01 3.25401658e-01] 58 [ 3.49490007e-01 8.45685660e-02 -1.38203855e-01 5.36352895e-02 59 -2.11286151e-01 2.64921441e-01] 60 [-3.33066907e-16 -3.33066907e-16 4.16333634e-16 -3.33066907e-16 61 -3.88578059e-16 1.66533454e-16]] 62 #sigma = 特征值开根号 63 #使特征值降序排序 64 S =sqrt(e)[::-1]= [1.59972303 1.41421356 1.08387677 0.51584626 nan] 65 #特征向量归一化 66 for i in range(V.shape[1]): 67 V[:, i] /= S 68 ----------------------------------------------------------------------------- 69 V = [[-1.46499655e-01 -5.28752375e-01 -1.41789650e-01 6.70542025e-01 70 2.88289305e-01 3.82252720e-01] 71 [ 7.07106781e-01 -3.53553391e-01 3.53553391e-01 -5.10280049e-16 72 3.53553391e-01 -3.53553391e-01] 73 [-1.39716356e-01 -4.39936516e-01 6.38839814e-01 -1.98903298e-01 74 -4.99123458e-01 3.00220160e-01] 75 [ 6.77508074e-01 1.63941415e-01 -2.67916753e-01 1.03975338e-01 76 -4.09591321e-01 5.13566659e-01] 77 [ nan nan nan nan 78 nan nan]] 79 S = [1.59972303 1.41421356 1.08387677 0.51584626 nan]
6.2 列数不大于行数时
1 1 #初始化数组X 2 2 X = [[ 1 3] 3 3 [ 4 7] 4 4 [ 3 2] 5 5 [ 1 23]] 6 6 num_data, dim = X.shape 7 7 X.shape= (4, 2) 8 8 U, S, V = linalg.svd(X) 9 9 U.shape, S.shape, V.shape=(4, 4) (2,) (2, 2) 10 10 V = [[ 0.10462808 0.99451142] 11 11 [ 0.99451142 -0.10462808]] 12 12 V = V[:dim] #V = V[:dim] or V =V[:num_data] ??? 注意:此时num_data > dim,所以我认为应该是V[:dim] 13 13 V[dim-1] =V[ 1 ]= [ 0.99451142 -0.10462808] 14 14 #计算结果 15 15 U = [[ 0.12635702 0.149642 -0.4064109 -0.89245244] 16 16 [ 0.30196809 0.71358512 -0.49810453 0.38923441] 17 17 [ 0.09422707 0.60994996 0.75324035 -0.22740114] 18 18 [ 0.94019702 -0.31042648 0.13910799 0.0177182 ]] 19 19 S = [24.43997403 4.54836997] 20 20 V = [[ 0.10462808 0.99451142] 21 21 [ 0.99451142 -0.10462808]]
7 环境配置
7.1 需要准备的安装包
下载python(x,y)2.7.x: http://www.softpedia.com/get/Programming/Other-Programming-Files/Python-x-y.shtml
下载PVC包:https://github.com/willard-yuan/pcv-book-code
7.2 安装Python(x, y)
在Windows下,推荐安装Python(x,y)2.7.x。Python(x,y)2.7.x是一个库安装包,除了Python自身外,还包含了第三方库,下面是安装Python(x, y)时的界面:
选择Full模式,自动安装的包见下图,
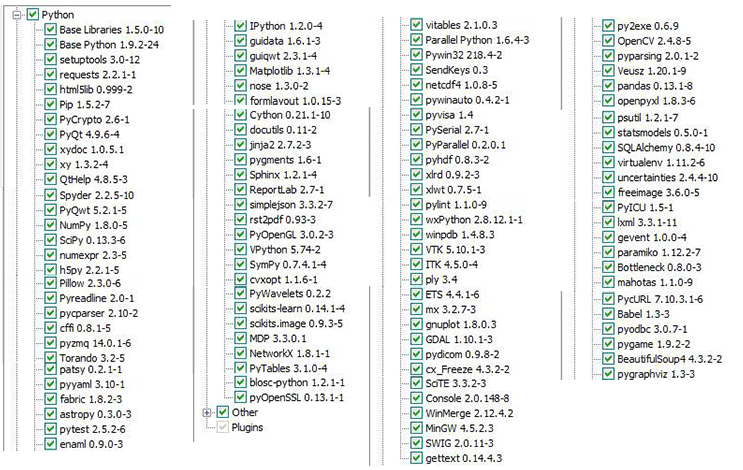
从上面第二幅图可以看出,pythonxy不仅包含了SciPy、NumPy、PyLab、OpenCV、MatplotLib,还包含了机器学习库scikits-learn。 为避免出现运行实例时出现的依赖问题,译者建议将上面的库全部选上,也就是选择“full”(译者也是用的全部安装的方式进行后面的实验的)。安装完成后,为验证安装是否正确,可以在Python shell里确认一下OpenCV是否已安装来进行验证,在Python Shell里输入下面命令:
1 from cv2 import __version__ 2 __version__
自动安装的pyopencv有问题。需要你把opencv卸载后重新安装就可以了。 重新安装完成后,再次输入上面命令,就可以看到OpenCV的版本信息,则说明python(x,y)已安装正确。
7.2 安装PCV库
7.2.1 安装twine
cd 到对应python的scripts目录中,执行以下命令
1 pip install twine
或者
2 python3 -m pip install twine
7.2.2 PVC的安装
PCV库是一个第三方库。安装PVC之前必须安装twine,否则安装会出错。假设你已从上面网址上下载了中译版源码,从Windows cmd终端
进入PCV所在目录:
1 cd PCV 2 python setup.py install
运行上面命令,即可完成PCV库的安装。为了验证PCV库是否安装成功,在运行上面命令后,可以打开Python自带的Shell,在Shell输入:
1 import PCV
如果未报错,则表明你已成功安装了该PCV库。
8 图像处理案案例
8.1 图像处理测试代码
1 # -*- coding: utf-8 -*- 2 import pickle 3 from PIL import Image 4 from numpy import * 5 from pylab import * 6 from PCV.tools import imtools, pca 7 8 # 获取图像列表和他们的尺寸 9 imlist = imtools.get_imlist('../data/fontimages/a_thumbs') # fontimages.zip is part of the book data set 10 im = array(Image.open(imlist[0])) # open one image to get the size 11 m, n = im.shape[:2] # get the size of the images 12 imnbr = len(imlist) # get the number of images 13 print "The number of images is %d" % imnbr 14 15 # Create matrix to store all flattened images 16 immatrix = array([array(Image.open(imname)).flatten() for imname in imlist], 'f') 17 18 # PCA降维 19 V, S, immean = pca.pca(immatrix) 20 21 # 保存均值和主成分 22 f = open('../data/fontimages/font_pca_modes.pkl', 'wb') 23 pickle.dump(immean, f) 24 pickle.dump(V, f) 25 f.close() 26 27 # Show the images (mean and 7 first modes) 28 # This gives figure 1-8 (p15) in the book. 29 figure() 30 gray() 31 subplot(2, 4, 1) 32 axis('off') 33 imshow(immean.reshape(m, n)) 34 for i in range(7): 35 subplot(2, 4, i+2) 36 imshow(V[i].reshape(m, n)) 37 axis('off') 38 show()
8.2 文件目录相对位置
data与执行文件的相对位置:
待处理图片.jpg的位置
8.3 执行结果
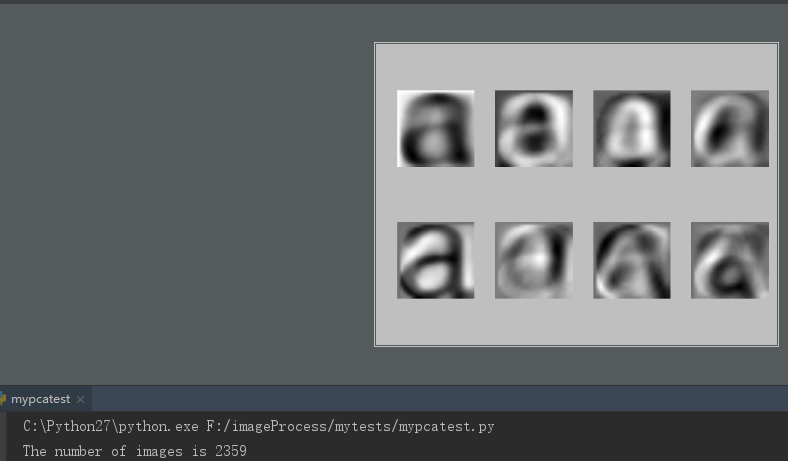
参考资料:http://yongyuan.name/pcvwithpython/installation.html