Naive Bayes 朴素贝叶斯
Scatter plot 散点图
Decision Surface Linea 决策线
朴素贝叶斯 是一个常见的寻找决策面的算法
Bayes Rule 贝叶斯规则
无人驾驶汽车是一个重要的监督分类(supervised classification)问题
监督:表示你有许多样本,我们可以说,你了解这些样本的正确答案
Acerous 还是 Non-Acerous?
机器学习主要是从实例中学习,给机器举一大堆案例,每个案例都有许多特征和属性,
如果可以挑出正确的特征,它会给你正确的信息,然后就可以对新的案例进行分类
如何利用机器学习算法来正确处理这类问题?
监督式分类示例
- □ 拿一册带标签的照片,试着认出照片中的某个人
- □ 对银行数据进行分析,寻找异常的交易,将其标记为涉嫌欺诈
- □ 根据某人的音乐喜好以及其所爱音乐的特点,比如节奏或流派推荐一首他们可能会喜欢的歌
- □ 根据优达学城学生的学习风格,将其分成不同的组群
第一个是的,第二个不是,因为并没有给出异常交易的明确定义,第三个是,第四个不是,属于聚类问题
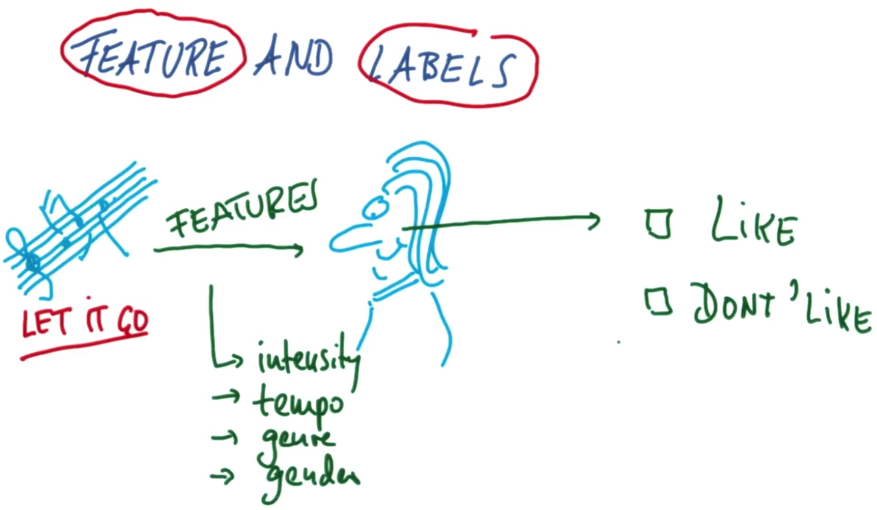
特征和标签音乐示例
Features & Labels 特征和标签
在机器学习中,我们通常会把特征作为输入,然后尝试生成标签
比如你听一首歌,它的特征可能是强度、歌曲节奏或者流派或声音性别等信息
然后你的大脑会将它处理为两个类别中的一个喜欢或者不喜欢
从散点图到决策面
机器学习算法能做什么呢?它们可以定义决策面 scatter plot decision surface
决策面通常位于两个不同的类之间的某个位置上
良好的线性决策面
当决策面为直线的时候,我们称它为线性决策面
机器学习算法所做的是 获取数据->并将其转化成一个决策面(D.S)
转为使用朴素贝叶斯
Naive Bayes 是一个常见的寻找这样的决策面的算法

Python 中的 NB 决策边界
Sklearn 使用入门
scikit-learn,经常缩写为sklearn
高斯朴素贝叶斯示例
Google 搜索 sklearn navie bayes
打开链接http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html
>>> import numpy as np >>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) >>> Y = np.array([1, 1, 1, 2, 2, 2])
#上面的代码是用来生成一些可以利用的训练点 >>> from sklearn.naive_bayes import GaussianNB
#把外部模块引入你编写的代码里 >>> clf = GaussianNB()#创建分类器,把GaussianNB赋值给clf(分类器) >>> clf.fit(X, Y)#fit替代了train,这里是我们实际提供训练数据的地方
#它会学习各种模式,然后就形成了我们刚刚创建的分类器(clf)
#我们在分类器上调用fit函数,接下来将两个参数传递给fit函数,一个是特征x一个是标签y
#在监督分类中这个过程都是如此,先调用fit函数,然后依次获得特征和标签 GaussianNB(priors=None)
#最后我们让已经完成了训练的分类器进行一些预测,我们为它提供一个新点[-0.8,-1]
#我们系那个知道的是,这个特定点的标签是什么?它属于什么类? >>> print(clf.predict([[-0.8, -1]])) [1] >>> clf_pf = GaussianNB() >>> clf_pf.partial_fit(X, Y, np.unique(Y)) GaussianNB(priors=None) >>> print(clf_pf.predict([[-0.8, -1]])) [1]
必须先训练好分类器,才能调用分类器上的预测函数。因为使用数据训练的过程是它实际学习模式的过程
然后分类器能利用学得的模式进行预测
在刚才的计算NB准确性示范例子中执行的其中一项操作,在两个不同的数据集上进行测试和训练,你自己
可能都没有主要到,实际上,在机器学习的过程中始终都是在训练,并在不同数据上测试非常重要
如果你不这样做,可能会与训练数据过拟合,可能会高估你对情况的了解程度
这非常重要,因为在机器学习中,你需要泛化在某些方面存在差别的新数据,一个算法如果只是记住所有数据
使用相同数据u作为训练数据进行测试,这样就能始终获得100%的正确率,但它不知道如何泛化新数据
我们应该始终执行并且会始终执行的操作是保存10%的数据,并将其用作测试集
你将通过这些数据真正了解你在学习数据模式方面的进展,因为它能更好、更公平地了解数据在训练时的表现
使用贝叶斯规则将 NB 拆包
刚刚构建了一个有趣的分类器,而且它可以使用,不过,现在我们要做一些深入探讨,我们要仔细分析,
算法的每个细节部分
贝叶斯规则
(概率推理的圣杯)holy grail of probabilistic inference,它被称为贝叶斯规则(Bayes rule)
癌症测试
假如一种特定癌症发生率为人口的1%,对于这种癌症的检查,
若得了这种特定癌症,检查结果90%可能是呈阳性的--这通常叫做测试的敏感性(sensitivity)
但是有时候你并没有患癌症,检查结果还是呈阳性
所以我们假设,若你没患上这种特定癌症,有90%的可能性是成阴性 -- 这通常叫做特异性(specitivity)
问题:
没有任何症状的情况下你进行了检查,检查结果成阳性
你认为患上这种特定癌症的可能性是多少?
回答:
画图,假设这是所有人和一部分人,其中只有1%患有癌症99%没有
有一个检查会告诉你是否患有癌症,正确诊断率为90%的可能性,如果画出来的话,
这部分就是患有癌症且检查结果呈阳性的,这里,这个圈是癌症患者中的90%,然而这并不是全部真相
即使这个人没有患癌症,检查结果也可能呈阳性,事实上,其几率正好是所有案例中的10%

如果癌症先验概率为1%,敏感性和特异性为90%,癌症测试结果呈阳性的人患病的概率有多大?
通过阳性测试,你就知道你在这个区域,有癌症并被检测呈阳性+没有癌症并被检测呈阳性
但是在这个圆圈内部,癌症区域的比例,与整个区域比起来还是非常小
它会变大,很显然阳性测试改变了癌症概率,但是它只增加到大约8倍
先验和后验
贝叶斯法则的本质:

这里有一些被称为先验的概率,也就是你在检测之前所得到的概率(prior probability)
然后你会从测试本身获得一些证据(evidence),
这些都是会引导你获取后验概率(posterior probability)
贝叶斯法则 是将测试中的某些证据加入你的先验概率以便获得后验概率
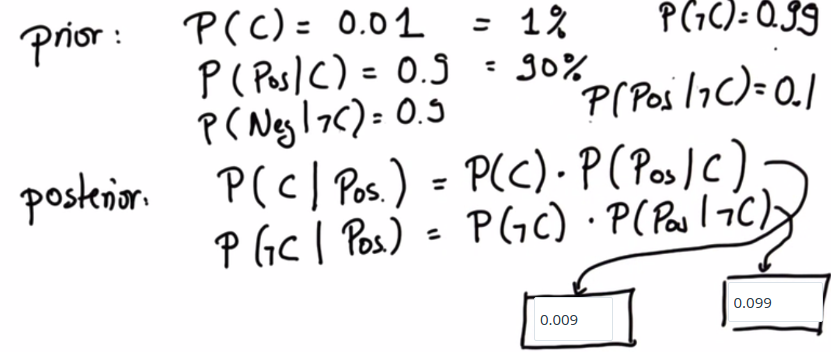
在上面的癌症示例中,我们知道 癌症的先验概率是0.01,也就是1%
在检验结果是阳性的情况下(这里我们简称为阳性) 患癌症的概率
是先验概率乘以我们检测的敏感性(敏感性也就是在患有癌症的情况下阳性的概率)
你可能还记得,该敏感性是0.9或90%。为了让这个结果准确,我们还需要非癌症的后验概率
Posterior 应该写为:
P(C, Pos) = P(C) • P(Pos|C)
P(ℸC, Pos) = P(ℸC)• P(Pos|ℸC)
这里的结果是在阳性的情况下没有患癌症的概率,这里使用了先验概率,我们知道非癌症的概率为0.99
乘以非癌症的情况下阳性的概率。这两个方程的表达方式相同,但是癌症换成了非癌症
我们知道如果没有癌症,测试得出阴性结果的几率为90% ,那么没有癌症得出我们阳性结果的几率为10%
更有趣的是,这是一个大概正确的方程 ,只是概率加起来还不到1
规范化
归一化分为2步:我们只需要把这些数字归一,比例保持不变,但是确保它们相加之和为1
首先,让我们计算这两个数字的和,0.099+0.009 = 0.108
严格地说,它的真正含义是阳性测试结果的概率

第二步是现在我们终于提到了另外的这一个后验概率,之前的后验概率通常被称之为两个事件的联合概率(joint)。而且这个后验概率是通过这个数除以规范化值得到的

贝叶斯规则图

我们所说的情况中包括了一个先验概率(prior),一项测试(test)和它的敏感性(sensitivity)
和特殊性(specificity)
比如说,如果你得到一个阳性(positive)测试结果,你要做的是获取先验结果,
然后把此测试结果的概率分别乘以(multiply),在C发生的情况(P(Pos|C))
和在C不发生(P(Pos|!C))的情况下,获取相应检验结果的概率
左边就是考虑你患癌症的分支 ,右边就是考虑你未患癌症的分支
完成此操作后,你将得到一个数字,左边是该数字把患癌症(P(Pos,C))假设和测试结果结合了起来,
右边包含了未患病假设(P(Pos,!C)),现在我们将这些结果相加,它们的结果通常不会超过1
你会得到一个数量,这刚好是测试结果在总样本中的概率(P(Pos)在本例中为阳性)
接下来,你只需要把左边的结果除以(divide)这里的总和,也叫做归一化(normalize),
在右边也执行同样的操作,两种情况下的除数都相同,
因为这是你的患病范围、未患病范围。但是P(Pos)这个值将不再以来癌症变量
你现在得出的是所需的后验概率P(C|Pos)
如果你按此处所示正确执行了所有操作,它们相加的和将为1。这就是贝叶斯规则算法(Bayes Rule)
用于分类的贝叶斯规则
可以在很多方面使用贝叶斯规则,其中一个是用于Text Learning
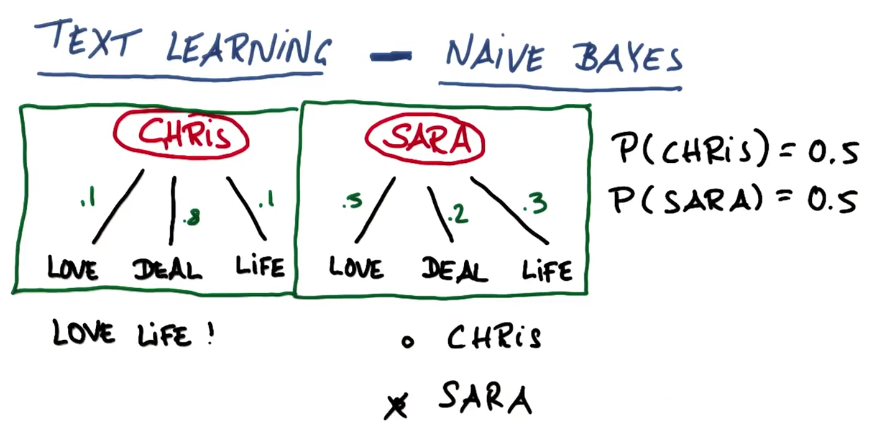
假设我们有两个人,其中一个叫Chris另一个叫Sara,而且两个人都写了很多电子邮件
为了简单起见,假设这些邮件仅包含3个词语,它们包括 爱(love)、交易(deal) 和生活(life)
Chris和Sara的区别是他们使用这些词语的频率不同,为了简单起见,假设Chris喜欢谈论交易(deal)
那么他的词语中有80%或0.8涉及交易,且他谈及生活和爱的概率为0.1
Sara更多的谈及爱,较少的谈及交易和生活,分别占0.2和0.3
现在可以使用朴素贝叶斯方法基于随机邮件确定邮件的发送人
----------------------------------------------------------------------
假设有一封电子邮件谈及爱和生活,不知道是谁发送的,但是希望弄清楚发送人是谁
假设事先认定发送人是Chris或Sara的概率各为50%
可以使用基本形式判断,因此我们会说Chris的概率等于0.5,这意味着发送人是Chris的先验概率为50%
那么Sara的概率也是0.5,所以,直观的来看,谁更可能写了这封电子邮件呢?

后验概率 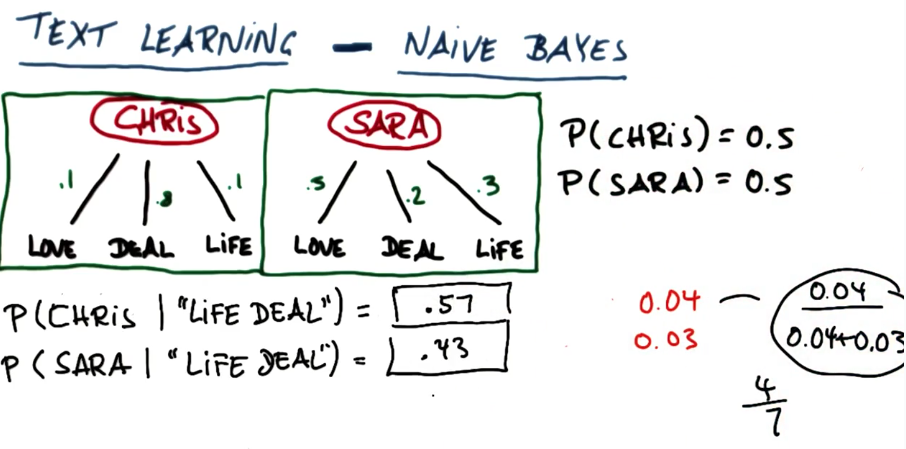
为何朴素贝叶斯很朴素
跟平常监督学习中的情况一样,它能让你从文本源中鉴别这个标签更有可能

可以使用这个方法判断人或新闻资源,比如可以问,这篇文章是莎士比亚还是其他人写的
之所以叫做朴素贝叶斯是因为它忽略了一件事,词序,因为这个乘积没有考虑词序
而英语是有词序的,如果随意将单词重新排序,那句子是没有任何意义的
没有注意到词序,所以它并没有真正理解这个文本,它只能把词的频率当成一种分类方法
这就是为什么被称为Naive(朴素)的原因
朴素贝叶斯的优势和劣势
优势:1、非常易于执行 2、它的特征空间非常大在两万-二十万英文单词之间3、运行非常容易,非常有效
缺点:1、它会与间断,由多个单词组成且意义明显不同的词语不太适合(芝加哥公牛)
具体根据想要解决的问题,以及必须要解决的数据集,不可以把监督分类算法当作黑匣子
而是把它们当作成一种理论性理解关于算法如何运行,以及是否适合你想要解决的问题,当然需要进行测试
之前谈的训练集测试集,以及可以检查测试集的表现以及它是如何运行的
如果表现的不尽如意,它可能就是错误的算法或者是错误的参数