bzoj 3246 [ioi2013]Dreaming 贪心

有n个点，由m条边连接，第i条边的边权是wi。这些点和边构成了一个森林。你必须要新建若干条条权值为W天的边，使得原图恰好变成一棵树，并且让任意两个点间最长距离最短。求该通行时间
思路：
首先找出每棵树的直径和中心及其对应半径。
加边的过程一定是在这些中心之间加边。
考虑这些中心的连接方式。
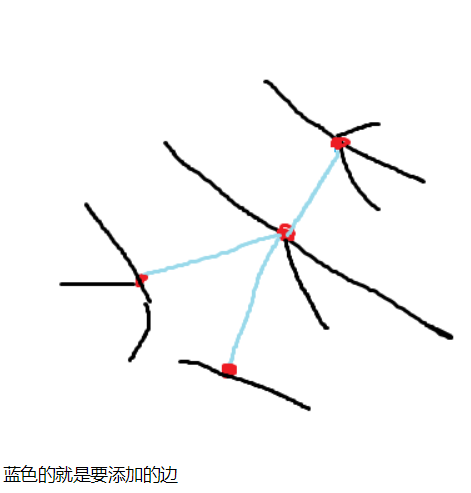
选择一个中心，让其它中心都直接连上这个点肯定是最优的，中心点为最大半径所在的那个点。
则答案要么是原树中的直径，要么是加边以后的新的直径。
新的直径分两种情况，一种是最大半径和次大半径直径直接用一条新边相连，另一种是次大边和第三大边用两条新边相连。

更简单的做法是：将中心点与其它点的半径点连边，在原图上哟，然后跑一次新树的直径。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;

const int N = 500010;
int n, m, cnt;
LL w, r, ans;
int head[N], son[N];
LL f[N], g[N];
bool vis[N];
struct Edge
{
    int to, nex; LL v;
    Edge() {}
    Edge(int x, int y, LL z) { to = x, nex = y, v = z; }
}e[N<<1];

inline void addEdge(int x, int y, LL z)
{ e[++ cnt] = Edge(y, head[x], z); 
head[x] = cnt; 
}
inline void dfs(int u, int lst) //找出以u为根时，每个点的最长链及次长链 
{
    vis[u] = 1; 
    f[u] = g[u] = 0;
    for(int i = head[u]; i; i = e[i].nex) 
    {
        int v = e[i].to; 
        if(v == lst) continue;
        dfs(v, u);
        if(f[v]+e[i].v > f[u]) 
        son[u] = v, f[u] = f[v]+e[i].v;
    }
    for(int i = head[u]; i; i = e[i].nex)
        if(e[i].to != lst && e[i].to != son[u]) 
            if(f[e[i].to]+e[i].v > g[u]) 
                 g[u] = f[e[i].to]+e[i].v;
}
inline void dfs2(int u, int lst, LL d)
//u代表当前点,lst代表其父亲点,d代表距离
//采用换根法求出每个点到其它点的最长链及次长链 
{
    if(d > f[u]) 
         g[u] = f[u], f[u] = d, son[u] = lst;
    else 
        if(d > g[u]) 
          g[u] = d;
    r = min(r, f[u]); //r代表树的半径，其为所有点的最长链的最小值 
    ans = max(ans, f[u]);//必然会找到某个叶子点，其最长链即为这个树的直径 
    for(int i = head[u]; i; i = e[i].nex) 
    if(e[i].to != lst) 
    {
        if(e[i].to != son[u]) 
               dfs2(e[i].to, u, f[u]+e[i].v);
        else 
            dfs2(e[i].to, u, g[u]+e[i].v);
    }
}
int main()
{
    scanf("%d%d%lld", &n, &m, &w);
    for(int i = 1; i <= m; i ++) 
    {
        int x, y; LL z; 
        scanf("%d%d%lld", &x, &y, &z);
        x ++, y ++; 
        addEdge(x, y, z); addEdge(y, x, z);
    }
    LL mx = -1e18,mx2 = -1e18, mx3 = -1e18;//这边一定要赋最小，-1e9也没用。
    for(int i = 1; i <= n; i ++) 
    if(!vis[i]) 
    {
        r = 1e18; 
        dfs(i, 0); 
        dfs2(i, 0, 0);
        //求出每个树的半径后，求所有半径的最长，次长，及第三长 
        if(r > mx) mx3 = mx2, mx2 = mx, mx = r;
        else if(r > mx2) mx3 = mx2, mx2 = r;
        else if(r > mx3) mx3 = r;
    }
    ans = max(ans, mx+w+mx2);
    ans = max(ans, mx2+mx3+w+w);
    printf("%lld\n", ans);
    return 0;
}