Krustal重构树

zz:https://blog.csdn.net/ouqingliang/article/details/81206050

Kruskal重构树基于Kruskal算法。在执行算法过程中，Kruskal算法会把u,v两点所在的连通块连一条边。而这里会
新建一个节点，点权为原来的图中这条边的边权，并把此节点与u,v的祖先分别连边。最终便会得到一棵Kruskal重
构树。
很明显有如下结论：
1，这是一棵二叉树；
2，叶子节点代表原图的点，非叶子节点表示原图的一条边；
3，对于所有非叶子节点，其点权<父亲节点的点权。举个栗子：

原图:

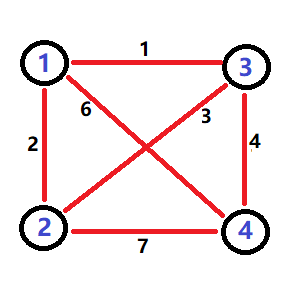
重构树

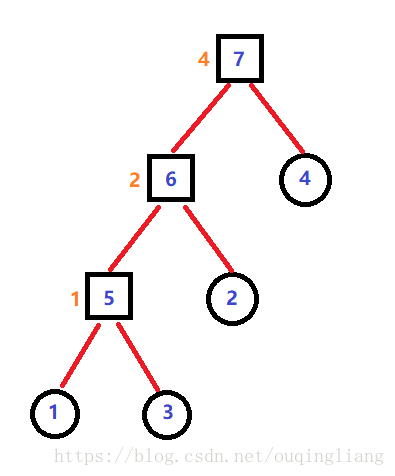
例题：BZOJ3732（Network）

题意：给定一个图，对于每个询问求u到v的所有路径中，边的最大值最小多少？

分析：Kruskal重构树模板题。每个询问实际上就是询问在最小生成树中的u,v之间的路径的最大值。

对结论3扩展一下，可以知道：lca(u,v)的点权即为所求。

时间复杂度O(N*logN)

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
using namespace std;
#define N 15010
int n,m,k,num,logn;
struct Edge{
    int x,y,val;
};
bool operator < (const Edge a,const Edge b)
{
	return a.val<b.val;
}
Edge e[N<<1];
int fa[N<<1];
int find(int x)
{
	return (fa[x]==x)?x:fa[x]=find(fa[x]);
}

vector<int> tr[N<<1];
void AddEdge(int x,int y) 
{
	tr[y].push_back(x);
}

int dep[N<<1];
int f[N<<1][20];
int w[N<<1];
void dfs(int pre,int u)
//从u点开始dfs,pre为其父亲点 
{
    dep[u] = dep[pre]+1;
    f[u][0] = pre;
    for(int i=1;i<=logn && f[u][i-1];i++)
        f[u][i] = f[f[u][i-1]][i-1];

    int len = tr[u].size();
    for(int i=0;i<len;i++)
        dfs(u,tr[u][i]);
}

int lca(int u,int v)
{
    if(dep[u]<dep[v]) swap(u,v);
    for(int i=logn;i>=0;i--)
        if(dep[f[u][i]] >= dep[v])
            u = f[u][i];
    for(int i=logn;i>=0;i--)
        if(f[u][i] != f[v][i])
        {
            u = f[u][i]; v = f[v][i];
        }
    if(u!=v) u = f[u][0];
    return u;
}

int main()
{
    scanf("%d%d%d",&n,&m,&k); 
	num = n;
    for(int i=1;i<=m;i++) 
	scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].val);
    sort(e+1,e+m+1);
    for(int i=1;i<=(n<<1);i++) 
	fa[i] = i;
    int fx,fy;
    for(int i=1,sum = 0;i<=m&&sum<n-1;i++)//建重构树 
    {
        fx = find(e[i].x); 
		fy = find(e[i].y);
        if(fx != fy)
        {
            w[++num] = e[i].val;
            fa[fx] = fa[fy] = num;
            AddEdge(fx,num); 
			AddEdge(fy,num);
            sum++;
        }
    }
    logn = log(num)/log(2);
    int x,y;
    dfs(0,num);//在重构树上跑次dfs,后面再来求lca 
    while(k--)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",w[lca(x,y)]);
    }
    return 0;
}