Snow的追寻--线段树维护树的直径

Snow终于得知母亲是谁，他现在要出发寻找母亲。王国中的路由于某种特殊原因，成为了一棵有n个节点的根节点
为1的树，但由于"Birds are everywhere."，他得到了种种不一样的消息，每份消息中都会告诉他有两棵子树是禁
忌之地，于是他向你求助了。他给出了q个形如"x y"的询问，表示他不能走到x和y的子树中，由于走的路径越长他
遇见母亲的概率越大但是他只能走一条不经过重复节点的路径，现在他想知道对于每组询问他能走的最长路径是多
少，如果没有，输出零。
第一行两个正整数n和q（1≤n,q≤100000）
第二到第n行每行两个整数u,v表示u和v之间有一条边连接，边的长度为1。
接下来q行每行两个x,y表示一组询问，意义如题目描述。
1≤n≤100000，1<=q<=50000
Output
q行，输出见题目描述
Sample Input
5 2
1 3
3 2
3 4
2 5
2 4
5 4
Sample Output
1
2
样例解释
询问1中2和4的子树不能走，最长路径为(1,3)长度为1
询问2中5和4的子树不能走，最长路径为(1,3,2)长度为2

Sol:

很明显的每个询问就是在求将两棵子树去掉后剩下的树的直径。我们先可以得出该树的dfs序，那么对于一颗子树就变成了序列上的一个区间，那么我们可以用线段树，维护一个区间表示的点的直径，对于两个区间，直径的合并就是从四个端点中任选两个连成的路径，选出其中长度最长的，即为合并后的直径，时间复杂度O(N*log₂N)

/*
对树进行dfs遍历，形成一个长度为N的序列。
要去掉的两个子树，在dfs序中是连续的。
从整个序列中去掉这两个序列，可能形成二个或三个连续的序列
对序列进行合并求直径。
每个序列有左右端点，形成的新的直径，有四种选择。对于端点之间的距离利用lca来求就好了。
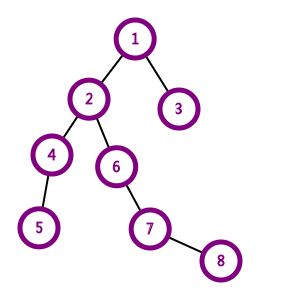
对于文后图标样例，形成一个dfs序列,其中45及78是要去掉的
12 45 6 78 3  
于是合并12 6 3这三个区间就好了 
*/
#include<cstdio>
#include<iostream>
#include<algorithm>
#define ls now<<1,l,mid
#define rs now<<1|1,mid+1,r
#define rep(i,x) for(int i=head[x],v=e[i].to;i;i=e[i].nxt,v=e[i].to)
using namespace std;
const int maxn=100010;
struct fk
{
	int to,nxt;
}
e[maxn<<1];
int cnt,n,q,tot,head[maxn],dfn[maxn],p[maxn],last[maxn],dep[maxn],f[maxn][20];
struct fq{int sum,x,y;}
t[maxn<<2],ans;
void ins(int u,int v)
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
void dfs(int x,int fa)
{
    dfn[x]=++tot;//x进入的时间点 
	p[tot]=x;//第tot个点是x 
	f[x][0]=fa;
	dep[x]=dep[fa]+1;
    rep(i,x)
	    if(v!=fa)
		    dfs(v,x);
	last[x]=tot;
}
int lca(int x,int y)
{
    if(dep[x]<dep[y])
	   swap(x,y);
    for(int i=19;i>=0;i--)
	   x=dep[f[x][i]]>dep[y]?f[x][i]:x;
    if(dep[x]>dep[y])
	    x=f[x][0];
    for(int i=19;i>=0;i--)
	    if(f[x][i]!=f[y][i])
		     x=f[x][i],y=f[y][i];
    return x==y?x:f[x][0];
}
int dis(int x,int y) //求x,y两点的距离 
{
	if(!x||!y)
	   return 0;
	int z=lca(x,y);
	    return dep[x]+dep[y]-2*dep[z];}
void merge(fq &now,fq x,fq y)
//将x,y所代表的区间进行合并，结果放到now中 
{
    int a,b,c,d,e;
    a=dis(x.x,y.x);//新直径可能为x左点与y左点的距离 
	b=dis(x.x,y.y);//新直径可能为x左点与y右点的距离
	c=dis(x.y,y.x);
	d=dis(x.y,y.y);
    e=max(a,max(b,max(c,d)));//取最大值 
    if(a==e)
	    now.x=x.x,now.y=y.x,now.sum=a;
	if(b==e)
	    now.x=x.x,now.y=y.y,now.sum=b;
    if(c==e)
	   now.x=x.y,now.y=y.x,now.sum=c;
	if(d==e)
	   now.x=x.y,now.y=y.y,now.sum=d;
    if(x.sum>now.sum)//x区间的直径大于之 
	   now.x=x.x,now.y=x.y,now.sum=x.sum;
    if(y.sum>now.sum)//y区间的直径大于之
	   now.x=y.x,now.y=y.y,now.sum=y.sum;
    if(!now.sum)
	   now.x=now.y=0;
}
void build(int now,int l,int r)
{
    if(l==r)
	 {
			t[now].x=t[now].y=p[l];
			return ;
	 }
    int mid=(l+r)>>1;
	build(ls);
	build(rs);
	merge(t[now],t[now<<1],t[now<<1|1]);
}
void get_ans(int now,int l,int r,int x,int y)
//get_ans(1,1,n,1,dfn[u]-1);
//now根结点编号,l,r左右区间 
{
    if(x<=l&&r<=y)
	  {
			merge(ans,ans,t[now]);
			return ;
	  }
    int mid=(l+r)>>1;
    if(x<=mid)
	   get_ans(ls,x,y);
    if(y>mid)
	   get_ans(rs,x,y);
}
int main()
{
    scanf("%d%d",&n,&q);
	int u,v;
    for(int i=1;i<n;i++)
	     scanf("%d%d",&u,&v),ins(u,v),ins(v,u);
    dfs(1,0);
	for(int j=1;j<20;j++)
	    for(int i=1;i<=n;i++)
		     f[i][j]=f[f[i][j-1]][j-1];
    build(1,1,n);
    while(q--)
    {
        scanf("%d%d",&u,&v);
        if(v==1||u==1) //去掉的是根结点 
		  {
				puts("0");
				continue;
		  }
        ans.sum=ans.x=ans.y=0;
        if(dfn[u]>dfn[v]) //让u进入的时间更小 
		   swap(u,v);
        get_ans(1,1,n,1,dfn[u]-1);//从1开始到u进入前的 
        get_ans(1,1,n,last[u]+1,dfn[v]-1);//从u离开后v进来之前 
        if(last[v]<=last[u])
		//看谁离开的时间更大,从离开后的那个时间到n之一段也要加进来 
		    get_ans(1,1,n,last[u]+1,n);
        else 
		     get_ans(1,1,n,last[v]+1,n);
        printf("%d
",ans.sum);
    }
}

　　

 参考下这个文章:https://blog.csdn.net/rzO_KQP_Orz/article/details/52280811