广义容斥定理入门之集合计数

zz:https://www.cnblogs.com/Parsnip/p/11530658.html

一个有N个元素的集合有2^N个不同子集（包含空集），现在要在这2^N个集合中取出若干集合（至少一个），使得

它们的交集的元素个数为K，求取法的方案数，答案模1000000007。（是质数喔~）
Input

一行两个整数N,K
1≤N≤1000000；0≤K≤N；
Output

一行为答案。
Sample Input

3 2
Sample Output

6
【样例说明】
假设原集合为{A,B,C}
则满足条件的方案为：{AB,ABC},{AC,ABC},{BC,ABC},{AB},{AC},{BC}

当这些集合具有一个元素的交集的时候，我们就认为这种方案具有一个性质，那么我们要求的就是具有kk个性质的元素个数，是广义容斥原理计算的对象。
那么我们现在只需考虑如何计算至少具有kk个性质的元素个数即可。
首先，我们只要强制选kk个元素，使他们成为交集的一部分，然后剩下的随便选，这样的方案就一定具有kk个元素以上的交集。
那么就可以这样计算了：
α(k)=c(n,k)*2^(2^(n−k))
组合意义：首先我们选k个元素有c(n,k)种方案，剩下的元素可选可不选，可以组成2^(n−k)个子集，每个子集可选可不选，就有2^(2^(n−k))种方案了。
直接使用公式计算β(k)的值即可。

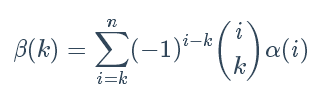
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+20 , Mod = 1e9+7;
int n,k,alpha[N],fac[N],inv[N],Pow[N],ans;
inline int add(int a,int b)
{
return a + b >= Mod ? a + b - Mod : a + b;
}
inline int mul(int a,int b)
{
return 1LL * a * b % Mod;
}
inline int sub(int a,int b)
{
return a - b < 0 ? a - b + Mod : a - b;
}
inline void Add(int &a,int b)
{
a = add( a , b );
}
inline void Mul(int &a,int b)
{
a = mul( a , b );
}
inline void Sub(int &a,int b)
{
a = sub( a , b );
}
inline int quickpow(int a,int b)
{
int res = 1;
for (;b;Mul(a,a),b>>=1)
if ( 1 & b )
Mul(res,a);
return res;
}
inline void init(void)
{
fac[0] = inv[0] = Pow[0] = 1;
for (int i=1;i<=n;i++)
fac[i] = mul( fac[i-1] , i ) , Pow[i] = Pow[i-1] * 2LL % (Mod-1);
inv[n] = quickpow( fac[n] , Mod-2 ); //暴力求n!的逆元
for (int i=n-1;i>=1;i--) //倒推，求出(n-1)!到1!的逆元
inv[i] = mul( inv[i+1] , i+1 );
}
inline int C(int n,int m)
//C(n,m)=n!/(m! * (n-m)!)
//为了消掉m!及 (n-m)!,则乘上m!的逆元及(n-m)!的逆元
{
return mul( fac[n] , mul( inv[m] , inv[n-m] ) );
}
inline void solve(void)
{
for (int i=0;i<=n;i++)
//a[i]=c(n,i) * 2^(2^(n-i))
//选择了i个元素有c(n,i)种情况 ，还有n-i个元素。它们总有2^(n-i)个子集
//每个集合可选可不选，于是又有 2^(2^(n-i)) 种可能
alpha[i] = mul( C(n,i) , quickpow( 2 , Pow[n-i] ) );
for (int i=k;i<=n;i++)
if ( ( i - k ) & 1 ) //如果是偶数项就减
Sub( ans , mul( C(i,k) , alpha[i] ) );
else //是奇数项就加
Add( ans , mul( C(i,k) , alpha[i] ) );
}
int main(void)
{
scanf("%d%d",&n,&k);
init();
solve();
printf("%d ",ans);
return 0;
}