Gty的妹子树

我曾在弦歌之中听过你，

檀板声碎，半出折子戏。

舞榭歌台被风吹去，

岁月深处尚有余音一缕……

Gty神(xian)犇(chong)从来不缺妹子……
他来到了一棵妹子树下，发现每个妹子有一个美丽度……
由于Gty很哲♂学，他只对美丽度大于某个值的妹子感兴趣。
他想知道某个子树中美丽度大于k的妹子个数。
某个妹子的美丽度可能发生变化……
树上可能会出现一只新的妹子……
维护一棵初始有n个节点的有根树(根节点为1)，树上节点编号为1-n，每个点有一个权值wi。
支持以下操作：
0 u x 询问以u为根的子树中，严格大于x的值的个数。(u^=lastans,x^=lastans)
1 u x 把u节点的权值改成x。(u^=lastans,x^=lastans)
2 u x 添加一个编号为"当前树中节点数+1"的节点，其父节点为u，其权值为x。(u^=lastans,x^=lastans)
最开始时lastans=0。

Input
输入第一行包括一个正整数n(1<=n<=30000)，代表树上的初始节点数。
接下来n-1行，每行2个整数u,v，为树上的一条无向边。
任何时刻，树上的任何权值大于等于0，且两两不同。
接下来1行，包括n个整数wi，表示初始时每个节点的权值。
接下来1行，包括1个整数m(1<=m<=30000)，表示操作总数。
接下来m行，每行包括三个整数 op,u,v：
op,u,v的含义见题目描述。
保证题目涉及的所有数在int内。

Output

对每个op=0，输出一行，包括一个整数，意义见题目描述。

Sample Input
2
1 2
10 20
1
0 1 5
Sample Output

2

Sol:

首先DFS，对于每个节点，如果这个节点的父亲节点所在块未满，就塞进父节点所在块中，否则自成一块，每一块记录块的根节点，然后与父节点所在的块的根节点连边 。

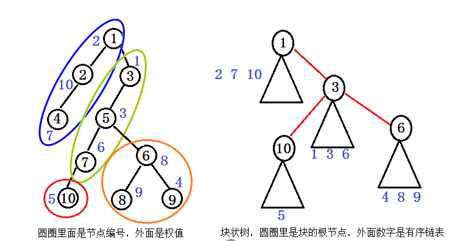
我们记录每个节点所属的块，即块的根节点，建立两个图：一个图存原树（双向边），一个图存块的连通性（单向边）。
我们维护块内的元素有序，可以用链表。
如果一个节点是第一个加入块的，那么不会有别的子树的节点属于这个块，那么我们在查询一个子树时，只需要从子树的根开始向下遍历，先处理这些不在完整块内的点，一旦我们碰到了别的块内的点，就立即转移到块的图上去跑。

例如查询5,6：5不是块的根节点，所以查询单个节点5，再查询单个节点7，再查询节点6，发现6是块的根节点，可以在用二分法在块有序链表找到>6的节点个数，再查询节点10，发现10也是块的根节点

#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N=100005;
int n,m,k,ans;
int size[N],w[N],top[N];
vector<int>list[N];

inline int read()//快速读入 
{char ch=getchar();
 int x=0,f=1;
 while (ch<'0'||ch>'9') {if(ch=='-')f=-1; ch=getchar();}
 while (ch>='0'&&ch<='9') {x=x*10+ch-'0'; ch=getchar();}
 return x*f;
}

struct Node
{int head[N],v[N],nxt[N],tot;
 void add(int x,int y) 
 {
		v[++tot]=y;nxt[tot]=head[x];head[x]=tot;
 }
}Map,Block,Link;

void dfs(int u,int f)//一遍DFS,分块 
{
 int root=top[u];//top[u]记录u所在块的根节点 
 list[root].push_back(w[u]);//同一块内的节点权值放入一个链表中 
 for (int i=Map.head[u];i;i=Map.nxt[i])
   {
		if (Map.v[i]==f) continue;
        Block.add(u,Map.v[i]);//记录u到v的单向边 
        if (size[root]<k)//当前块的节点个数未满 
            size[root]++,top[Map.v[i]]=root;
        else
              Link.add(root,Map.v[i]);//Link记录块的根节点之间的关系 
        dfs(Map.v[i],u);
   }
}

void query_block(int u,int x)
{if (u==top[u])//整块查询 
   {
		ans+=list[u].end()-upper_bound(list[u].begin(),list[u].end(),x);//二分法在块的有序链表中查询>x的节点个数 
        for(int i=Link.head[u];i;i=Link.nxt[i])
	           query_block(Link.v[i],x);
   }
 else//块中零散节点查询
   {
		if (w[u]>x) ans++;
        for(int i=Block.head[u];i;i=Block.nxt[i])
               query_block(Block.v[i],x);
   }
}

void Init()
{
 int u,v,i;
 n=read();
 k=(int)sqrt(n);
 for(i=1;i<n;i++)
   {
		u=read(); 
		v=read();
        Map.add(u,v); 
		Map.add(v,u);
   }
 for(i=1;i<=n;i++)
   w[i]=read(), top[i]=i, size[i]=1;
 dfs(1,0);
 for(i=1;i<=n;i++)
   if(top[i]==i) 
       sort(list[i].begin(),list[i].end());//同一块内的节点权值链从小到大排序 
}

void Work()
{int opt,u,x,tp,last=0;
 m=read();
 while (m--)
   {opt=read(),u=read()^last,x=read()^last;
    if(opt==0)
	  {
	   ans=0;
       query_block(u,x);
       printf("%d
",last=ans);
      }
    else
	  if(opt==1) // 把u节点的权值改成x
	    {
		 tp=top[u];
         list[tp].erase(lower_bound(list[tp].begin(),list[tp].end(),w[u]));
         list[tp].insert(lower_bound(list[tp].begin(),list[tp].end(),x),x);
         w[u]=x;
        }
      else
	    {
		 w[++n]=x;
         tp=top[u];
         Block.add(u,n);
         if (size[tp]<k)//块中节点个数不满 
		   {top[n]=tp;
            size[tp]++;
            list[tp].insert(lower_bound(list[tp].begin(),list[tp].end(),x),x);
           }
         else//块中节点个数满了 
		   {top[n]=n;
            size[u]=1;
            list[n].push_back(x);
            Link.add(tp,n);
           }
        }
   }
}

int main()
{
 Init();
 Work();
 return 0;
}