lxhgww最近迷上了一款游戏,在游戏里,他拥有很多的装备,每种装备都有2个属性,这些属性的值用[1,10000]之间的数表示。当他使用某种装备时,他只能使用该装备的某一个属性。并且每种装备最多只能使用一次。 游戏进行到最后,lxhgww遇到了终极boss,这个终极boss很奇怪,攻击他的装备所使用的属性值必须从1开始连续递增地攻击,才能对boss产生伤害。也就是说一开始的时候,lxhgww只能使用某个属性值为1的装备攻击boss,然后只能使用某个属性值为2的装备攻击boss,然后只能使用某个属性值为3的装备攻击boss……以此类推。 现在lxhgww想知道他最多能连续攻击boss多少次?
Input
输入的第一行是一个整数N,表示lxhgww拥有N种装备 接下来N行,是对这N种装备的描述,每行2个数字,表示第i种装备的2个属性值
Output
输出一行,包括1个数字,表示lxhgww最多能连续攻击的次数。
Sample Input
3
1 2
3 2
4 5
Sample Output
2
HINT
【数据范围】
对于30%的数据,保证N < =1000
对于100%的数据,保证N < =1000000
极简题解:
一条边上的两个数字,优先让小数字打上标志。
如果小数字已打上了,再让大数字来打。
于是对于(a,b)来说,如果a<b,则较大的数字b,暂时不能打标记
但再个(b,c),且b<c,则b就不是目前最大的数字了,C才是最大的数字,于是b也可以打上标记了。
这正好符合并查集的传递性。
Sol:
这个题还是挺有意思的,思想用贪心和并查集。
对于连接u,v的边。
因为要保证攻击从1开始,于是我们每次用并查集去并的时候,强行让大的数字成为小的数字的父亲,并给小数字打上标志。
这样一直连下去,于是整个集合的根结点是唯一没有被打上标记的点。
于是当连接某个边,使得有环出现了,则这个时候,可以给集合的根结点打上标记了(因为整个集合只有它没打上标志了)
此时如果再来连边,就发现边的一个端点u打了标记,但另一端点v还没打上标记,于是给v也打上标记好了。
例如有以下物品时
1 2
2 3
3 4
2 5
前三个构成如下图,只有4没有被选中

对于第4个(2,5),2的父亲是4,5的父亲是5。
于是用4连5,同时标志上4,5做为父亲点,图如下:
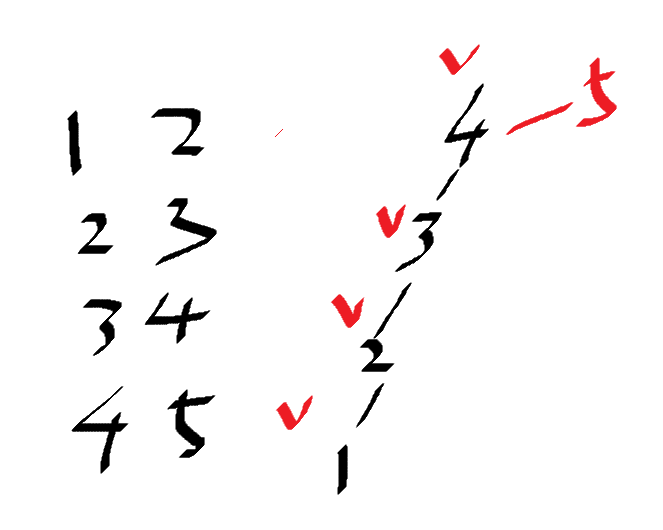
如果此时再来个物品(1,5),则发现1与5在一个集合中了。(如果是来个(2,5)也是一样的)
5是这个集合中唯一没有被标记上的,则此时就可以直接标记5了。

如果此时再来个(5,6).则发现既然5已标记上了,于是6也就可以标记上了。
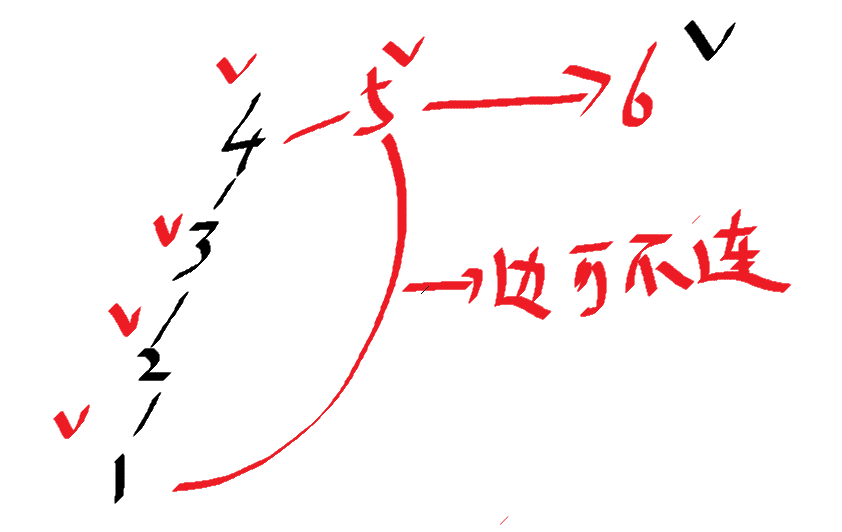
想着:并查集本质上是一种树结构
将每个装备看做边,装备属性看做点,每次合并两个点
将过程想象成给点搭配边的过程
这样得到的连通块有两类
1、没有环,即边数=点数-1,那么对于树内的任意n-1的点,都可以搭配一条边,
但题目要求从小到大攻击,所以先给小的搭配。也就是说,树内只有最大的点没有搭配边。
如何实现这一过程?在合并时,让小的合并到大的上面,也就是始终让树内最大的点是祖先节点
2、边数>=n,有环或有重边。
#include<bits/stdc++.h>
using namespace std;
int ans,q,n,m,f[1008001];
bool flag[1001011];
int find(int x) {
if(f[x]==x) return x;
return f[x]=find(f[x]);
}
void coco(int x,int y)
{
if(flag[x]==true)
flag[y]=true;
else
flag[x]=true;
f[x]=y;
}
void unionset(int x,int y)
{
int xx=find(x);
int yy=find(y);
if(xx>yy)
swap(xx,yy);
if(xx!=yy)
//如果不在一个集合中,此时优先给编号小的(设为xx)打上标记,如果xx打过了,就给yy打标记
coco(xx,yy);
else //如果在一个集合中,则此时集合中只有根结点没有打上标志了,于是给它打上
flag[xx]=true;
}
int main() {
scanf("%d",&n);
for(int i=1; i<=100001; i++) f[i]=i;
for(int i=1,x,y; i<=n; i++) {
scanf("%d%d",&x,&y);
unionset(x,y);
}
for(int i=1; i<=100001; i++)
if(flag[i]==false)
{
ans=i;
break;
}
printf("%d",ans-1);
return 0;
}
//wrong,这个程序对于一个环,再连一条边出来的情况,没有考虑到。
#include<cstdio>
#include<algorithm>
using namespace std;
int n,fa[10001];
bool v[10001];
int find(int i)
{
return fa[i]==i ? i:fa[i]=find(fa[i]);
}
int main()
{
for(int i=1;i<=10000;i++) fa[i]=i;
scanf("%d",&n);
int a,b,r1,r2;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&a,&b);
r1=find(a);r2=find(b);
if(r1==r2) v[r1]=true;
else
{
if(r1>r2) swap(r1,r2);
fa[r1]=r2;
v[r1]=true;
}
}
int i;
for(i=1;v[i];i++);
printf("%d",i-1);
}