查找的方法：
排序的方法：
简单的数据结构：
一、算计基础
1.1、什么是算法：
算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
简单的说，算法就是一个计算的过程，解决问题的办法。
一个算法应该具有以下七个重要的特征：
①有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；
②确切性(Definiteness)：算法的每一步骤必须有确切的定义；
③输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；
④输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；
⑤可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）；
⑥高效性(High efficiency)：执行速度快，占用资源少；
⑦健壮性(Robustness)：对数据响应正确。
1.2、时间复杂度
定义：如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，它是n的某一函数 T(n)称为这一算法的“时间复杂性”。
当输入量n逐渐加大时，时间复杂性的极限情形称为算法的“渐近时间复杂性”。
此外，一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。
计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间,时间复杂度常用大O符号（大O符号（Big O notation）是用于描述函数渐进行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。在数学中，它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项；在计算机科学中，它在分析算法复杂性的方面非常有用。）表述，使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。
大O，简而言之可以认为它的含义是“order of”（大约是）。
无穷大渐近
大O符号在分析算法效率的时候非常有用。举个例子，解决一个规模为 n 的问题所花费的时间（或者所需步骤的数目）可以被求得：T(n) = 4n^2 - 2n + 2。
当 n 增大时，n^2; 项将开始占主导地位，而其他各项可以被忽略——举例说明：当 n = 500，4n^2; 项是 2n 项的1000倍大，因此在大多数场合下，省略后者对表达式的值的影响将是可以忽略不计的。
时间复杂度的计算：
1）.一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，所以f（n）越小，算法的时间复杂度越低，算法的效率越高。
在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n！），找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。
3.常见的时间复杂度
按数量级递增排列，常见的时间复杂度有：
常数阶O(1), 对数阶O(log2n), 线性阶O(n), 线性对数阶O(nlog2n), 平方阶O(n2)， 立方阶O(n3),...， k次方阶O(nk), 指数阶O(2n) 。
其中，
1.O(n)，O(n2)， 立方阶O(n3),...， k次方阶O(nk) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度。。。。
2.O(2n)，指数阶时间复杂度，该种不实用
3.对数阶O(log2n), 线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高
例：算法：
1 for（i=1;i<=n;++i） 2 3 { 4 5 for(j=1;j<=n;++j) 6 7 { 8 9 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2 10 11 for(k=1;k<=n;++k) 12 13 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3 14 15 } 16 17 }
则有 T（n）= n^2+n^3，根据上面括号里的同数量级，我们可以确定 n^3为T（n）的同数量级
则有f（n）= n^3，然后根据T（n）/f（n）求极限可得到常数c
则该算法的 时间复杂度：T（n）=O（n^3)
时间复杂度为：O(1)
1 Temp=i; 2 i=j; 3 j=temp;
以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
时间复杂度为：O(n2)
交换i和j的内容
1 sum=0； （一次） 2 for(i=1;i<=n;i++) （n次 ） 3 for(j=1;j<=n;j++) （n^2次 ） 4 sum++； （n^2次 ）
解：T(n)=2n^2+n+1 =O(n^2)
例子
1 for (i=1;i<n;i++) 2 { 3 y=y+1; ① 4 for (j=0;j<=(2*n);j++) 5 x++; ② 6 }
解： 语句1的频度是n-1
语句2的频度是(n-1)*(2n+1)=2n^2-n-1
f(n)=2n^2-n-1+(n-1)=2n^2-2
该程序的时间复杂度T(n)=O(n^2).
时间复杂度为：O(n)
1 a=0; 2 b=1; ① 3 for (i=1;i<=n;i++) ② 4 { 5 s=a+b; ③ 6 b=a; ④ 7 a=s; ⑤ 8 }
解：语句1的频度：2,
语句2的频度： n,
语句3的频度： n-1,
语句4的频度：n-1,
语句5的频度：n-1,
T(n)=2+n+3(n-1)=4n-1=O(n).
时间复杂度为：O(log2n )
1 i=1; ① 2 while (i<=n) 3 i=i*2; ②
解： 语句1的频度是1,
设语句2的频度是f(n), 则：2^f(n)<=n;f(n)<=log2n
取最大值f(n)= log2n,
T(n)=O(log2n )
时间复杂度为：O(n3)
1 for(i=0;i<n;i++) 2 { 3 for(j=0;j<i;j++) 4 { 5 for(k=0;k<j;k++) 6 x=x+2; 7 } 8 }
解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n^3).
我们还应该区分算法的最坏情况的行为和期望行为。如快速排序的最 坏情况运行时间是 O(n^2)，但期望时间是 O(nlogn)。通过每次都仔细 地选择基准值，我们有可能把平方情况 (即O(n^2)情况)的概率减小到几乎等于 0。在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。
下面是一些常用的记法：
访问数组中的元素是常数时间操作，或说O(1)操作。一个算法如 果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。用strcmp比较两个具有n个字符的串需要O(n)时间。常规的矩阵乘算法是O(n^3)，因为算出每个元素都需要将n对 元素相乘并加到一起，所有元素的个数是n^2。
指数时间算法通常来源于需要求出所有可能结果。例如，n个元 素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。指数算法一般说来是太复杂了，除非n的值非常小，因为，在 这个问题中增加一个元素就导致运行时间加倍。不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。
时间复杂度小结：
间复杂度是用来估计算法运行时间的一个式子（单位）。
一般来说，时间复杂度高的算法比复杂度低的算法快。
常见的时间复杂度（按效率排序）
O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n2log2n)<O(n3)
不常见的时间复杂度（看看就好）
O(n!) O(2n) O(nn) …
如何一眼判断时间复杂度？
循环减半的过程O(logn)
几次循环就是n的几次方的复杂度
3、空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了，因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
一个算法的空间复杂度S(n)定义为该算法所耗费的存储空间，它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。空间复杂度(SpaceComplexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间，包括存储算法本身所占用的存储空间，算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法。算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地"进行的，是节省存储的算法，有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况。
分析一个算法所占用的存储空间要从各方面综合考虑。如对于递归算法来说，一般都比较简短，算法本身所占用的存储空间较少，但运行时需要一个附加堆栈，从而占用较多的临时工作单元；若写成非递归算法，一般可能比较长，算法本身占用的存储空间较多，但运行时将可能需要较少的存储单元。
一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。若一个算法为 递归算法，其空间复杂度为递归所使用的堆栈空间的大小，它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1，这个1表示开始进行的一次非递归调用)。算法的空间复杂度一般也以数量级的形式给出。如当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为O(log2n)；当一个算法的空间复杂度与n成线性比例关系时，可表示为O(n).若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。
时间复杂度与空间复杂度比较:
对于一个算法，其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；反之，当追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。另外，算法的所有性能之间都存在着或多或少的相互影响。因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。算法的时间复杂度和空间复杂度合称为算法的复杂度。
二、查找
列表查找：从列表中查找指定元素
输入：列表、待查找元素
输出：元素下标或未查找到元素
常见的查找方法有两种：
2.1顺序查找
从列表第一个元素开始，顺序进行搜索，直到找到为止。
查找成功时的平均查找长度为：（假设每个数据元素的概率相等） ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
当查找不成功时，需要n+1次比较，时间复杂度为O(n);
所以， 顺序查找的时间复杂度为O(n ) 。
顺序查找的实现：
1 import random 2 def improveseque(la,x): 3 la[0]=x 4 k=len(la)-1 5 while x!=la[k]: 6 k=k-1 7 return k 8 9 data=list(range(100)) 10 random.shuffle(data) 11 print(data) 12 13 while True: 14 key = int(input("input your want number")) 15 n = improveseque(data,key) 16 if n == 0: 17 print("not found!") 18 else: 19 print(key,"IS",n+1,"element")
2.2二分查找（折半查找）
从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。
说明：元素必须是有序的，如果是无序的则要先进行排序操作。
基本思想：也称为是折半查找，属于有序查找算法。用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。
复杂度分析： 最坏情况下，关键词比较次数为log2(n+1)，且 期望时间复杂度为O(log2n) ；
注： 折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要 频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。
二分查找的实现：
1 #Author:ajun 2 import random 3 def binary_search(dataset, find_num): 4 if len(dataset) > 1: 5 mid = int(len(dataset) / 2) 6 if dataset[mid] == find_num: 7 #print("Find it") 8 return dataset[mid] 9 elif dataset[mid] > find_num: 10 return binary_search(dataset[0:mid], find_num) 11 else: 12 return binary_search(dataset[mid + 1:], find_num) 13 else: 14 if dataset[0] == find_num: 15 #print("Find it") 16 return dataset[0] 17 else: 18 pass 19 #print("Cannot find it.") 20 21 data=list(range(0,100,4)) 22 print(data) 23 print(binary_search(data,30))
2.3其它查找算法
还有很多其它的查找算法，等学好了，再给大家补充出来。
1）. 插值查找
2）. 斐波那契查找
3）. 树表查找
4）. 分块查找
5）. 哈希查找
三、排序算法
在编程语言中，提到算法就会说到排序算法，下面简单的用Python跟大家探讨一下常见的算法！
排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。
我们这里说说排序就是内部排序。
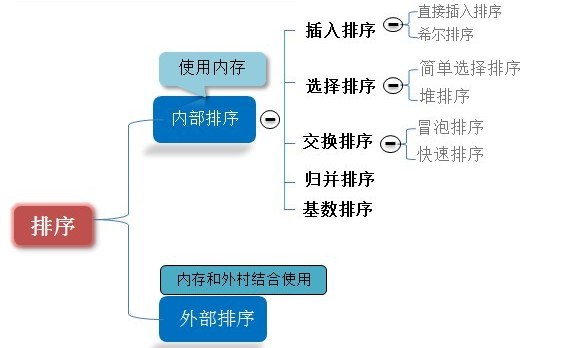
3.1插入排序—直接插入排序(Straight Insertion Sort)
基本思想:
将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。
要点：设立哨兵，作为临时存储和判断数组边界之用。
直接插入排序示例：
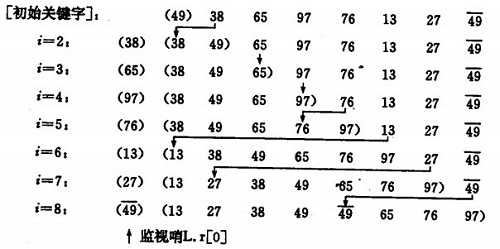
如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。
算法的实现：
1 #Author:ajun 2 import random 3 def insert_sort(li): 4 for i in range(1,len(li)): 5 tmp=li[i] 6 j=i-1 7 while j >= 0 and li[j] > tmp: 8 li[j+1]=li[j] 9 j=j-1 10 li[j+1]=tmp 11 data=list(range(100)) 12 random.shuffle(data) 13 print(data) 14 insert_sort(data) 15 print(data)
3.2选择排序—简单选择排序（Simple Selection Sort）
基本思想：
在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。
简单选择排序的示例：
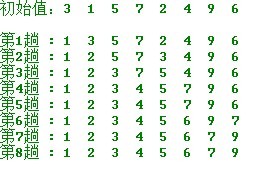
操作方法：
第一趟，从n 个记录中找出关键码最小的记录与第一个记录交换；
第二趟，从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换；
以此类推.....
第i 趟，则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换，
直到整个序列按关键码有序。
选择排序算法：
1 #Author:ajun 2 import random 3 def select_sort(li): 4 for i in range(len(li)-1): 5 min_loc=i 6 for j in range(i+1,len(li)): 7 if li[min_loc] > li[j]: 8 min_loc=j 9 li[i],li[min_loc]=li[min_loc],li[i] 10 11 data=list(range(100)) 12 random.shuffle(data) 13 print(data) 14 select_sort(data) 15 print(data)
3.3 交换排序—冒泡排序（Bubble Sort）
基本思想：
在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。
冒泡排序的示例：
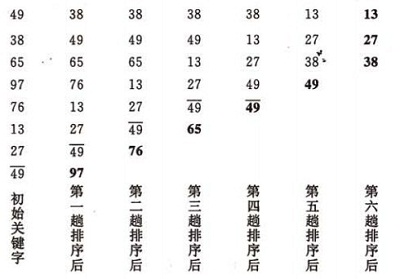
冒泡排序的实现：
1 #Author:ajun 2 import random 3 4 def bubble_sort(li): 5 for i in range(len(li)): 6 for j in range(len(li)-i-1): 7 if li[j] > li[j+1]: 8 li[j],li[j+1]=li[j+1],li[j] 9 10 data=list(range(100)) 11 random.shuffle(data) 12 print(data) 13 bubble_sort(data) 14 print(data)
3.4交换排序—快速排序（Quick Sort）
基本思想：
1）选择一个基准元素,通常选择第一个元素或者最后一个元素,
2）通过一趟排序讲待排序的记录分割成独立的两部分，其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3）此时基准元素在其排好序后的正确位置
4）然后分别对这两部分记录用同样的方法继续进行排序，直到整个序列有序。
快速排序的示例：
（a）一趟排序的过程：
（b）排序的全过程
算法的实现：
快速排序
分析：
快速排序是通常被认为在同数量级（O(nlog2n)）的排序方法中平均性能最好的。但若初始序列按关键码有序或基本有序时，快排序反而蜕化为冒泡排序。
3.5堆排序
堆排序是一种树形选择排序，是对直接选择排序的有效改进。
堆排序基础知识：（树和二叉树）
树是一种数据结构 比如：目录结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合：
如果n=0，那这是一棵空树；
如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。
一些概念：
根节点、叶子节点：
树的深度（高度）：
树的度：
孩子节点/父节点：
子树：
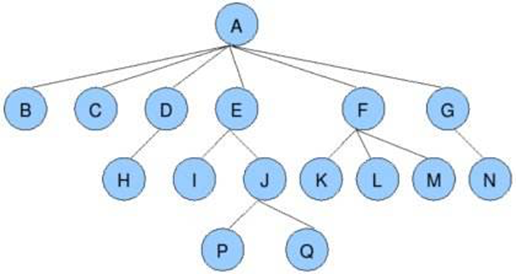
特殊的树--二叉树：
二叉树：度不超过2的树（节点最多有两个叉）
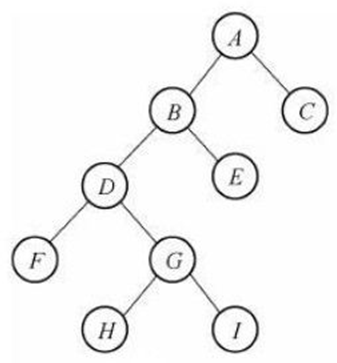
满二叉树和完全二叉树：
满二叉树是指这样的一种二叉树：除最后一层外，每一层上的所有结点都有两个子结点。在满二叉树中，每一层上的结点数都达到最大值，即在满二叉树的第k层上有2k-1个结点，且深度为m的满二叉树有2m－1个结点。
完全二叉树是指这样的二叉树：除最后一层外，每一层上的结点数均达到最大值；在最后一层上只缺少右边的若干结点。
对于完全二叉树来说，叶子结点只可能在层次最大的两层上出现：对于任何一个结点，若其右分支下的子孙结点的最大层次为p，则其左分支下的子孙结点的最大层次或为p，或为p+1。
完全二叉树具有以下两个性质：
性质5:具有n个结点的完全二叉树的深度为［log2n］+1。
性质6:设完全二叉树共有n个结点。如果从根结点开始，按层次（每一层从左到右）用自然数1，2，……，n给结点进行编号，则对于编号为k（k=1，2，……，n）的结点有以下结论：
①若k=1，则该结点为根结点，它没有父结点；若k>1，则该结点的父结点编号为INT（k/2）。
②若2k≤n，则编号为k的结点的左子结点编号为2k；否则该结点无左子结点（显然也没有右子结点）。
③若2k+1≤n，则编号为k的结点的右子结点编号为2k+1；否则该结点无右子结点。
满二叉树肯定是完全二叉树，完全二叉树不一定是满二叉树。
二叉树的存储方式：
二叉树是非线性结构，其存储结构可以分为两种，即顺序存储结构和链式存储结构。
1、顺序存储结构
---- 二叉树的顺序存储，就是用一组连续的存储单元存放二叉树中的结点。即用一维数组存储二叉树中的结点。
因此，必须把二叉树的所有结点安排成一个恰当的序列，结点在这个序列中的相互位置能反映出结点之间的逻辑关系。
用编号的方法从树根起，自上层至下层，每层自左至右地给所有结点编号。
---- 依据二叉树的性质，完全二叉树和满二叉树采用顺序存储比较合适，树中结点的序号可以唯一地反映出结点之间的逻辑关系，
这样既能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置，以及结点之间的关系。
---- 一棵完全二叉树（满二叉树）如下图所示：
将这棵二叉树存入到数组中，相应的下标对应其同样的位置，如下图所示：
但是对于一般的非完全二叉树来说，如果仍然按照从上到下、从左到右的次序存储在一维数组中，则数组下标之间不能准确反映
树中结点间的逻辑关系，可以在非完全二叉树中添加一些并不存在的空结点使之变成完全二叉树，（把不存在的结点设置为“^”）
不过这样做有可能会造成空间的浪费，如下图所示，然后再用一维数组顺序存储二叉树。
缺点是：有可能对存储空间造成极大的浪费，在最坏的情况下，一棵深度为k的右斜树，它只有k个结点，却需要2^k-1个结点存储空间。
这显然是对存储空间的严重浪费，所以顺序存储结构一般只用于完全二叉树或满二叉树。
2、链式存储结构
---- 二叉树的链式存储结构是指用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。
---- 二叉树的每个结点最多有两个孩子，因此，每个结点除了存储自身的数据外，还应设置两个指针分别指向左、右孩子结点。
结点结构如下图所示：
其中data是数据域，lchild和rchild都是指针域，分别存放指向左孩子和右孩子的指针。由上图所示的结点构成的链表称作二叉链表。
当没有孩子结点时，相应的指针域置为空。
二叉树小结：
二叉树是度不超过2的树
满二叉树与完全二叉树
（完全）二叉树可以用列表来存储，通过规律可以从父亲找到孩子或从孩子找到父亲
基本思想：
堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足
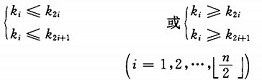
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。
大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大。
小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小。
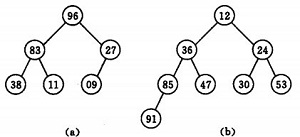
如：
（a）大顶堆序列：（96, 83,27,38,11,09)
(b) 小顶堆序列：（12，36，24，85，47，30，53，91）
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。
因此，实现堆排序需解决两个问题：
1. 如何将n 个待排序的数建成堆；
2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。
首先讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。
调整小顶堆的方法：
1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。
2）将根结点与左、右子树中较小元素的进行交换。
3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法 （2）.
4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.
5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。
称这个自根结点到叶子结点的调整过程为筛选。如图：
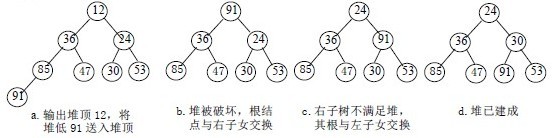
再讨论对n 个元素初始建堆的过程。
建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。
1）n 个结点的完全二叉树，则最后一个结点是第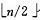
个结点的子树。
2）筛选从第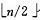个结点为根的子树开始，该子树成为堆。
3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。
如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）
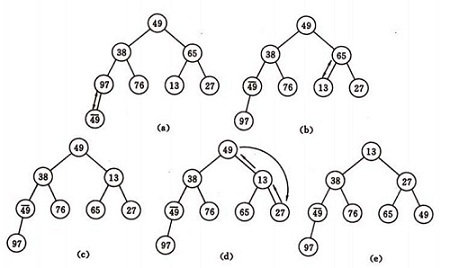
算法的实现：
从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。
1 #Author:ajun 2 import random 3 def sift(data, low, high): 4 i = low 5 j = 2 * i + 1 6 tmp = data[i] 7 while j <= high: #孩子在堆里 8 if j + 1 <= high and data[j] < data[j+1]: #如果有右孩子且比左孩子大 9 j += 1 #j指向右孩子 10 if data[j] > tmp: #孩子比最高领导大 11 data[i] = data[j] #孩子填到父亲的空位上 12 i = j #孩子成为新父亲 13 j = 2 * i +1 #新孩子 14 else: 15 break 16 data[i] = tmp #最高领导放到父亲位置 17 18 19 def heap_sort(data): 20 n = len(data) 21 for i in range(n // 2 - 1, -1, -1): 22 sift(data, i, n - 1) 23 #堆建好了 24 for i in range(n-1, -1, -1): #i指向堆的最后 25 data[0], data[i] = data[i], data[0] #领导退休，刁民上位 26 sift(data, 0, i - 1) #调整出新领导 27 28 data=list(range(100)) 29 random.shuffle(data) 30 print(data) 31 heap_sort(data) 32 print(data)
3.6归并排序
基本思想：
归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
归并排序示例：
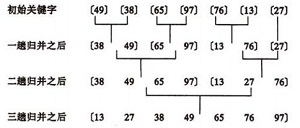
合并方法：
设r[i…n]由两个有序子表r[i…m]和r[m+1…n]组成，两个子表长度分别为n-i +1、n-m。
- j=m+1；k=i；i=i; //置两个子表的起始下标及辅助数组的起始下标
- 若i>m 或j>n，转⑷ //其中一个子表已合并完，比较选取结束
- //选取r[i]和r[j]较小的存入辅助数组rf
如果r[i]<r[j]，rf[k]=r[i]； i++； k++； 转⑵
否则，rf[k]=r[j]； j++； k++； 转⑵ - //将尚未处理完的子表中元素存入rf
如果i<=m，将r[i…m]存入rf[k…n] //前一子表非空
如果j<=n , 将r[j…n] 存入rf[k…n] //后一子表非空 - 合并结束
归并排序算法实现：
1 #Author:ajun 2 import random 3 def merge(li, low, mid, high): 4 i = low 5 j = mid + 1 6 ltmp = [] 7 while i <= mid and j <= high: 8 if li[i] < li[j]: 9 ltmp.append(li[i]) 10 i += 1 11 else: 12 ltmp.append(li[j]) 13 j += 1 14 while i <= mid: 15 ltmp.append(li[i]) 16 i += 1 17 while j <= high: 18 ltmp.append(li[j]) 19 j += 1 20 li[low:high+1] = ltmp 21 22 def _mergesort(li, low, high): 23 if low < high: 24 mid = (low + high) // 2 25 _mergesort(li,low, mid) 26 _mergesort(li, mid+1, high) 27 merge(li, low, mid, high) 28 29 def mergesort(li): 30 _mergesort(li, 0, len(li) - 1) 31 32 33 data=list(range(100)) 34 random.shuffle(data) 35 print(data) 36 mergesort(data) 37 print(data)
3.7希尔排序
希尔排序是1959 年由D.L.Shell 提出来的，相对直接排序有较大的改进。希尔排序又叫缩小增量排序
基本思想：
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。
操作方法：
- 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
- 按增量序列个数k，对序列进行k 趟排序；
- 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
希尔排序的示例：
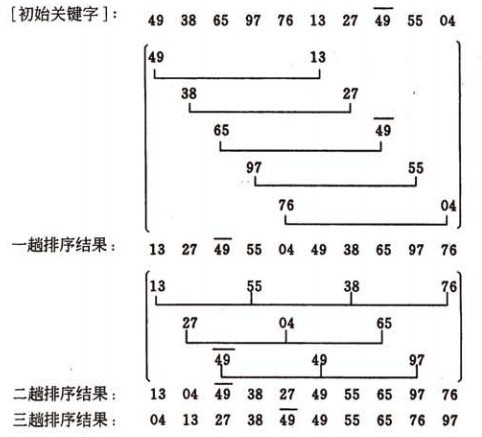
算法实现：
我们简单处理增量序列：增量序列d = {n/2 ,n/4, n/8 .....1} n为要排序数的个数
即：先将要排序的一组记录按某个增量d（n/2,n为要排序数的个数）分成若干组子序列，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。继续不断缩小增量直至为1，最后使用直接插入排序完成排序。
希尔排序的实现：
1 #Author:ajun 2 import random 3 def shell_sort(li): 4 gap=int(len(li)/2) 5 while gap >=1: 6 for i in range(gap,len(li)): 7 tmp=li[i] 8 j=i-gap 9 while j >= 0 and li[j] > tmp: 10 li[j+gap]=li[j] 11 j=j-gap 12 li[j+gap]=tmp 13 gap=int(gap/2) 14 15 data=list(range(100)) 16 random.shuffle(data) 17 print(data) 18 shell_sort(data) 19 print(data)
3.8其它排序-基数排序
简单了解 略过！
3.9总结
各种排序的稳定性，时间复杂度和空间复杂度总结：
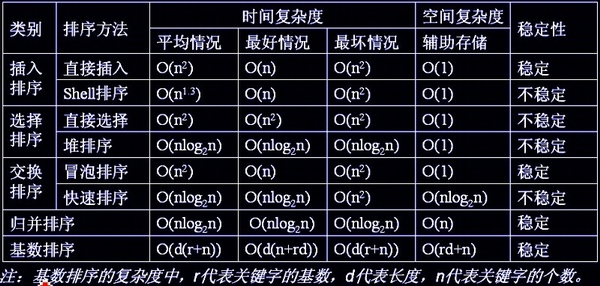
我们比较时间复杂度函数的情况：
时间复杂度函数O(n)的增长情况
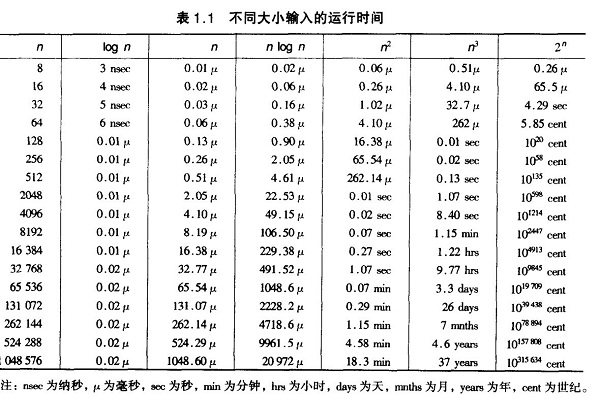
所以对n较大的排序记录。一般的选择都是时间复杂度为O(nlog2n)的排序方法。
时间复杂度来说：
(1)平方阶(O(n2))排序
各类简单排序:插入、选择和冒泡排序；
时间复杂度：O(n2)
空间复杂度：O(1)
(2)线性对数阶(O(nlog2n))排序
快速排序、堆排序和归并排序；
三种排序算法的时间复杂度都是O(nlog2n)
一般情况下，就运行时间而言：
快速排序 < 归并排序 < 堆排序
三种排序算法的缺点：
快速排序：极端情况下排序效率低
归并排序：需要额外的内存开销
堆排序：在快的排序算法中相对较
(3)O(n1+§))排序,§是介于0和1之间的常数。
希尔排序
(4)线性阶(O(n))排序
基数排序
说明：
当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O（n）；
而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O（n2）；
原表是否有序，对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
稳定性：
排序算法的稳定性:若待排序的序列中，存在多个具有相同关键字的记录，经过排序， 这些记录的相对次序保持不变，则称该算法是稳定的；若经排序后，记录的相对 次序发生了改变，则称该算法是不稳定的。
稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。另外，如果排序算法稳定，可以避免多余的比较；
稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序
不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序
选择排序算法准则：
每种排序算法都各有优缺点。因此，在实用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。
选择排序算法的依据
影响排序的因素有很多，平均时间复杂度低的算法并不一定就是最优的。相反，有时平均时间复杂度高的算法可能更适合某些特殊情况。同时，选择算法时还得考虑它的可读性，以利于软件的维护。一般而言，需要考虑的因素有以下四点：
1．待排序的记录数目n的大小；
2．记录本身数据量的大小，也就是记录中除关键字外的其他信息量的大小；
3．关键字的结构及其分布情况；
4．对排序稳定性的要求。
设待排序元素的个数为n.
1）当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。
快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
堆排序 ： 如果内存空间允许且要求稳定性的，
归并排序：它有一定数量的数据移动，所以我们可能过与插入排序组合，先获得一定长度的序列，然后再合并，在效率上将有所提高。
2） 当n较大，内存空间允许，且要求稳定性 =》归并排序
3）当n较小，可采用直接插入或直接选择排序。
直接插入排序：当元素分布有序，直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序 ：元素分布有序，如果不要求稳定性，选择直接选择排序
5）一般不使用或不直接使用传统的冒泡排序。
6）基数排序
它是一种稳定的排序算法，但有一定的局限性：
1、关键字可分解。
2、记录的关键字位数较少，如果密集更好
3、如果是数字时，最好是无符号的，否则将增加相应的映射复杂度，可先将其正负分开排序。
3.10排序算法的应用
3.10.1计数排序
现在有一个列表，列表中的数范围都在0到100之间，列表长度大约为100万。设计算法在O(n)时间复杂度内将列表进行排序。
1 #Author:ajun 2 import random 3 def count_sort(li, max_num): 4 count = [0 for i in range(max_num + 1)] 5 for num in li: 6 count[num] += 1 7 i = 0 8 for num,m in enumerate(count): 9 for j in range(m): 10 li[i] = num 11 i += 1 12 13 data=[] 14 for i in range(1000): 15 data.append(random.randint(0,100)) 16 random.shuffle(data) 17 print(data) 18 count_sort(data,100) 19 print(data)
通过申请100个空间，通过空间计数，从而节约时间。
1 import random 2 import time 3 import copy 4 import sys 5 def cal_time(func): 6 def wrapper(*args, **kwargs): 7 t1 = time.time() 8 result = func(*args, **kwargs) 9 t2 = time.time() 10 print("%s running time: %s secs." % (func.__name__, t2 - t1)) 11 return result 12 return wrapper 13 @cal_time 14 def bubble_sort(li): 15 for i in range(len(li) - 1): 16 for j in range(len(li) - i - 1): 17 if li[j] > li[j+1]: 18 li[j], li[j+1] = li[j+1], li[j] 19 @cal_time 20 def bubble_sort_1(li): 21 for i in range(len(li) - 1): 22 exchange = False 23 for j in range(len(li) - i - 1): 24 if li[j] > li[j+1]: 25 li[j], li[j+1] = li[j+1], li[j] 26 exchange = True 27 if not exchange: 28 break 29 def select_sort(li): 30 for i in range(len(li) - 1): 31 min_loc = i 32 for j in range(i+1,len(li)): 33 if li[j] < li[min_loc]: 34 min_loc = j 35 li[i], li[min_loc] = li[min_loc], li[i] 36 def insert_sort(li): 37 for i in range(1, len(li)): 38 tmp = li[i] 39 j = i - 1 40 while j >= 0 and li[j] > tmp: 41 li[j+1]=li[j] 42 j = j - 1 43 li[j + 1] = tmp 44 def quick_sort_x(data, left, right): 45 if left < right: 46 mid = partition(data, left, right) 47 quick_sort_x(data, left, mid - 1) 48 quick_sort_x(data, mid + 1, right) 49 50 def partition(data, left, right): 51 tmp = data[left] 52 while left < right: 53 while left < right and data[right] >= tmp: 54 right -= 1 55 data[left] = data[right] 56 while left < right and data[left] <= tmp: 57 left += 1 58 data[right] = data[left] 59 data[left] = tmp 60 return left 61 @cal_time 62 def quick_sort(data): 63 return quick_sort_x(data, 0, len(data) - 1) 64 @cal_time 65 def sys_sort(data): 66 return data.sort() 67 def sift(data, low, high): 68 i = low 69 j = 2 * i + 1 70 tmp = data[i] 71 while j <= high: #孩子在堆里 72 if j + 1 <= high and data[j] < data[j+1]: #如果有右孩子且比左孩子大 73 j += 1 #j指向右孩子 74 if data[j] > tmp: #孩子比最高领导大 75 data[i] = data[j] #孩子填到父亲的空位上 76 i = j #孩子成为新父亲 77 j = 2 * i +1 #新孩子 78 else: 79 break 80 data[i] = tmp #最高领导放到父亲位置 81 @cal_time 82 def heap_sort(data): 83 n = len(data) 84 for i in range(n // 2 - 1, -1, -1): 85 sift(data, i, n - 1) 86 #堆建好了 87 for i in range(n-1, -1, -1): #i指向堆的最后 88 data[0], data[i] = data[i], data[0] #领导退休，刁民上位 89 sift(data, 0, i - 1) #调整出新领导 90 91 def merge(li, low, mid, high): 92 i = low 93 j = mid + 1 94 ltmp = [] 95 while i <= mid and j <= high: 96 if li[i] < li[j]: 97 ltmp.append(li[i]) 98 i += 1 99 else: 100 ltmp.append(li[j]) 101 j += 1 102 while i <= mid: 103 ltmp.append(li[i]) 104 i += 1 105 while j <= high: 106 ltmp.append(li[j]) 107 j += 1 108 li[low:high+1] = ltmp 109 110 def _mergesort(li, low, high): 111 if low < high: 112 mid = (low + high) // 2 113 _mergesort(li,low, mid) 114 _mergesort(li, mid+1, high) 115 merge(li, low, mid, high) 116 117 @cal_time 118 def mergesort(li): 119 _mergesort(li, 0, len(li) - 1) 120 121 @cal_time 122 123 def insert_sort(li): 124 for i in range(1,len(li)): 125 tmp=li[i] 126 j=i-1 127 while j >= 0 and li[j] > tmp: 128 li[j+1]=li[j] 129 j=j-1 130 li[j+1]=tmp 131 @cal_time 132 def shell_sort(li): 133 gap = int(len(li) // 2) 134 while gap >= 1: 135 for i in range(gap, len(li)): 136 li[j+1]=li[j] 137 j = j - 1 138 tmp = li[i] 139 j = i - gap 140 while j >= 0 and tmp < li[j]: 141 li[j + gap] = li[j] 142 j -= gap 143 li[i - gap] = tmp 144 gap = gap // 2 145 146 147 @cal_time 148 def count_sort(li, max_num): 149 count = [0 for i in range(max_num + 1)] 150 for num in li: 151 count[num] += 1 152 i = 0 153 for num,m in enumerate(count): 154 for j in range(m): 155 li[i] = num 156 i += 1 157 158 @cal_time 159 def insert_sort(li): 160 for i in range(1, len(li)): 161 tmp = li[i] 162 j = i - 1 163 while j >= 0 and li[j] > tmp: 164 li[j+1]=li[j] 165 j = j - 1 166 li[j + 1] = tmp 167 168 def topn(li, n): 169 heap = li[0:n] 170 for i in range(n // 2 - 1, -1, -1): 171 sift(heap, i, n - 1) 172 #遍历 173 for i in range(n, len(li)): 174 if li[i] > heap[0]: 175 heap[0] = li[i] 176 sift(heap, 0, n - 1) 177 for i in range(n - 1, -1, -1): # i指向堆的最后 178 heap[0], heap[i] = heap[i], heap[0] # 领导退休，刁民上位 179 sift(heap, 0, i - 1) # 调整出新领导 180 return heap 181 182 data_data = [] 183 sys.setrecursionlimit(100000)#增加递归的层数 184 for i in range(100000): 185 data_data.append(random.randint(0,100)) 186 # # data.sort() 187 random.shuffle(data_data) 188 data1 = copy.deepcopy(data_data) 189 data2 = copy.deepcopy(data_data) 190 data3 = copy.deepcopy(data_data) 191 data4 = copy.deepcopy(data_data) 192 # # 193 #bubble_sort(data3) 194 quick_sort(data2) 195 count_sort(data1, 100) 196 sys_sort(data4)
结果
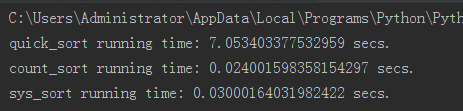
通过比较发现，快速排序用了7秒，计数排序用了0.02秒，系统的自带的（一般用C实现的排序），用了0.03秒。
3.10.2 TOP10--海量数据取最大的十个数。
现在有n个数（n>10000），设计算法，按大小顺序得到前10大的数。
1 import random 2 3 def insert(li, i): 4 tmp = li[i] 5 j = i - 1 6 while j >= 0 and li[j] > tmp: 7 li[j + 1] = li[j] 8 j = j - 1 9 li[j + 1] = tmp 10 11 def insert_sort(li): 12 for i in range(1, len(li)): 13 insert(li, i) 14 15 16 def topk(li, k): 17 top = li[0:k + 1] 18 insert_sort(top) 19 for i in range(k+1, len(li)): 20 top[k] = li[i] 21 insert(top, k) 22 return top[:-1] 23 24 25 def sift(data, low, high): 26 i = low 27 j = 2 * i + 1 28 tmp = data[i] 29 while j <= high: #孩子在堆里 30 if j + 1 <= high and data[j] < data[j+1]: #如果有右孩子且比左孩子大 31 j += 1 #j指向右孩子 32 if data[j] > tmp: #孩子比最高领导大 33 data[i] = data[j] #孩子填到父亲的空位上 34 i = j #孩子成为新父亲 35 j = 2 * i +1 #新孩子 36 else: 37 break 38 data[i] = tmp #最高领导放到父亲位置 39 40 def topn(li, n): 41 heap = li[0:n] 42 for i in range(n // 2 - 1, -1, -1): 43 sift(heap, i, n - 1) 44 #遍历 45 for i in range(n, len(li)): 46 if li[i] < heap[0]: 47 heap[0] = li[i] 48 sift(heap, 0, n - 1) 49 for i in range(n - 1, -1, -1): # i指向堆的最后 50 heap[0], heap[i] = heap[i], heap[0] # 领导退休，刁民上位 51 sift(heap, 0, i - 1) # 调整出新领导 52 return heap 53 54 data = list(range(10000)) 55 random.shuffle(data) 56 print(topn(data, 10)) 57 #print(topk(data, 10))
思路：
1）topk方法就是插入排序。插入排序法：先将前10个排序作为初步结果，然后对剩余990个进行循环，每个值与结果t中的值比较，如果比里面的某个值大，那么删掉里面最小的。保持只有10个值。等循环完毕，那么最终结果TOP10。
2）topn方法就是堆排序思路，解决这类问题的最佳思路。
取列表前10个元素建立一个小根堆。堆顶就是目前第10大的数。
依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整；
遍历列表所有元素后，倒序弹出堆顶。
3.10.3练习题
1）给定一个列表和一个整数，设计算法找到两个数的下标，使得两个数之和为给定的整数。保证肯定仅有一个结果。例如，列表[1,2,5,4]与目标整数3，1+2=3，结果为(0, 1).
1 import copy 2 li = [1, 5, 4, 2] 3 target = 3 4 max_num = 100 5 6 def func1(): 7 for i in range(len(li)): 8 for j in range(i+1, len(li)): 9 if li[i] + li[j] == target: 10 return (i,j) 11 12 def bin_search(data_set, val, low, high): 13 while low <= high: 14 mid = (low+high)//2 15 if data_set[mid] == val: 16 return mid 17 elif data_set[mid] < val: 18 low = mid + 1 19 else: 20 high = mid - 1 21 return 22 23 def func2(): 24 li2 = copy.deepcopy(li) 25 li2.sort() 26 for i in range(len(li2)): 27 a = i 28 b = bin_search(li2, target - li2[a], i+1, len(li2)-1) 29 if b: 30 return (li.index(li2[a]),li.index(li2[b])) 31 32 def func3(): 33 a = [None for i in range(max_num+1)] 34 for i in range(len(li)): 35 a[li[i]] = i 36 if a[target-li[i]] != None: 37 return (a[li[i]], a[target-li[i]]) 38 39 40 print(func1())
三种思路
（1）：穷举法，全部测试。
（2）：通过二分查找的思路
（3）：时间复杂度最少，通过列表的查找。
2）给定一个升序列表和一个整数，返回该整数在列表中的下标范围。例如：列表[1,2,3,3,3,4,4,5]，若查找3，则返回(2,4)；若查找1，则返回(0,0)。
1 def bin_search(data_set, val): 2 low = 0 3 high = len(data_set) - 1 4 while low <= high: 5 mid = (low+high)//2 6 if data_set[mid] == val: 7 left = mid 8 right = mid 9 while left >= 0 and data_set[left] == val: 10 left -= 1 11 while right < len(data_set) and data_set[right] == val: 12 right += 1 13 return (left + 1, right - 1) 14 elif data_set[mid] < val: 15 low = mid + 1 16 else: 17 high = mid - 1 18 return (-1, -1) 19 20 21 def bin_search(data_set, val): 22 low = 0 23 high = len(data_set) - 1 24 while low <= high: 25 mid = (low+high)//2 26 if data_set[mid] == val: 27 left = mid 28 right = mid 29 while left >= 0 and data_set[left] == val: 30 left -= 1 31 while right < len(data_set) and data_set[right] == val: 32 right += 1 33 return (left + 1, right - 1) 34 elif data_set[mid] < val: 35 low = mid + 1 36 else: 37 high = mid - 1 38 return 39 40 41 42 li = [1,2,3,3,3,4,4,5] 43 print(bin_search(li, 3))
四、简单数据结构
数据结构就是设计数据以何种方式组织并存储在计算机中。
比如：列表、集合与字典等都是一种数据结构。 “程序=数据结构+算法”
Python中特有的-----列表：在其他编程语言中称为“数组”，是一种基本的数据结构类型。
关于列表的问题：
列表中元素使如何存储的？
列表提供了哪些基本的操作？
这些操作的时间复杂度是多少？
4.1栈
4.1 栈的定义
栈(Stack)是一个数据集合，可以理解为只能在一端进行插入或删除操作的列表。栈的特点：后进先出（last-in, first-out）。如下所示：
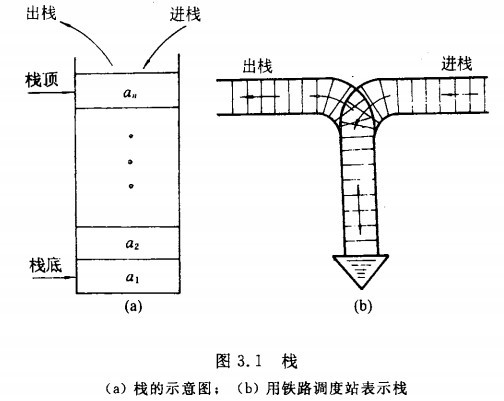
栈的基本运算有六种：
构造空栈：创建列表、
判栈空: 判断列表是否为空、
判栈满：
进栈：可形象地理解为压入，这时栈中会多一个元素
退栈： 可形象地理解为弹出，弹出后栈中就无此元素了。
取栈顶元素：不同与弹出，只是使用栈顶元素的值，该元素仍在栈顶不会改变。
对于Python来说，栈用列表实现的。栈的操作一般只有三种，出栈（pop），进栈（append），查看栈顶元素（[-1]）。
栈的应用：
1）括号匹配问题：给一个字符串，其中包含小括号、中括号、大括号，求该字符串中的括号是否匹配。
例如：()()[]{} 匹配 ([{()}]) 匹配
[]( 不匹配 [(]) 不匹配
1 def cheak_kuohao(s): 2 stack = [] 3 for char in s: 4 if char in {'(','[', '{'}: 5 stack.append(char) 6 elif char == ')': 7 if len(stack)>0 and stack[-1]=='(': 8 stack.pop() 9 else: 10 return False 11 elif char == ']': 12 if len(stack) > 0 and stack[-1] == '[': 13 stack.pop() 14 else: 15 return False 16 elif char == '}': 17 if len(stack)>0 and stack[-1]=='{': 18 stack.pop() 19 else: 20 return False 21 if len(stack) == 0: 22 return True 23 else: 24 return False 25 26 27 print(cheak_kuohao('()[]{{[]}}'))
2）迷宫问题
给一个二维列表，表示迷宫（0表示通道，1表示围墙）。给出算法，求一条走出迷宫的路径。
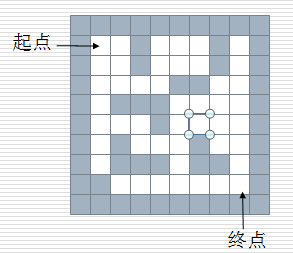
maze = [
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
1 maze = [ 2 [1,1,1,1,1,1,1,1,1,1], 3 [1,0,0,1,0,0,0,1,0,1], 4 [1,0,0,1,0,0,0,1,0,1], 5 [1,0,0,0,0,1,1,0,0,1], 6 [1,0,1,1,1,0,0,0,0,1], 7 [1,0,0,0,1,0,0,0,0,1], 8 [1,0,1,0,0,0,1,0,0,1], 9 [1,0,1,1,1,0,1,1,0,1], 10 [1,1,0,0,0,0,0,1,0,1], 11 [1,1,1,1,1,1,1,1,1,1] 12 ] 13 14 dirs = [lambda x, y: (x + 1, y), 15 lambda x, y: (x - 1, y), 16 lambda x, y: (x, y - 1), 17 lambda x, y: (x, y + 1)] 18 19 def mpath(x1, y1, x2, y2): 20 stack = [] 21 stack.append((x1, y1)) 22 while len(stack) > 0: 23 curNode = stack[-1] 24 if curNode[0] == x2 and curNode[1] == y2: 25 #到达终点 26 for p in stack: 27 print(p) 28 return True 29 for dir in dirs: 30 nextNode = dir(curNode[0], curNode[1]) 31 if maze[nextNode[0]][nextNode[1]] == 0: 32 #找到了下一个 33 stack.append(nextNode) 34 maze[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过，防止死循环 35 break 36 else:#四个方向都没找到 37 maze[curNode[0]][curNode[1]] = -1 # 死路一条,下次别走了 38 stack.pop() #回溯 39 print("没有路") 40 return False 41 42 mpath(1,1,8,8)
3）汉诺塔的问题：
解决：
1）如果有一个盘子，直接从X移到Z即可。
2）如果有n个盘子要从X移到Z，Y作为辅助。问题可以转化为，先将上面n-1个从X移动到Y，Z作为辅助，然后将第n个从X移动到Z，最后将剩余的n-1个从Y移动到Z，X作为辅助。
4.2队列
Queue是一种先进先出的数据结构，和Stack一样，他也有链表和数组两种实现，理解了Stack的实现后，Queue的实现就比较简单了。
队列(Queue)是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。
进行插入的一端称为队尾(rear)，插入动作称为进队或入队
进行删除的一端称为队头(front)，删除动作称为出队
队列的性质：先进先出(First-in, First-out)
双向队列：队列的两端都允许进行进队和出队操作。
队列能否简单用列表实现？为什么？
使用方法：from collections import deque
创建队列：queue = deque(li)
进队：append
出队：popleft
双向队列队首进队：appendleft
双向队列队尾进队：pop
队列的实现原理:
初步设想：列表+两个下标指针
创建一个列表和两个变量，front变量指向队首，rear变量指向队尾。初始时，front和rear都为0。
进队操作：元素写到li[rear]的位置，rear自增1。
出队操作：返回li[front]的元素，front自减1。
这种实现的问题？
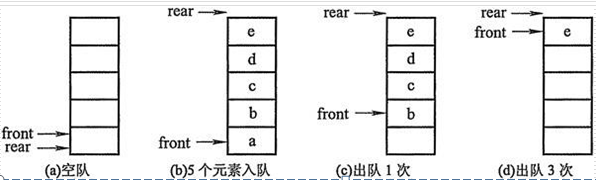
队列的实现原理——环形队列
改进方案：将列表首尾逻辑上连接起来。
环形队列：当队尾指针front == Maxsize + 1时，再前进一个位置就自动到0。
实现方式：求余数运算
队首指针前进1：front = (front + 1) % MaxSize
队尾指针前进1：rear = (rear + 1) % MaxSize
队空条件：rear == front
队满条件：(rear + 1) % MaxSize == front
1 from collections import deque 2 3 queue = deque() 4 queue.append(1) 5 queue.append(2) 6 print(queue.popleft())
队列的应用：
1）迷宫问题
在解栈的迷宫问题，使用队列的方法：
1 from collections import deque 2 3 mg = [ 4 [1,1,1,1,1,1,1,1,1,1], 5 [1,0,0,1,0,0,0,1,0,1], 6 [1,0,0,1,0,0,0,1,0,1], 7 [1,0,0,0,0,1,1,0,0,1], 8 [1,0,1,1,1,0,0,0,0,1], 9 [1,0,0,0,1,0,0,0,0,1], 10 [1,0,1,0,0,0,1,0,0,1], 11 [1,0,1,1,1,0,1,1,0,1], 12 [1,1,0,0,0,0,0,1,0,1], 13 [1,1,1,1,1,1,1,1,1,1] 14 ] 15 16 dirs = [lambda x, y: (x + 1, y), 17 lambda x, y: (x - 1, y), 18 lambda x, y: (x, y - 1), 19 lambda x, y: (x, y + 1)] 20 21 def print_p(path): 22 curNode = path[-1] 23 realpath = [] 24 print('迷宫路径为：') 25 while curNode[2] != -1: 26 realpath.append(curNode[0:2]) 27 curNode = path[curNode[2]] 28 realpath.append(curNode[0:2]) 29 realpath.reverse() 30 print(realpath) 31 32 def mgpath(x1, y1, x2, y2): 33 queue = deque() 34 path = [] 35 queue.append((x1, y1, -1)) 36 while len(queue) > 0: 37 curNode = queue.popleft() 38 path.append(curNode) 39 if curNode[0] == x2 and curNode[1] == y2: 40 #到达终点 41 print_p(path) 42 return True 43 for dir in dirs: 44 nextNode = dir(curNode[0], curNode[1]) 45 if mg[nextNode[0]][nextNode[1]] == 0: # 找到下一个方块 46 queue.append((*nextNode, len(path) - 1)) 47 mg[nextNode[0]][nextNode[1]] = -1 # 标记为已经走过 48 return False 49 50 51 mgpath(1,1,8,8)
2）银行排队
3）模拟打印机缓冲区。
在主机将数据输出到打印机时，会出现主机速度与打印机的打印速度不匹配的问题。这时主机就要停下来等待打印机。显然，这样会降低主机的使用效率。为此人们设想了一种办法：为打印机设置一个打印数据缓冲区，当主机需要打印数据时，先将数据依次写入这个缓冲区，写满后主机转去做其他的事情，而打印机就从缓冲区中按照先进先出的原则依次读取数据并打印，这样做即保证了打印数据的正确性，又提高了主机的使用效率。由此可见，打印机缓冲区实际上就是一个队列结构。
4）CPU分时系统
在一个带有多个终端的计算机系统中，同时有多个用户需要使用CPU运行各自的应用程序，它们分别通过各自的终端向操作系统提出使用CPU的请求，操作系统通常按照每个请求在时间上的先后顺序，将它们排成一个队列，每次把CPU分配给当前队首的请求用户，即将该用户的应用程序投入运行，当该程序运行完毕或用完规定的时间片后，操作系统再将CPU分配给新的队首请求用户，这样即可以满足每个用户的请求，又可以使CPU正常工作。
4.3链表
链表中每一个元素都是一个对象，每个对象称为一个节点，包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接，最终串联成一个链表。
节点的定义：
class Node(object):
def __init__(self, item):
self.item = item
self.next = None
头结点：
遍历链表：
def traversal(head):
curNode = head # 临时用指针
while curNode is not None:
print(curNode.data)
curNode = curNode.next
插入：
p.next = curNode.next
curNode.next = p
删除：
p = curNode.next
curNode.next = curNode.next.next
del p
头插法：
def createLinkListF(li):
l = Node()
for num in li:
s = Node(num)
s.next = l.next
l.next = s
return l
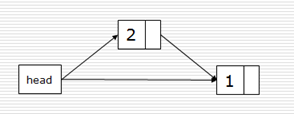
尾插法：
def createLinkListR(li):
l = Node()
r = l #r指向尾节点
for num in li:
s = Node(num)
r.next = s
r = s
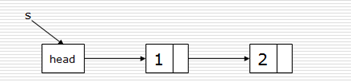
单链表的基本操作：
1 class Node(object): 2 def __init__(self, item=None): 3 self.item = item 4 self.next = None 5 6 head = Node() 7 head.next = Node(20) 8 head.next.next = Node(30) 9 10 def traversal(head): 11 curNode = head # 临时用指针 12 while curNode is not None: 13 print(curNode.item) 14 curNode = curNode.next 15 16 traversal(head)
双链表：
- 双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。
- 节点定义：
节点的定义：
class Node(object):
def __init__(self, item=None):
self.item = item
self.next = None
self.prior = None
双链表的插入：
p.next = curNode.next
curNode.next.prior = p
p.prior = curNode
curNode.next = p
双链表的删除：
p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p
建立双链表：
尾插法：
def createLinkListR(li):
l = Node()
r = l
fornum inli:
s = Node(num)
r.next = s
s.prior = r
r = s
returnl, r
列表与链表
1）按元素值查找
2）按下标查找
3）在某元素后插入
4）删除某元素
4.4哈希查找
哈希值是一段由其他某个值(标识) 映射 成为的一段占用更小的内存更少的数据空间的值。
而哈希表是 根据 指定的某个hash函数H(key)，和处理冲突的方法，将一组关键字映射到另一个有限的区间上，映射得到的值（根据算法和解决冲突方法得到） 就可以作为记录在哈希表中的存放的具体位置。
哈希查找是通过计算数据元素的存储地址进行查找的一种方法。
比如”5“是一个要保存的数，然后我丢给哈希函数，哈希函数给我返回一个”2”，那么此时的”5“和“2”就建立一种对应关系，这种关系就是所谓的“哈希关系”，在实际应用中也就形成了”2“是key，”5“是value。
哈希必须要遵守两点原则：
①: key尽可能的分散，也就是我丢一个“6”和“5”给你，你都返回一个“2”，那么这样的哈希函数不尽完美。
②： 哈希函数尽可能的简单，也就是说丢一个“6”给你，你哈希函数要搞1小时才能给我，这样也是不好的。
常用的哈希函数构造方法：
- 直接定址法：很容易理解，key=Value+C； 这个“C”是常量。Value+C其实就是一个简单的哈希函数。
- 除法取余法： 很容易理解， key=value%C;解释同上。
- 数字分析法：这种蛮有意思，比如有一组value1=112233，value2=112633，value3=119033，针对这样的数我们分析数中间两个数比较波动，其他数不变。那么我们取key的值就可以是key1=22,key2=26,key3=90。
- 平方取中法。此处忽略，见名识意。
-
折叠法：这种蛮有意思,比如value=135790，要求key是2位数的散列值。那么我们将value变为13+57+90=160，然后去掉高位“1”,此时key=60，哈哈，这就是他们的哈希关系，这样做的目的就是key与每一位value都相关，来做到“散列地址”尽可能分散的目地。·
当两个不同的数据元素的哈希值相同时，就会发生冲突。解决冲突常用的手法有2种：
- 开放地址法：如果两个数据元素的哈希值相同，则在哈希表中为后插入的数据元素另外选择一个表项。当程序查找哈希表时，如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素，程序就会继续往后查找，直到找到一个符合查找要求的数据元素，或者遇到一个空的表项。
- 链接法：将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。
同样的长度，把标识的数据项给压缩了，并且加上冲突处理方法，那就是另 外一串查找起来相当简单同时不会出错的线性表，而且我们是省略了一大堆无用的查找，首先直接找到有可能正确的数据项来比较，那就说明正确的那个项一定就在我们起始找的那个元素的附近，或者就是它，这不就是我们想要的吗？
哈希这种映射的方法将查找数的时间复杂度变成了一个算法常数，无论你查找什么数，先执行指定的hash算法，之后按照解决冲突的方法去查找，这个效率比起线性表和队列这些同为线性数据结构的家伙，那可是快了不只一点点。
1 #Author:ajun 2 3 #除法取余法实现的哈希函数 4 def myHash(data,hashLength,): 5 return data % hashLength 6 #哈希表检索数据 7 def searchHash(hash,hashLength,data): 8 hashAddress=myHash(data,hashLength) 9 #指定hashAddress存在，但并非关键值，则用开放寻址法解决 10 while hash.get(hashAddress) and hash[hashAddress]!=data: 11 hashAddress+=1 12 hashAddress=hashAddress%hashLength 13 if hash.get(hashAddress)==None: 14 return None 15 return hashAddress 16 17 #数据插入哈希表 18 def insertHash(hash,hashLength,data): 19 hashAddress=myHash(data,hashLength) 20 #如果key存在说明应经被别人占用， 需要解决冲突 21 while(hash.get(hashAddress)): 22 #用开放寻执法 23 hashAddress+=1 24 hashAddress=myHash(data,hashLength) 25 hash[hashAddress]=data 26 27 if __name__ == '__main__': 28 hashLength=20 29 L=[13, 29, 27, 28, 26, 30, 38 ] 30 hash={} 31 for i in L: 32 insertHash(hash,hashLength,i) 33 result=searchHash(hash,hashLength,22) 34 if result: 35 print("数据已找到，索引位置在",result) 36 print(hash[result]) 37 else: 38 print("没有找到数据")
hash还广泛应用于加密和数据校验中，hash的128位加密具有不可逆性，像MD5，咱们通常用的WAP/WAP2协议也是应用到了hash技术