《MLR——基于attention的LR》

MLR——基于attention的LR

 

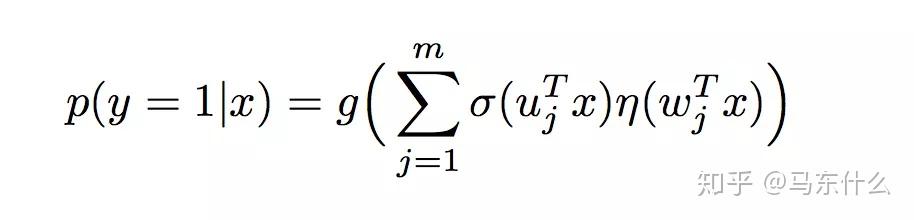
MLR的表达式，其中g(x)=x,u是聚类参数，决定了空间的划分，w是分类参数，决定空间内的预测。这里面超参数分片数m可以较好地平衡模型的拟合与推广能力。

MLR的初衷设计是非常直观的，以风控为例，假设我们有一批坏用户，这些坏用户都是预期超过某个期限被系统判定为坏客户的人，其中可能有一部分是专业的欺诈分子（不还钱），有一部分是忘记还款，有一部分是职业老赖（可能还，但是周期长），这些用户的特征分布可能是不同的，例如像这样：

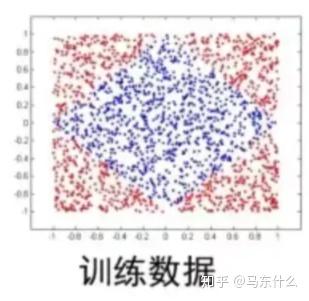
显然四个角的用户的特征情况不同，如果单纯使用lr无法拟合这种非线性的分类边界，

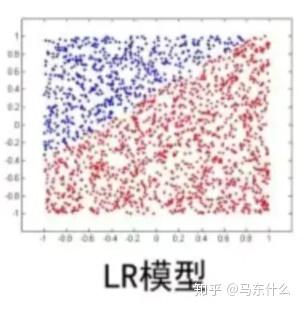
这个时候，使用mlr就可以实现很好的拟合效果，

在实际中，MLR算法常用的形式如下，使用softmax作为分片函数：

实际上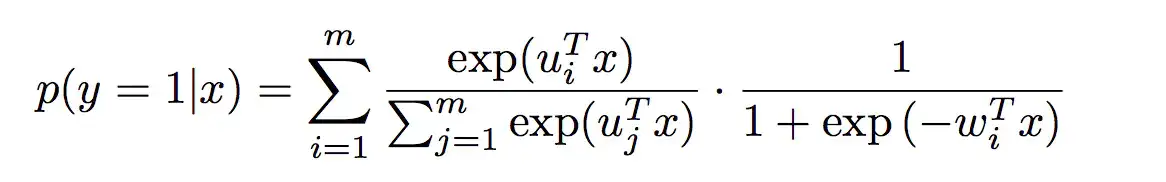

上式如果m=1，就退化成了普通的逻辑回归的形式，这是一个很有意思的地方，假设空间存在非线性的分界面难以直接使用线性模型来拟合分界面，那么我们就使用多个带权重的线性模型来拟合非线性的分界面，类似这样：

假设我们的分界面是这样的，用单个线性模型无法拟合，但是通过多个线性模型的叠加就可以拟合出来了。实际上就是带权的多个lr的叠加，只不过这里的权重系数不是人为定义而是模型学出来的。

下面看看tf的代码实现，可惜没找到keras的，否则会更好理解：

from：

https://github.com/princewen/tensorflow_practice/tree/master/recommendation/Basic-MLR-Demo​github.com

import tensorflow as tf
import time
from sklearn.metrics import roc_auc_score
from data import get_data
import pandas as pd


x = tf.placeholder(tf.float32,shape=[None,108])
y = tf.placeholder(tf.float32,shape=[None])


m = 2
learning_rate = 0.3
u = tf.Variable(tf.random_normal([108,m],0.0,0.5),name='u')
w = tf.Variable(tf.random_normal([108,m],0.0,0.5),name='w')

U = tf.matmul(x,u)
p1 = tf.nn.softmax(U)

W = tf.matmul(x,w)
p2 = tf.nn.sigmoid(W)

pred = tf.reduce_sum(tf.multiply(p1,p2),1)

cost1=tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=pred, labels=y))
cost=tf.add_n([cost1])
train_op = tf.train.FtrlOptimizer(learning_rate).minimize(cost)
train_x,train_y,test_x,test_y = get_data()
time_s=time.time()
result = []
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(0, 10000):
        f_dict = {x: train_x, y: train_y}

        _, cost_, predict_ = sess.run([train_op, cost, pred], feed_dict=f_dict)

        auc = roc_auc_score(train_y, predict_)
        time_t = time.time()
        if epoch % 100 == 0:
            f_dict = {x: test_x, y: test_y}
            _, cost_, predict_test = sess.run([train_op, cost, pred], feed_dict=f_dict)
            test_auc = roc_auc_score(test_y, predict_test)
            print("%d %ld cost:%f,train_auc:%f,test_auc:%f" % (epoch, (time_t - time_s), cost_, auc, test_auc))
            result.append([epoch,(time_t - time_s),auc,test_auc])

pd.DataFrame(result,columns=['epoch','time','train_auc','test_auc']).to_csv("data/mlr_"+str(m)+'.csv')

为什么说MLR是引入了注意力机制的LR，重点看这里：（原始输入数据维度108，要注意）

u = tf.Variable(tf.random_normal([108,m],0.0,0.5),name='u')
w = tf.Variable(tf.random_normal([108,m],0.0,0.5),name='w')

U = tf.matmul(x,u)
p1 = tf.nn.softmax(U)

W = tf.matmul(x,w)
p2 = tf.nn.sigmoid(W)

pred = tf.reduce_sum(tf.multiply(p1,p2),1)

相对于 所谓的 q v k，我觉得从 “加权求和”的角度来理解attention 机制会更加直观自然，对于结构化数据来说，包括后面的AFM，实际上从加权求和的角度来理解attention要简单的多，并且在实现上也是基于这样的思路来进行非常easy的搭建的,说老实话我也不知道怎么从 q v k的角度来解释这种基于结构化数据的attention机制。

MLR的输入层是样本的特征向量，中间层是一个有m个神经元的隐层，然后输入层是一个单神经元的隐层带sigmoid，去掉中间的隐层就是一个普通的逻辑回归的结构。所以注意力机制体现在这里的m神经元隐层和输出层之间，前面说过，m是分片数，也就是假设用多少个线性分界面去拟合非线性分界面：

U = tf.matmul(x,u)
p1 = tf.nn.softmax(U)

这里我们对x和u相乘得到一个m*1的矩阵，【score1，score2.。。。score m】，从mlr的公式角度来说，score代表的就是当前输入x对应到m个分片的概率值，这里的attention就体现在，以上图为例，假设我们的输入x是在深蓝色的那条分界线对应的分片，显然此时我们希望这个分片对应的那个lr的权重系数尽量大，而其他分片的lr对应的权重尽量小，依此类推。

然后就有了：

W = tf.matmul(x,w)
p2 = tf.nn.sigmoid(W)

pred = tf.reduce_sum(tf.multiply(p1,p2),1)

然后对m个逻辑回归进行加权再reduce sum求和，完成了整个mlr的前向传播的流程的定义。

 

这么做的好处是什么呢，举一个极端的例子，假设我们的注意力机制使得此时深蓝色lr对应的分片概率为1，其它分片概率为0，此时模型进行反向传播的过程中，梯度仅仅在深蓝色分片对应的lr上进行传播，即模型将全部的注意力都集中在与当前任务最相关的分片lr的权重系数的更新上而不会对其他无关的分片的lr的权重系数进行更新。这样在一定程度上“可能”能够有效的减少迭代的次数从而更加迅速的完成收敛。并且其余不相关的分片上的样本对于其它分片上的lr的训练的影响大大降低（试想一下，如果没有引入attention，则所有的样本都会用于更新唯一的一个分片，使得模型在训练的过程中发生了很多无效的更新）。

 

总而言之，通过引入attention机制，我们可以根据我们的输入x来有选择有侧重的更新我们的W矩阵，从而提高模型的训练效率和泛化性能。（B分片的样本对A分片的分界面的权重系数带来的影响其实类似于引入噪声，印象模型的泛化性能）。

发布于 2020-04-13