ICML 2020|华为诺亚方舟8篇论文入选,多智能体强化学习成热点
华为诺亚方舟实验室此次有8篇论文被接收,创下ICML历届论文接收量新高。研究方向涵盖多智能体强化学习,神经网络架构搜索,1bit神经网络,图结构数据上的主动学习,记忆增强学习,理论样本复杂度分析。下面我们就来看下本次接收的几篇代表性论文。
Training Binary Neural Networks through Learning with Noisy Supervision
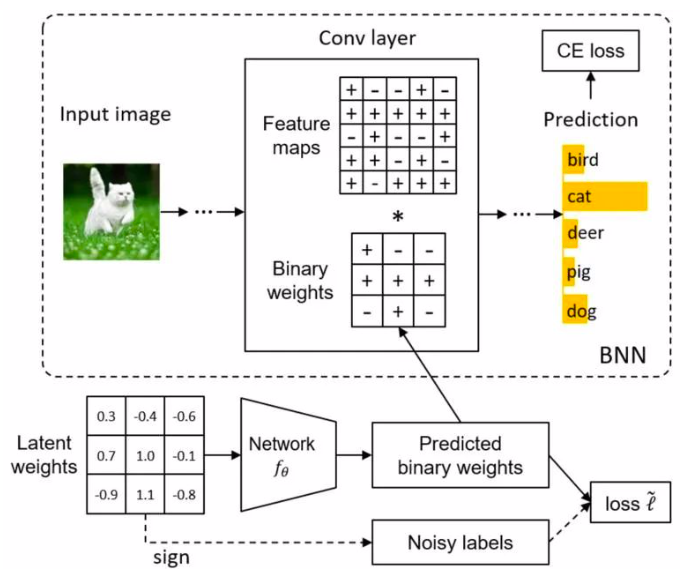
本文从学习的角度对二值神经网络上的二值化运算进行研究。与经典的手工规则(例如Sign函数)将神经元二值化相比,我们提出映射模型(Mapping model)来学习从全精度神经元到二值神经元的映射。这里,每个权值不是独立二值化,而是将权值张量作为一个整体来完成二值化,充分考虑权值之间的关联性。
为了帮助训练二值化映射模型,我们将传统Sign函数量化的神经元视为一些辅助监督信号,其虽然有噪声但仍具有指导意义。因此,我们引入了无偏估计器以减轻噪声的影响。在基准数据集上的实验结果表明,所提出的二值化技术具有广泛的有效性。
多智能体深度强化学习下的Q值路径分解
许多现实世界中的复杂场景可以建模为多智能体系统,因此多智能体深度强化学习(MARL)作为一种重要的分布式优化技术,已成为一个非常活跃的研究领域。
其中一类重要且普遍的场景为部分可观察的合作式多智能体环境,在这种环境中,一组智能体根据自己的局部观察和共享的全局奖励信号来学习协调其行为,以最大化系统总体收益。
目前主流解决方案是采用集中式训练、分布式执行范式。其中最核心挑战问题在于多智能体信度分配:如何为单个智能体的策略分配属于它自身的贡献,从而更好地协调以最大化全局奖励。
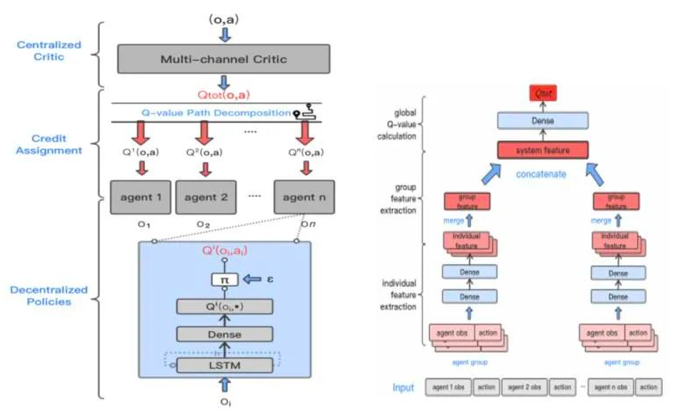
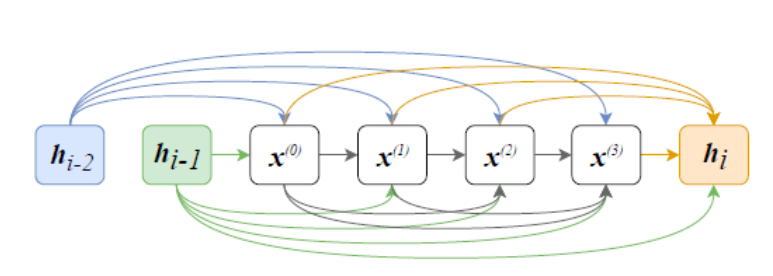
在本文中,我们提出了一种Q值路径分解(QPD)的信度分配机制,可以将系统的全局Q值自动分解为单个智能体的Q值(如图所示)。和先前工作通过显示限制单个Q值和全局Q值的表示关系不同,我们首次将累积梯度归因技术运用到深度MARL中,通过沿轨迹路径直接分解全局Q值来为智能体进行信度分配,并从理论上证明该分配方式下单个智能体的Q值和等于全局Q值。
我们在具有挑战性的《星际争霸II》微观管理任务上评估了QPD,表明其与现有SOTA的MARL算法相比,QPD在同质和异质的多智能体场景中均达到了先进的性能。
一种基于行列式点过程的多智能体学习算法
现有的多智能体算法在对智能体的centralized joint Q-function做factorization的时候都需要假设每个智能体的Q_i和 Q_joint之间的关系,例如VDN假设相加性,Qmix假设单调性。
本文中,我们设计了一种基于行列式点过程的Q_joint的描述方法,在不需要做任何假设的情况下,Q_joint可以通过行列式点过程所描述的行为多样性而自动被factorize成各自的Q_i。
给定N个物品(Item)的集合Y,每个物品 i 有自己的特征向量 wi,这个集合有 2N 个子集,存在一个行列式刻画任意一个子集被选中的概率。行列式点过程( Determinantal Point Process , DPP ) ,将复杂的概率计算转换成简单的行列式计算,通过核矩阵(Kernel Matrix) L 的行列式计算每一个子集的概率。
从直觉上来说,满足 DPP 的过程一般有一个性质是,相似的两个元素同时出现的概率是比较小的。基于此,我们提出一个Q-DPP,用作多智能体学习中联合Q值(Joint Q Value,Q(o, a))的函数估计器(Function Approximator)。
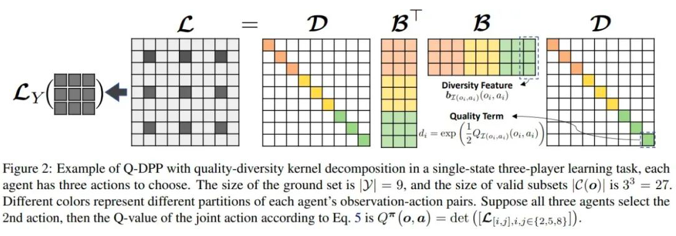
在Q-DPP中,我们可以把每个智能体(Agent)i 的观测向量(Observation)和动作 (Action)(oi, ai) 看做一个item,每个智能体的所有观测与动作的集合可以看做一个分区(Partition),给定所有智能体的观测的情况下,采样出联合动作 (Joint Action) 的过程可以看做从每个分区采样一个 (oi, ai) item的过程。
最后通过采样的联合动作计算 log det得到联合动作的Q值。我们通过将大的核矩阵分解为质量(Quality)和多样性(Diversity)矩阵, Quality 矩阵是由每个智能体的的独立Q值构成(Qi (oi, ai)),Diversity矩阵由需要学习的 (oi, ai) 的多样性特征向量构成,来综合考虑智能体各自收益和总体的多样性。通过这种方式,我们可以自然地将 Q(o, a) 分解为quality和diversity两部分。
基于图感知逻辑回归和抢占式查询候选集生成的属性图上主动学习策略
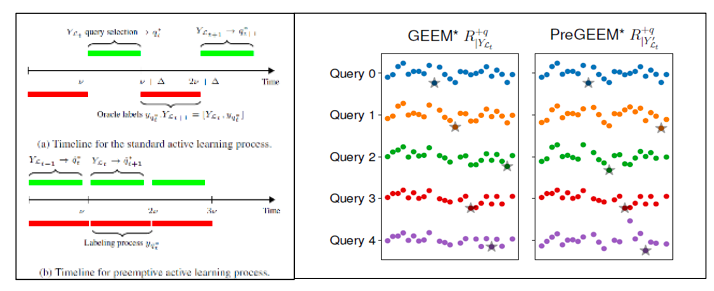
左图: 常规主动学习算法 vs. 抢占式主动学习. 右图: GEEM vs PreGEEM 对于下一个打标签节点risk预估值对比.
对于(含节点属性)图网络中的节点分类问题是分类问题中的一项重要任务,但通常获取节点标签较为困难或昂贵,在有限可标注数据的预算下通常通过主动学习可以提高分类性能。
在图网络结构数据中最好的现有方法是基于图神经网络,但是它们通常表现不佳除非有大量可用的标记节点作为验证集以选择一组合适的超参数。在这个工作中特别针对属性图中的节点分类任务,我们提出了一种基于图的主动学习算法Graph Expected Error Minimization (GEEM)。
我们的算法在预测阶段使用了一种不需要依靠验证集调整超参的线性化图卷积神经网络(linear-GCN),并在主动学习查询标签阶段利用最小化预期误差的目标函数作为选择下一目标label节点的标准。
算法主要包括两个阶段1)在模型预测阶段,我们提出使用线性化的GCN模型获取经验标签(预测标签) 2)在获取下一label节点过程中,我们提出通过对未标记集合上节点的平均错误概率来计算预期误差并作为风险预估标准,从而选择增加此节点后经验风险最小的节点进行label。
为了减少在为候选节点打标签过程带来的延迟(在医疗等需要细节domain knowledge的场景,打标签过程潜在会超过10分钟),我们推导出了GEEM的抢占式查询候选集生成主动学习算法并称为PreGEEM,它在查询/打标签过程中计算下一个候选打标签的对象。
同时,我们在论文中提供了关于PreGEEM风险误差的理论边界。最后,为了解决从几乎从没有标签数据开始学习的情况,我们提供了一种基于标签传播和线性化GCN推理的混合算法,进行自适应模型平均。
我们在四个公开数据集上进行了实验验证,展示出了在各种实验设定下与SOTA算法相比的明显提升,特别是当初始标签集非常有限时我们的模型明显优于其他方法。此外该技术在通信网络中具有潜在的实用价值,例如在初始标签集稀缺时的通信网络中故障链路识别场景中。
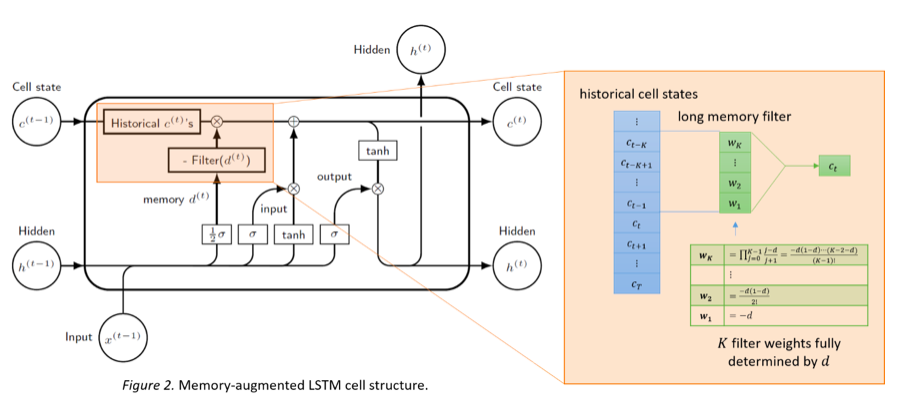
RNN和LSTM有长期记忆吗?
为了克服递归网络(RNN)学习长期依赖的困难,长短期记忆(LSTM)网络于1997年被提出并后续在应用方面取得了重大进展。
长期记忆这个词虽然在深度学习领域并没有严格的定义,但是在统计领域早已有之。本文提出了能够写成马尔科夫链的递归网络不具备长期记忆的充分条件。推理显示,在无外部变量作为输入时,RNN和LSTM的输出一般不具备统计意义上的长期记忆。
本文又将统计学的定义拓展到了深度学习领域。根据新定义,RNN依然不具备长期记忆,而LSTM模型较复杂无法直接分析。若假设LSTM的门不随时间变化,则LSTM也不具备长期记忆。
根据上述理论成果,我们对RNN和LSTM做出最小程度的修改,使其获得对长期相关性建模的能力。类似于ARFIMA模型中的结构,我们分别在RNN的输入和LSTM的状态单元处添加了一个长期记忆滤波器,得到记忆增强RNN和记忆增强LSTM模型。
实验表明,MRNN在长期记忆时间序列预测问题上有明显优势。而由一层MLSTM单元和一层LSTM单元组成的双层网络在论文评议数据集的分类任务上的效果远好于一个两层LSTM网络。
文章链接:https://arxiv.org/abs/2006.03860
开源代码:https://github.com/huawei-noah/noah-research/tree/master/mRNN-mLSTM
【与香港大学联合研究工作】
Neural Architecture Search in a Proxy Validation Loss Landscape
本文通过最小化验证损失代理来搜索最佳神经网络结构。现有的神经结构搜索(NAS)方法在给定最新的网络权重的情况下发现基于验证样本的最佳神经网络结构。但是,由于在NAS中需要多次重复进行反向传播,使用大量验证样本进行反向传播可能会非常耗时。
在本文中,我们建议通过学习从神经网络结构到对应的损失的映射来近似验证损失情况。因此,可以很容易地将最佳神经网络结构识别为该代理验证损失范围的最小值。同时,本文进一步提出了一种新的采样策略,可以有效地近似损失情况。
理论分析表明,与均匀采样相比,我们的采样策略可以达到更低的错误率和更低的标签复杂度。在标准数据集上的实验结果表明,通过本方法进行神经结构搜索可以在较低的搜索时间内搜索到精度很高的网络结构。
Lower Complexity Bounds for Finite-Sum Convex-Concave Minimax Optimization Problems
这个工作主要考虑如下的minimax优化问题:
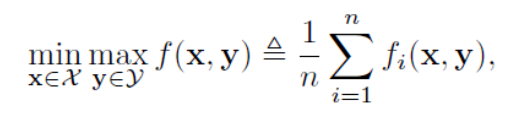
其中每一个fi是L光滑并且关于x凸,关于y凹的函数,这个优化方程包含了多个流行的机器学习应用问题,例如:regularized empirical risk minimization,AUC maximization,robust optimization 和reinforcement learning。
我们的工作主要针对通常被用来解决这一优化问题的随机一阶方法,即Proximal Incremental First-order Oracle (PIFO)来进行统计分析,目标是要找到一个距离该问题的真实解足够接近的鞍点(ε-saddle point)。

我们在文章中证明了PIFO算法至少需要
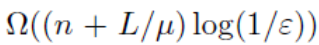
复杂度来找到这个鞍点,这里需要的条件是fi需要L-smooth以及μ-strongly-convex-μ-strongly-concave,而作为范围更广的IFO算法,有前人证明了它所需要的上界同样是该值,所以这个下界是精确的最优下界。
同时也说明,加入额外的stochastic proximal操作并不会减少所需要的样本复杂度。更进一步,我们对非μ-strongly-convex-μ-strongly-concave的另外两种情况,也给出了相应的复杂度下界。
这些结果都得益于我们提出了一种新的下界分析框架,我们的构造把Nesterov’s classical tridiagonal matrix分解为n个组来促进对IFO和PIFO的理论分析。
【与北京大学联合研究工作】