和想象不太一样的'Graph Neural Network + Zero Shot'
今天又琢磨琢磨了,觉得 GNN 真的好适合做 Zero shot 相关的任务呀,觉得真有意思。从最基本的图像分类任务来说,输入 X,我们一般都是直接输入到一个神经网络 NN 里,然后对提取的特征 Y 进行分类。
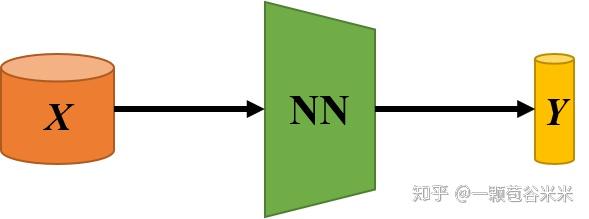
同理,多个类也是输入到同一个 NN 里,进行训练:

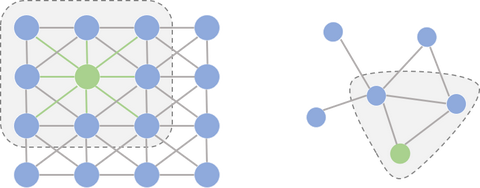
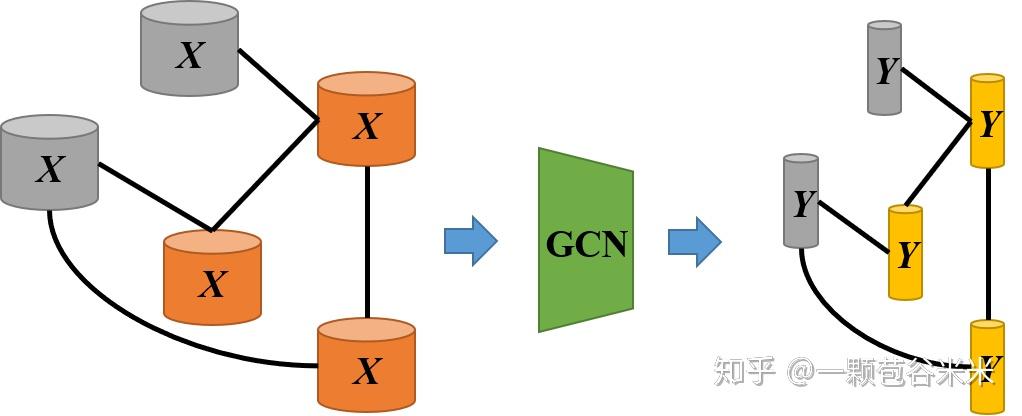
一般输入之间会有一些联系,就存在一些结构信息,我们在提取各个输入的特征向量的时候,如果可以兼顾他们类之间的关系,对分类结果效果更好。但是怎么对这种连接后的 GNN 进行特征提取呢,所以就引入了图卷积神经网络,既对每一个结点的特征进行提取,还保留了结点之间的结构关系。

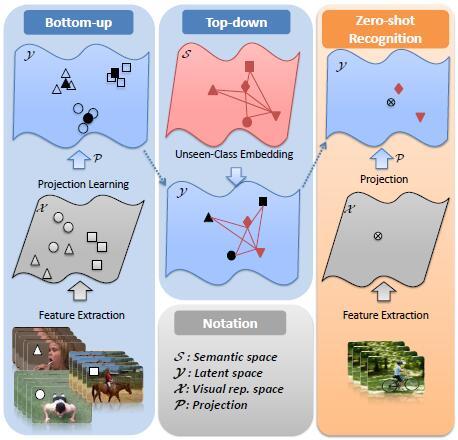
那对于 ZSL 来说,有很多 unseen 类是没有 label 信息进行监督学习的,所以我们一般需要引入 attribute 之类的 semantic 信息。往往这些 unseen 类和 seen 类之间又要一些关联,通过对他们构成的图进行学习,结构信息可以提供很大的帮助。所以重点是如何构建一个图,以及 semantic 信息的融合等。
================ 原文章 ================================
这两年图网络(Graph Neural Network, GNN)炒的很火呀,上次看了一篇文章,以为图网络是那样的,结果这段时间看了些 GNN 在 Zero-shot recognition 上的一些文章,发现和我的想象差别好大呀。下面就分享一点最近看的相关文章:
一颗苞谷米米:图网络与 Zero-Shot Learning 的邂逅
GNN 涉及到一些如拉普拉斯矩阵(Laplacian Matrix)、图卷积(Graph Convolution)等相关的概念,需要了解一下,不然直接看 GNN 会一头雾水。作者 SivilTaram 写的博客比较详细易读,我在看的时候做了 PPT,这里就以图片的形式展示啦~
从图 (Graph) 到图卷积(Graph Convolution):漫谈图神经网络模型 (二)
图网络中涉及的图,一般是无向图。可以用一个邻接矩阵 (Adjacency Matrix
) 来表示每个结点之间的连接关系。通过一系列简单的操作,可以得到拉普拉斯矩阵 (Laplacian Matrix
)。
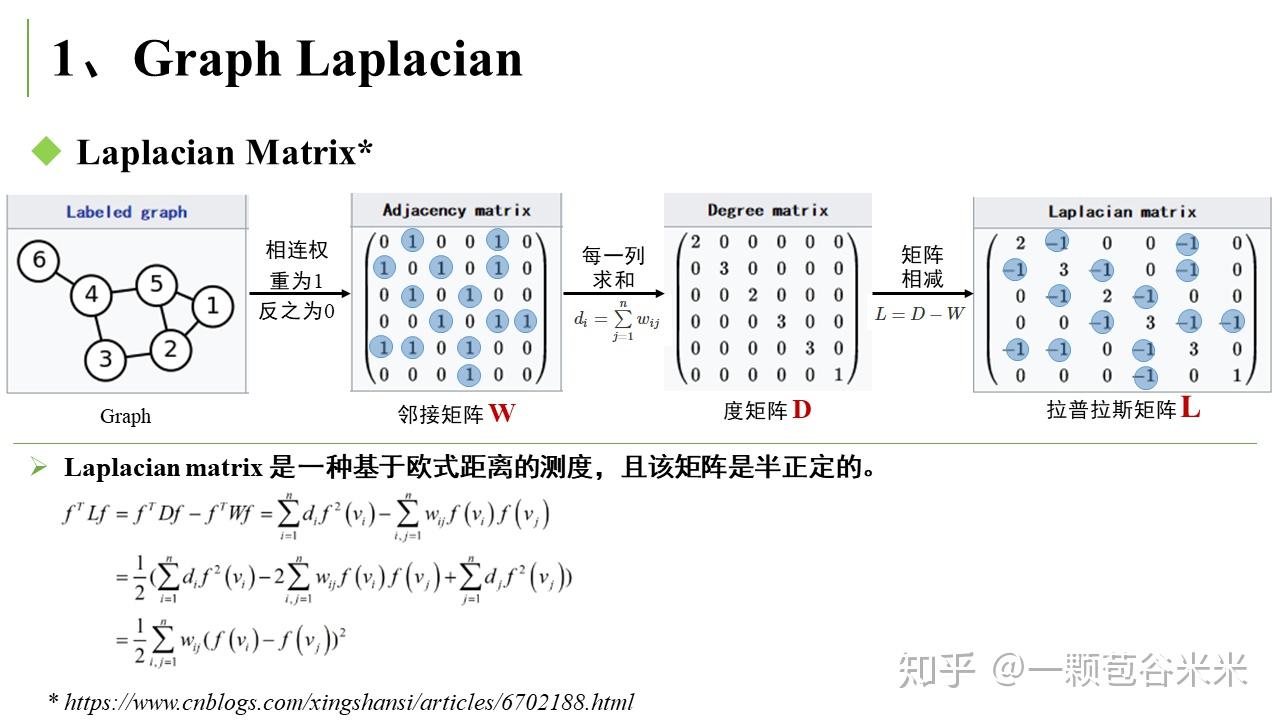
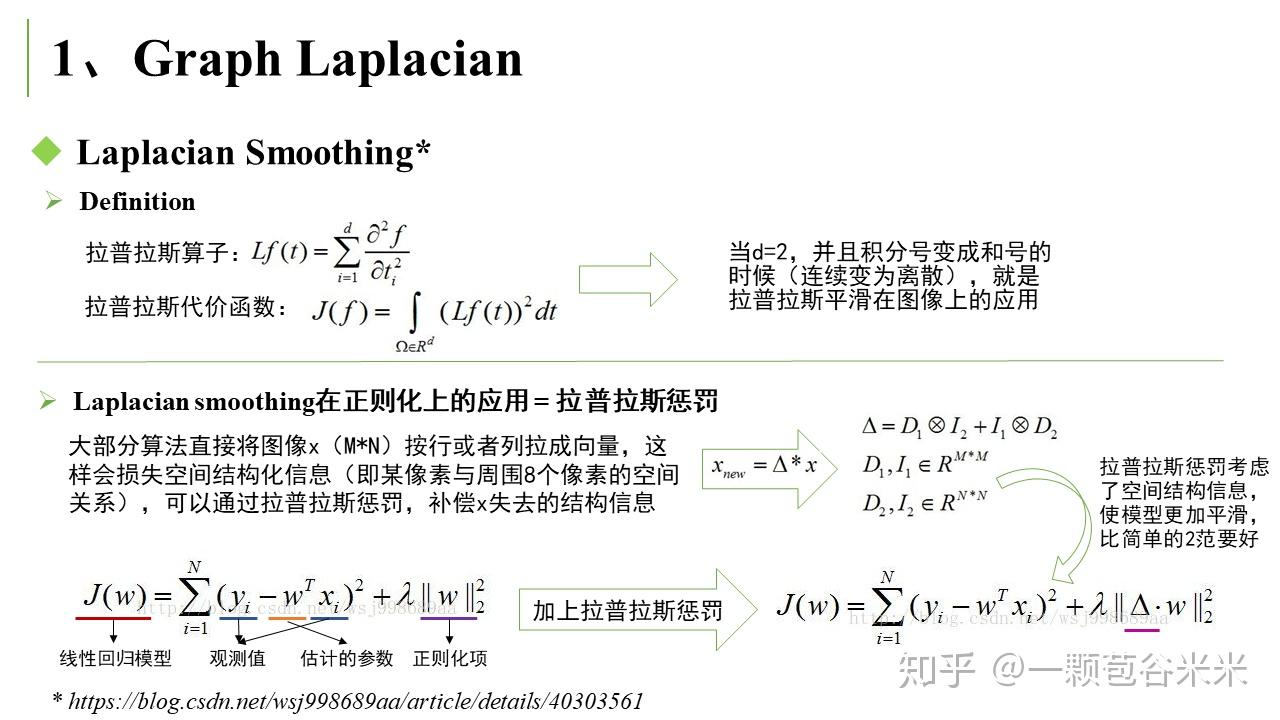
然后是常见的 Graph Convolution,这和我们平时常用的卷积有很大区别,下面会提到空域卷积和频域卷积:
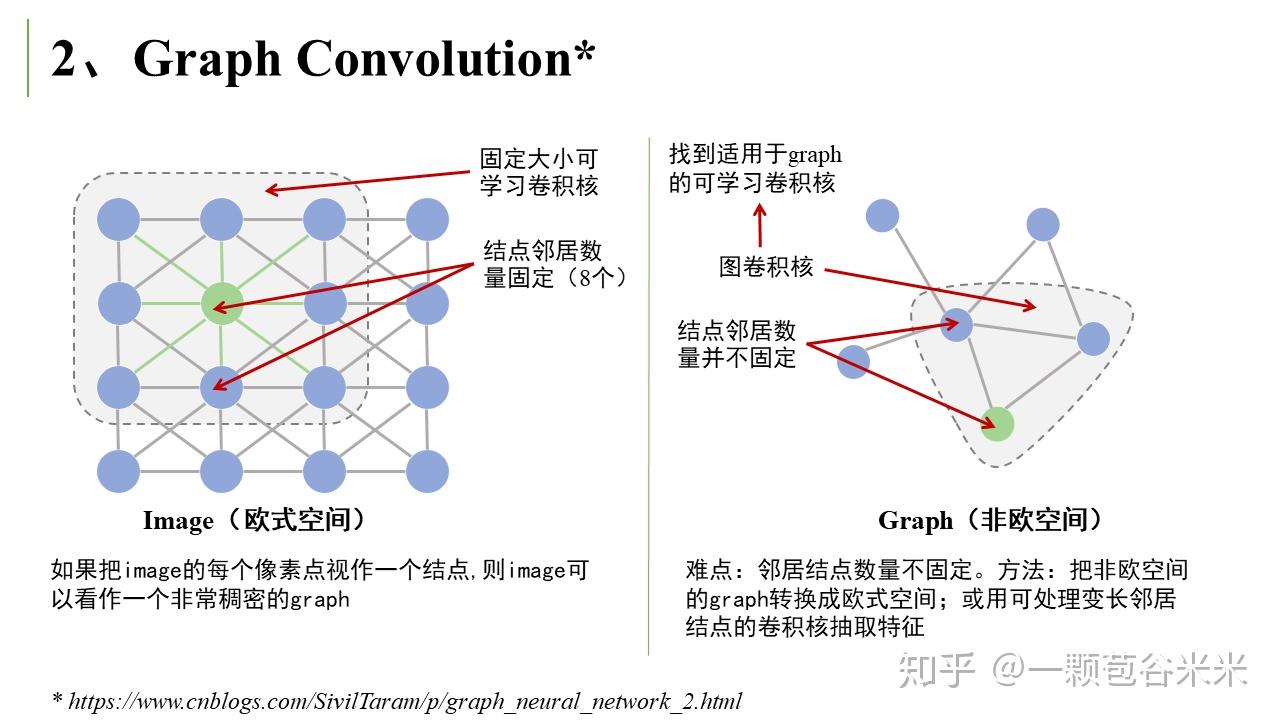
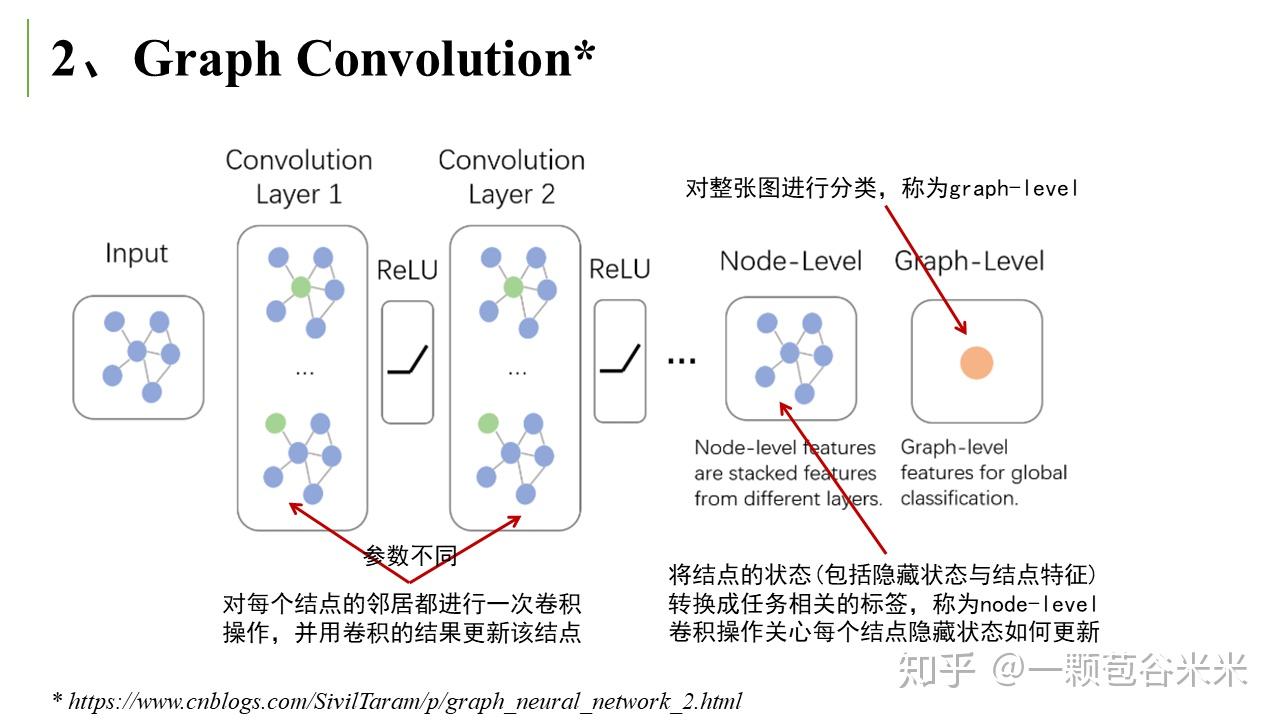

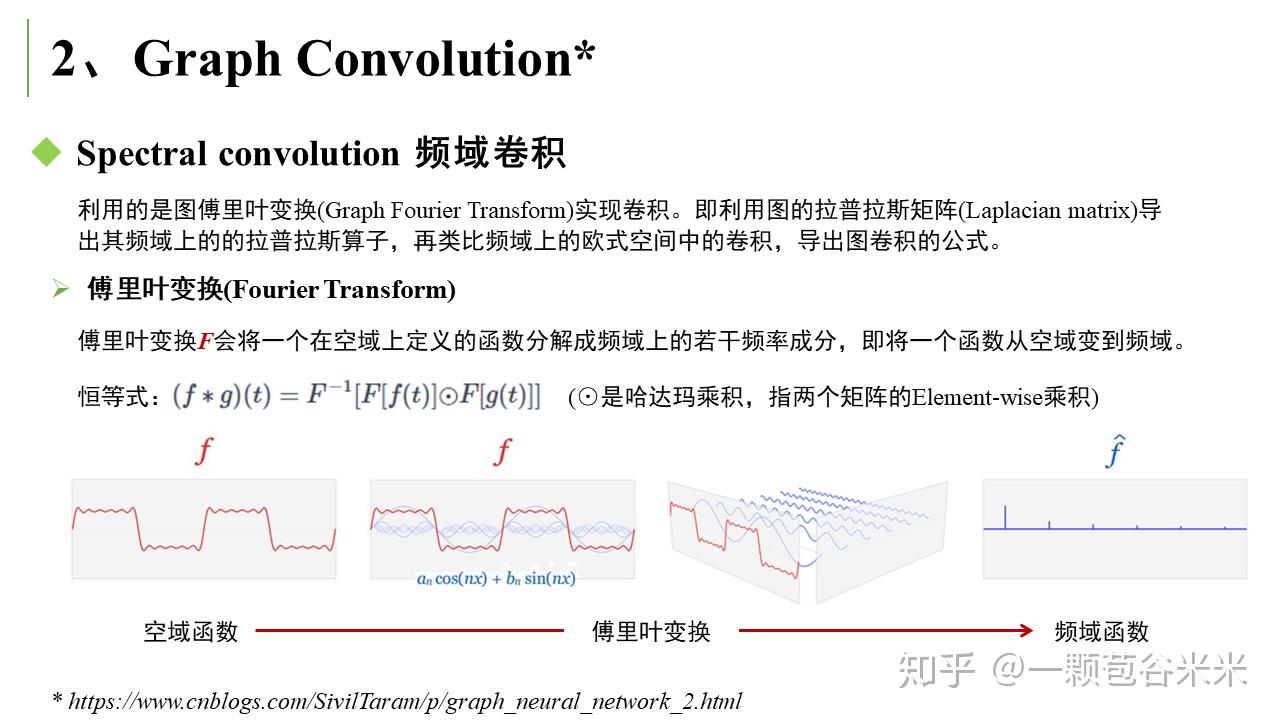
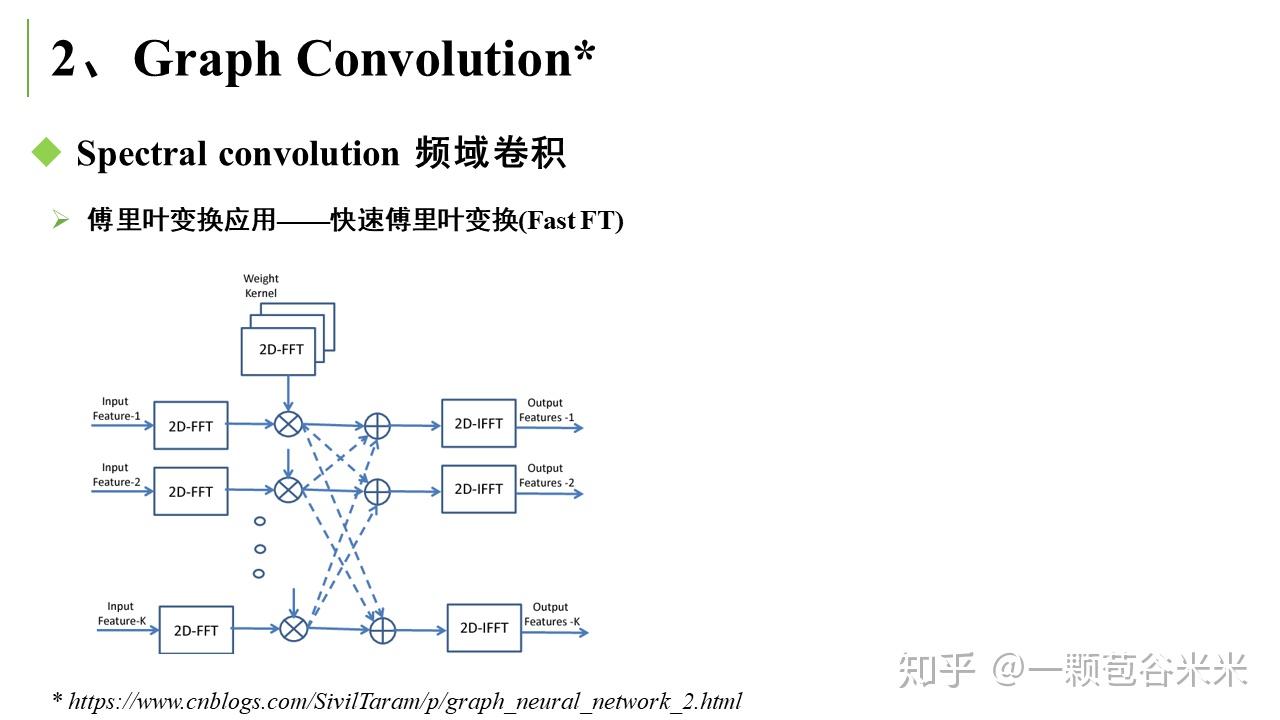
空域卷积非常直观地借鉴了图像里的卷积操作,但缺乏一定的理论基础。相比于空域卷积,频域卷积主要利用的是图傅里叶变换 (Graph Fourier Transform) 实现卷积 。这里又大概说下傅里叶变换的相关知识。




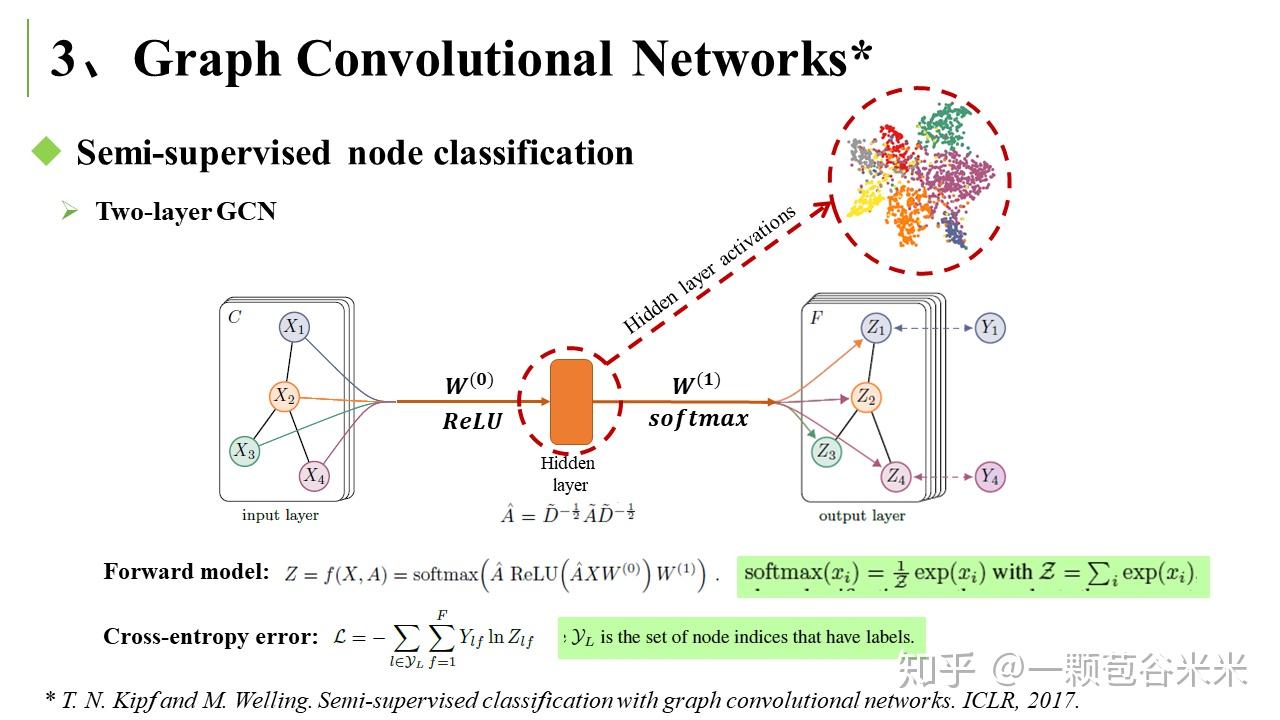
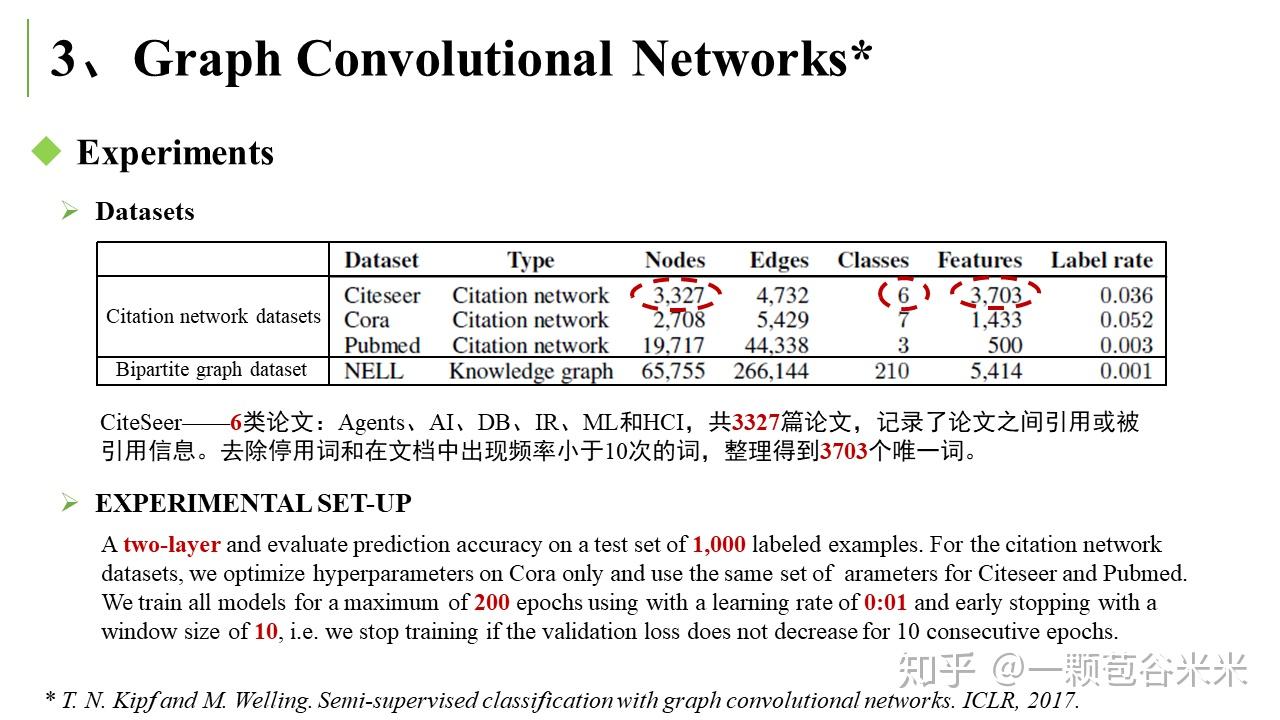
下面就简单说说看的两篇文章,第一篇是将 Graph Convolutional Networks 用于半监督学习中(T. N. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks. ICLR, 2017)。在该文章的应用中,Labels are only available for a small subset classifying nodes in a graph. 文章有很多前面提到的拉普拉斯相关的公式推导:




而另一篇是用图卷积网络结合 semantic embedding 和 categorical relationship 来做 Zero-shot recognition 任务的(X. Wang, Y. Ye, and A. Gupta. Zero-shot recognition via semantic embeddings and knowledge graphs. CVPR 2018)。

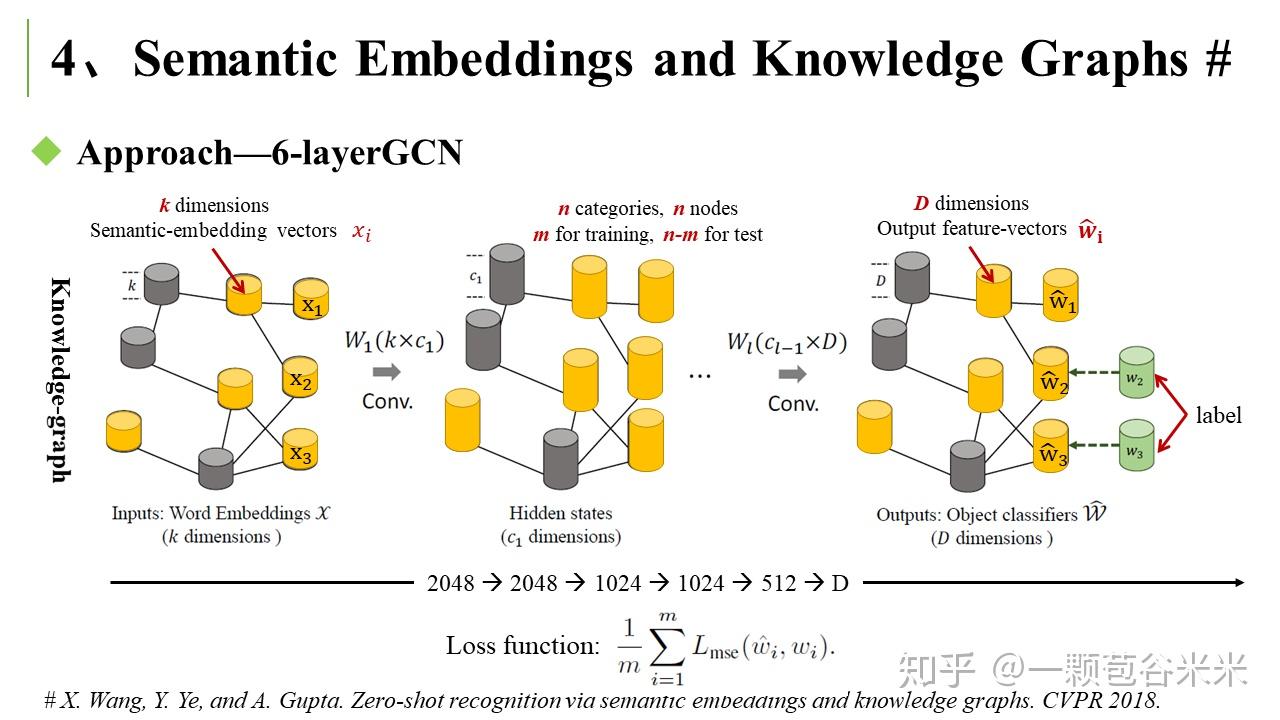
这个思路比较简单,用一个知识图来表示明确的关系。其中结点是 semantic category ,边就是他们之间的 relationship。通过对 seen 类的监督学习来更新整个 knowledge graph。
总的来说,前面提到的任务,都是有一个构建好的 knowledge graph,并有大部分结点具有 label 信息。通过基于傅里叶变换 (Fourier Transform) 的频域 graph convolution 操作,来将 seen 类中学习到的知识,迁移到 unseen 类上。如何构建一个好的图就很关键啦,然后就是 graph convolution 结构和 loss 函数的设计也很重要。这一块还是有很多值得研究的。因为这一块,我看的并不是很透彻,今天这个就先写到这里了。下面还是要回头恶补一下 Graph Neural Network 的知识,然后抓紧实现我的想法啦~
好新的文章。可惜我不懂迁移学习。只懂点卷积。
这和 image 的卷积也还有点差别 哈哈哈 蛮有意思的
图网络中涉及的图,一般是无向图。可以用一个邻接矩阵 (Adjacency Matrix ) 来表示每个结点之间的连接关系。通过一系列简单的操作,可以得到拉普拉斯矩阵 (Laplacian Matrix  。我刚才的问题就比如说这句话里面的结点,在图片分类中是不是就指的像素点。我看过 16 年那篇文章,作者用 mnist 28✘28 的图片。共 784 个像素点用 knn 方法取 8 个最近点然后一系列(我还没看完) 构造了邻接矩阵。那这个矩阵其实就是提取或者有了图片的像素点 (结点) 之间的结构信息吗?打扰了
博主文章中用到的 graph 截图来源能分享下么
https://www.cnblogs.com/SivilTaram/p/graph_neural_network_2.html
这个网页哈
博主你好,我特别特别想问一个问题。就是对于传统的 mnist 这种图片数据,如果用图卷积 (目前我唯一看过的代码,16 年的) 做分类。那你文章说的一个结点是指每一个图片的一个像素点吗???那图卷积用于图片分类,挖掘的结构信息就是单个图片内像素点之间的结构信息吗?非常感谢。
不好意思啊,之前没注意到消息。上面只是对比用于 image 的常用的卷积,将每个像素当作一个结点,只是想说明图卷积的每个结点的邻结点的个数是不确定的,所以不能像 CNN 那样做卷积。一般做图像分类,每一个结点应该是代表一个类别,如 mnist,就 10 个结点,其结构信息应该是两个类间的信息,如 0 和 6、8 可能会有连接,4、7、9 会有连接的那种。
你好,很感谢这篇文章的总结,但我个人实验发现图卷积并不太适合 zsl,因为图卷积的本质还是对节点进行平滑处理,一旦对 semantic label 进行平滑后,将会导致潜空间的嵌入向量不具有区分性,降低精度。。。 不同于其他任务,zsl 要求语义嵌入向量即要保持语义关系,又要保持足够的可区分性。
这点在 CVPR19:Rethinking Knowledge Graph Propagation for Zero-Shot Learning 也谈到过这个问题,因为平滑问题,cvpr18 的那篇文章 gc 只用到了一层。。。 事实上我个人实验感觉 一层都不能用。。。可能是我对 GCN 的了解太浅薄了,我的邻接矩阵是用语义标签之间的 cosine distance 求得,不知道会不会是我邻接矩阵弄得不好?
我还正在试验当中,你说那篇 cvpr2019 的我也没看过,我去去看看哈。
如果在之前做 zsl 的基础上,把图作为一个辅助 loss 呢会不会好点。
关于邻接矩阵我最近也在思考,相较于神经网络,图网络在提取特征的情况下,还保持了很强的先验结构知识。对于 zsl 问题来说,label 与 attribute 之间的结构关系构建好了,应该是可以对 zsl 问题的解决有所帮助的。我看很多地方都是用 word embedding 来构建知识图,这对 zsl 并不是很受用。但我自己还在实验中,还不是很确定。
谢谢你的讨论~
噢噢噢,我刚刚去看了那个论文,想起我之前看过的。他做的这个 Zero shot learning 跟我们平时做的那些 ZSL,我觉得还是有区别的。他用的 ImageNet 数据集,官方提供了一个树形结构的图,来表示两个类别之间的一种结构关系,会涉及到父代、子代的从属关系,通过这个树来做 unseen 类的识别。好像是没有涉及 attribute 这一类的语义信息。