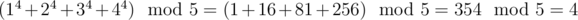让求出 (1^n + 2^n + 3^n + 4^n )mod 5 的结果,而n最大能够有10^5位数。仅仅能用字符串来存,将取模分开得到
1^n mod 5 = 1 ;
2^n mod 5 = 随着n从0開始,结果为 1 2 4 3 1 2 4 3 1 2 4 3 。。
。。以1 2 4 3 循环
3^n mod 5 = 随着n从0開始。结果为 1 3 4 2 1 3 4 2 1 3 4 2.。
。
。。以1 3 4 2 循环
4^n mod 5 = 。。
。。结果为 1 4 1 4 1 4 以1 4 循环
求给出的n是奇数还是偶数,方法推断最后一位奇数偶数。
再求解n mod 4 。方法求出最后两位的对4取模的值
#include <cstdio>
#include <cstring>
char str[110000] ;
int main()
{
int ans = 1 , l , i , k ;
scanf("%s", str);
l = strlen(str);
if( (str[l-1]-'0')%2 )
ans += 4 ;
else
ans += 1 ;
if( l-1 != -1 )
k = ( str[l-1]-'0' );
if( l-2 != -1 )
k = k + (str[l-2]-'0')*10 ;
if( k%4 == 0 )
ans += 2 ;
else if( k%4==1 )
ans += 5 ;
else if( k%4 ==2 )
ans += 8 ;
else
ans += 5 ;
printf("%d
", ans%5);
return 0;
}