mport numpy as np #数据包
import scipy
from scipy import stats
import matplotlib as mpl
import matplotlib.pyplot as plt #画图
# # 1. 数据的形成
x = np.arange(0,51,10).reshape((-1,1))
# b
# [[ 0]
# [10]
# [20]
# [30]
# [40]
# [50]]
a =np.arange(0,51,10).reshape((-1,1))+ np.arange(0,5,1)
# a
# [[ 0 1 2 3 4]
# [10 11 12 13 14]
# [20 21 22 23 24]
# [30 31 32 33 34]
# [40 41 42 43 44]
# [50 51 52 53 54]]
c = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
# c
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
c.shape = 2,-1
# c
# [[ 1 2 3 4 5 6]
# [ 7 8 9 10 11 12]]
d = c.reshape((3,-1))
# d
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
e = np.array([[1,2,3],[4,5,6],[7,8,9],[10.5,11,12]],dtype=np.float)
# e
# [[ 1. 2. 3. ]
# [ 4. 5. 6. ]
# [ 7. 8. 9. ]
# [10.5 11. 12. ]]
f = e.astype(np.int)
# f
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
# #linspace函数通过指定起始值,终止值和元素个数来创建数组,区别:arange最后一个参数是步长,这个是个数
a = np.linspace(0,10,15) #等差数列
# a
# [ 0. 0.71428571 1.42857143 2.14285714 2.85714286 3.57142857
# 4.28571429 5. 5.71428571 6.42857143 7.14285714 7.85714286
# 8.57142857 9.28571429 10. ]
# len(a) = 15
b = np.linspace(0,10,10,endpoint=False) #endpoint 为False时不包含终止值
# b
# [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
# #logspace 可创建等比数列
#下面函数创造的是base = 10(10进制)起始值是10^0,终止值10^2,个数为4的等比数列
a = np.logspace(0,2,4)
# a
# [ 1. 4.64158883 21.5443469 100. ]
# #base = 2 则是二进制的数据 起始值2^0,终止值2^5,个数为6
b = np.logspace(0,5,6,base=2)
# b
# [ 1. 2. 4. 8. 16. 32.]
# # 使用frombuffer,fromstring,fromfile等函数可以从字节序列创建数组
s = 'abcd'
# g = np.fromstring(s,dtype = np.int8)
# g
# [ 97 98 99 100]
# #
a = np.array([1,3,5,7,9,11])
b = np.array([1,3,5])
# a[b]
# [ 3 7 11]
# # np.random.rand() 取[0,1)中均匀分布的随机数
a = np.random.rand(12)
# a
# [0.8521443 0.59647865 0.80059422 0.93992606 0.37162934 0.37548125
# 0.40950715 0.40181645 0.72717888 0.25377955 0.38971442 0.98884064]
# a>0.5
# [ True True True True False False False False True False False True]
# a[a>0.5]
# [0.8521443 0.59647865 0.80059422 0.93992606 0.72717888 0.98884064]
a = np.arange(0,51,10) #行向量
# a # a+[1,3,5,7,9,10]
# [ 0 10 20 30 40 50] # [ 1 13 25 37 49 60]
b = a.reshape((-1,1)) #转化成1列的 相当于转化成了列向量
# b b+[1,3,5,7,9,10]
# [[ 0] [[ 1 3 5 7 9 10]
# [10] [11 13 15 17 19 20]
# [20] [21 23 25 27 29 30]
# [30] [31 33 35 37 39 40]
# [40] [41 43 45 47 49 50]
# [50]] [51 53 55 57 59 60]]
# # 二维数组切片
a = np.arange(0,50,10).reshape((-1,1)) + np.arange(0,5,1)
# a a[(0,1,2),2:] a[(1,2,3),(0,1,2)]
# [[ 0 1 2 3 4] [[ 2 3 4] [10 21 32]
# [10 11 12 13 14] [12 13 14]
# [20 21 22 23 24] [22 23 24]]
# [30 31 32 33 34]
# [40 41 42 43 44]]
# #绘图
# 绘制正态分布概率密度函数
# E = 0 #均值
# q = 1 #标准差
# x = np.linspace(E - 3 * q, E + 3 * q, 55)
# y = np.exp(- (x - E) ** 2 / (2 * q ** 2)) / (q * np.sqrt(np.pi))
# y2 = 0.1 * x + 0.2
# print(x)
# print(y)
# print(y.shape)
# plot1 = plt.plot(x,y,'r-',x,y,'go',label = 'myline1',linewidth = 1, markersize = 2) #'r-'是red的线,'go'是指green的圈(点)
# plot2 = plt.plot(x,y2,'y-',x,y2,'bo',label = 'myline2',linewidth = 1, markersize = 2)
# plt.legend(loc = 'upper right') #将label显示在右上角'upper right'
#
# plt.grid(True) #虚线方格
# mpl.rcParams['font.sans-serif'] = [u'SimHei'] #FangSong/黑体
# mpl.rcParams['axes.unicode_minus'] = False #s上面加下面为False就可以显示中文标题了
# plt.title(u'Guess高斯分布') #标题
# plt.savefig('1.png') #保存图片
# plt.show()
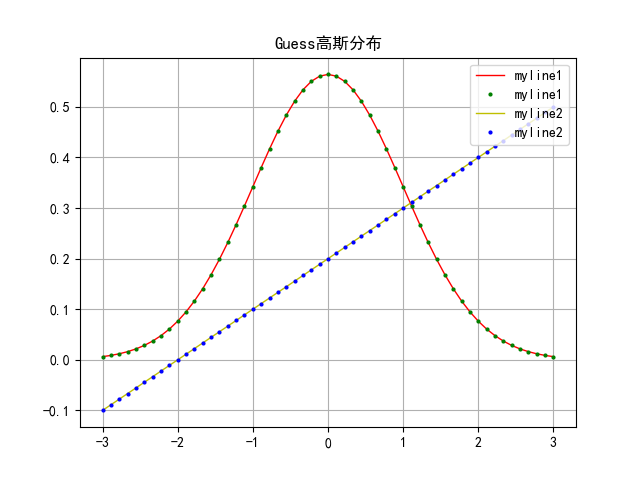
图1
# # 均匀分布
# y = np.random.rand(10000)
# x = np.arange(len(y))
# print(y)
# print(x)
# plt.grid()
# plt.hist(y,30,color = 'r', alpha = 0.7) #柱形图 1-2
# plt.savefig('1-2.png')
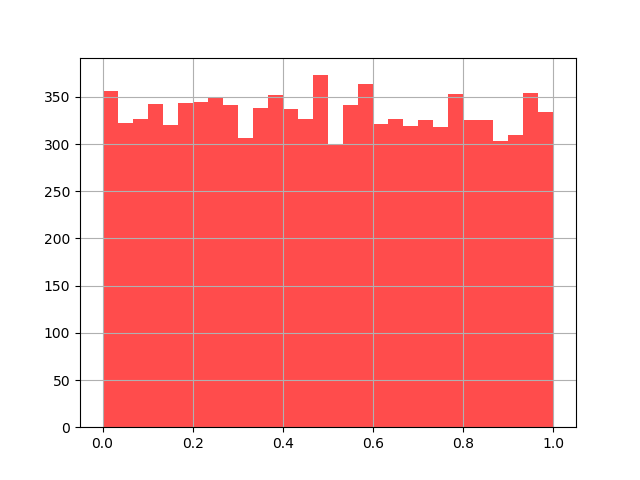
图1-2
# plt.plot(x,y,'r-',label = '均匀') # 1-3
# plt.savefig('1-3.png')
# plt.show()

图1-3
# mu = 2
# sigma = 3
# data = mu + sigma * np.random.randn(1000) #直接生成高斯分布的1000个随机值
# # print(data)
# plt.grid(True)
# h = plt.hist(data,30,normed=1,color='yellow') # x轴分为30份做直方图
# # print(h[1])
# # print(h[0])
# x = h[1]
# y = stats.norm.pdf(x,loc = mu,scale = sigma)
# plt.plot(x,y,'r--',x,y,'bo',linewidth = 1,markersize = 2)
# # plt.savefig('1-4.png')
# plt.show()
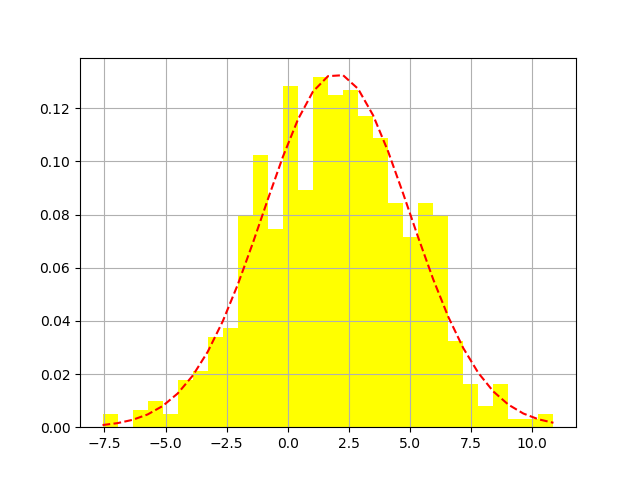
图1-4
# # 利用 scipy 中的 stats.norm.pdf 函数画高斯分布函数 1-5
# E = 0
# q = 1
# x = np.linspace(E - 3 * q,E + 3 * q,60)
#
# y = stats.norm.pdf(x,0,1)
# plt.grid()
# plt.plot(x,y,'r-')
# plt.savefig('1-5')
# plt.show()
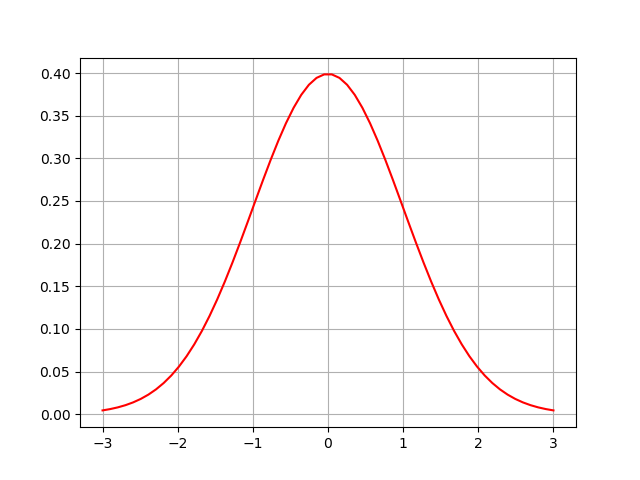
图1-5



