All rights reserved. Please don't share this article without notifying me. Email address: westonhunter@zju.edu.cn
An example of Gram Schmidt Orthogonalisation:
Find one orthonormal set of R^3 given vectors (1,1,0)^T,(-1,1,1)^T,(1,-1,0)^T
These vectors can be organized in a data matrix A:

We denote in this article the k-th column of a matrix A by cAk. Similarly we shall use rAj to refer to the j-th row of A. The first orthogonal basis is
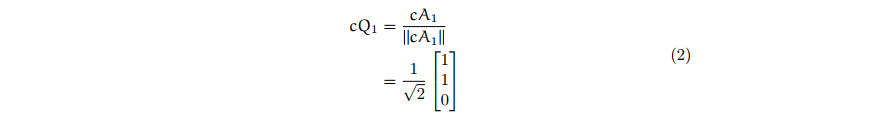
To calculate the 2nd orthogonal basis, we have

And the corresponding orthogonal basis is
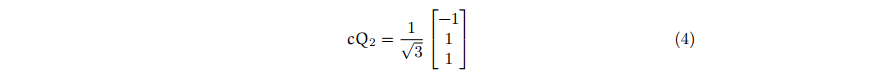
The 3rd intermediate vector
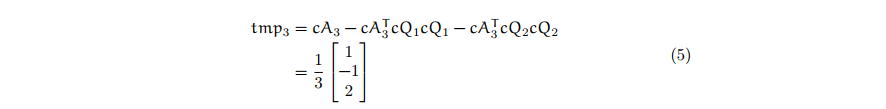
And the 3rd orthogonal basis
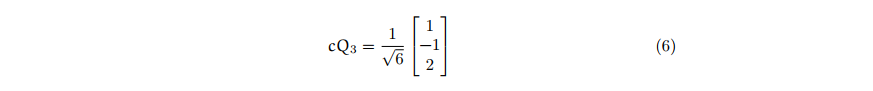
From the calculations above, we have
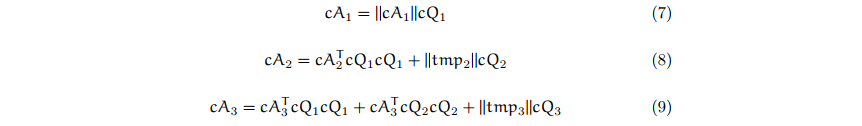
And the corresponding matrix multiplication form is

QR-Decomposition aka QR-factorization definition:
Let A be a real m*n matrix (m>=n). A can be decomposed into the product A=QR where Q (m*n) is orthogonal (Q^TQ=In) and R (n*n) is upper triangular.