教材学习内容总结
书上有的内容我就不重复赘述了,只需要将部分重要的知识点归纳总结一下。
1.进制
- 二进制、八进制、十进制、十六进制(转换:以二进制作为中间变量)
2.字
- 每台计算机都有一个字长,指明整数和指针数据的大小。
- 虚拟地址是以这样的一个字来编码的,字长决定虚拟地址空间的最大范围。
3.字节顺序
- 小端法——在存储器中按照从最低有效字节到最高有效字节的顺序存储对象。
- 大端法——从最高有效字节到最低有效字节的顺序存储。
4.布尔代数
- (1)二进制值是计算机编码、存储、操作信息的核心(0、1),最简单的布尔代数是在二元集合{0,1}上的定义。
- (2)一个布尔代数,是指一个有序的四元组〈B,∨,∧,〉,其中B是一个非空的集合,∨与∧是定义在B上的两个二元运算,是定义在B上的一个一元运算,并且它们满足一定的条件。
- (3)布尔值有两个,真(用1表示)和假(用0表示)。
- (4)布尔值的基本运算是基本逻辑运算,如:逻辑与,逻辑或,逻辑非,异或,同或等等。有自己的一套概念如最大项、最小项、卡诺图、反演律、吸收律之类。
5.整数表示
- 数据类型long long是在ISO C99中引入的。(编译:gcc -std=c99)。
- 64位机器用8个字节表示;32位机器用4个字节表示。
- 负数的范围比整数的范围大1。
6.补码
-补码是最常见的有符号数的计算机表示方式。
- 正数的补码=原码
- 负数的补码=原码各位取反再加1
- 最高有效位也叫符号位。
7.无符号数与有符号数转换
强制类型转换的结果保持位值不变,改变解释这些位的方式。 处理同样字长的有、无符号数之间相互转换的规则:数值可能会变,但是位模式不变。(底层的位表示保持不变)
- 无————>有:U2Tw函数
- 有————>无:T2Uw函数 注:w表示数据类型的位数。
8.扩展数字的位表示
- 零扩展:在开头添0。(将无符号数转换成更大的数据类型)
- 符号扩展:添加最高有效位的值的副本。(一个补码数字转换成更大的数据类型)
9.截断数字
-
可能会改变数值——溢出的一种形式。
-
对于无符号数字x,截断到k位,相当于计算:x mod 2(k)。(k次幂)
10.整数运算
- 整数运算实际上是一种模运算形式。表示数字的有限字长限制了可能的值得取值,结果可能溢出。
- 溢出:一个算术运算的溢出——完整的整数结果不能放到数据类型的字长限制中。
11.浮点数:
标准:IEEE标准754
(1)二进制小数 定点表示法:“.”为界(不能有效的表示很大的数)
十进制:小数点左边的数字的权是10的非负幂,得到整数值;右边的数字的权是10的负幂,得到小数值。 二进制:小数点左边的数字的权是2的非负幂,右边的数字的权是2的负幂。
(2)IEEE浮点表示
- 用V = (-1)s * M * 2E的形式来表示一个数:
符号:s决定这个数是负数(s = 1)还是正数(s = 0),而对于数值0的符号位解释作为特殊情况处理。
尾数:M是一个二进制小数,它的范围是1 ~ 2-ε,或者是0 ~ 1-ε。
阶码:E的作用是对浮点数据加权,这个权重是2的E次幂(可能是负数)。
- 将浮点数的位表示划分为三个字段,分别对这些值进行编码:
一个单独的符号位s直接编码符号s。
k位的阶码字段exp = ek-1…e1e0编码阶码E。
n位小数字段frac = fn-1…f1f0编码尾数M,但是编码出来的值也依赖于阶码字段的值是否等于0。
- 两种常见的格式:C语言中的单精度浮点格式float 和双精度浮点格式double。
在float中,s、exp和frac字段分别为1位、k = 8 位和n = 23位,得到一个32位的表示;
在double中,s、exp和frac字段分别为1位、k = 11 位和n = 52位,得到一个64位的表示。
相关思考
1.从逆向角度考虑为什么无符号数、有符号数(2进制补码)、浮点数之间的转换会产生漏洞?
任何漏洞产生都必然因为系统不可更改的局限性——>无符号数、有符号数、浮点数的局限性——>无符号数或者有符号数的表示范围有限,而浮点数虽然编码范围大,但是不精确。
2.怎么样让负数等于正数?
在负数x后加上U,可以使其转换为(2^w+x)
3.整数与浮点数表示同一个数字的关系?
整数与浮点数表示同一个数字时,化成二进制形式之后,可以看到,整数等于1 的最高有效位之后的数字,与浮点数小数部分的高位是相匹配的
4.当阶码全为1、小数域全为0时,得到的值表示无穷;当阶码全为1、小数域不全为0时,结果是NaN(not a number)
5.整数与浮点数转换规则?
整数->浮点数:整数转换成二进制表示,然后小数点左移若干位得到规格化表示;取出小数部分的数值,在后面补0使其达到23位; 用frac加上偏置量得到的结果用二进制表示,放在取出的部分前面,再加上一个符号位即可。
学习过程及问题
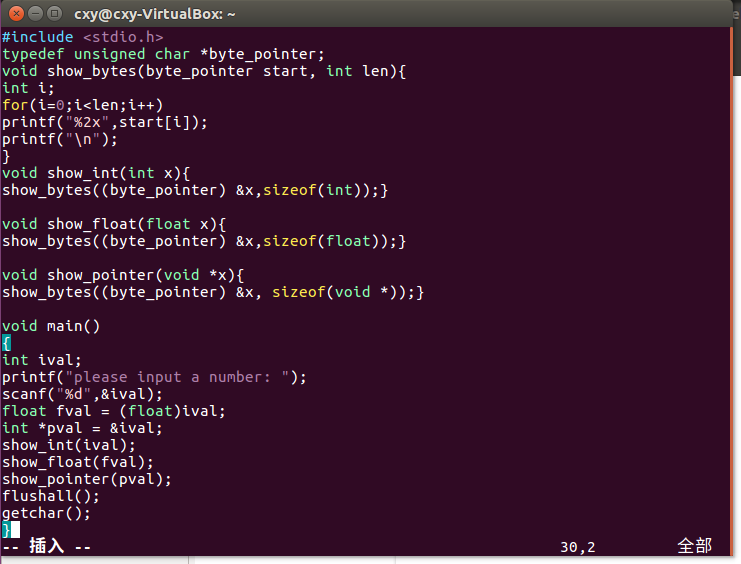
p28的代码我加了个main()函数
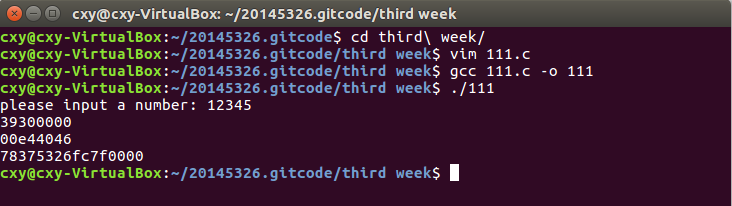
p35的代码用gdb调试练习:
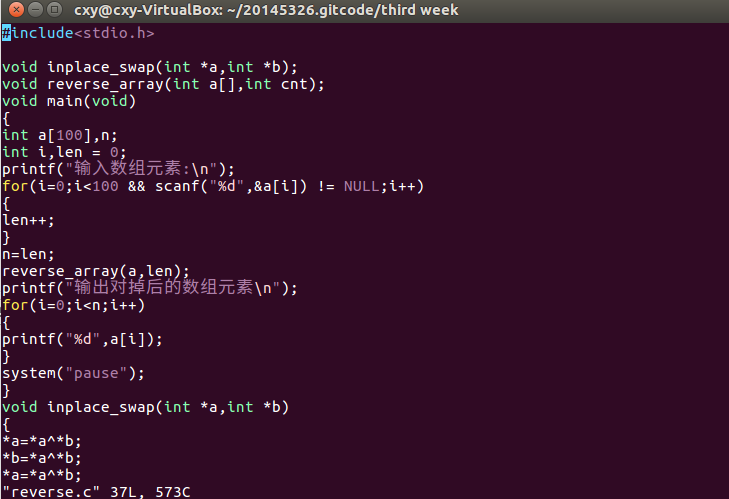

p44的代码运行:

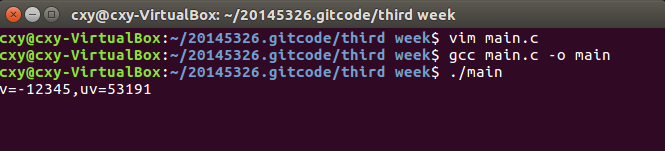
p47的代码编译及gdb调试:


p49的代码编译练习:
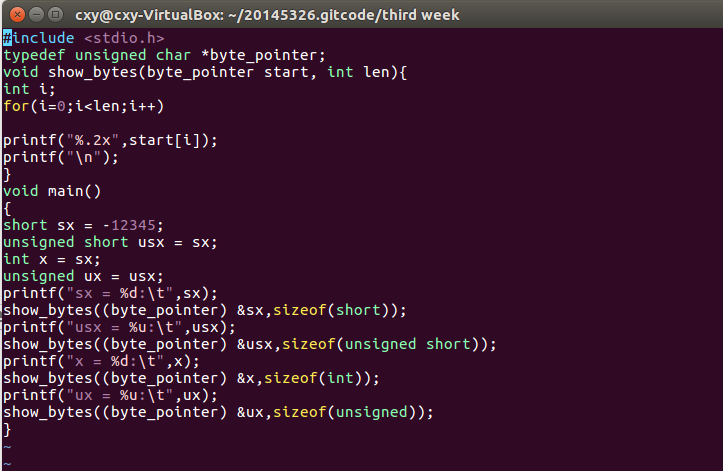
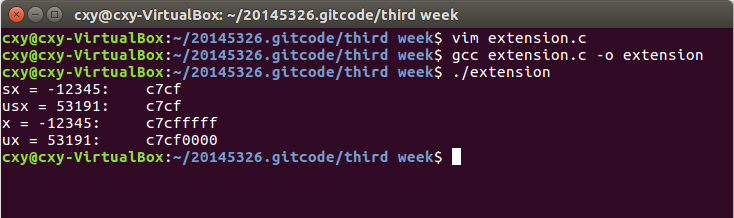
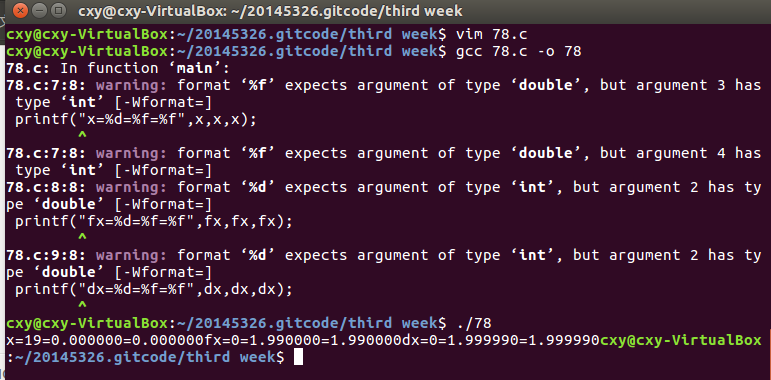
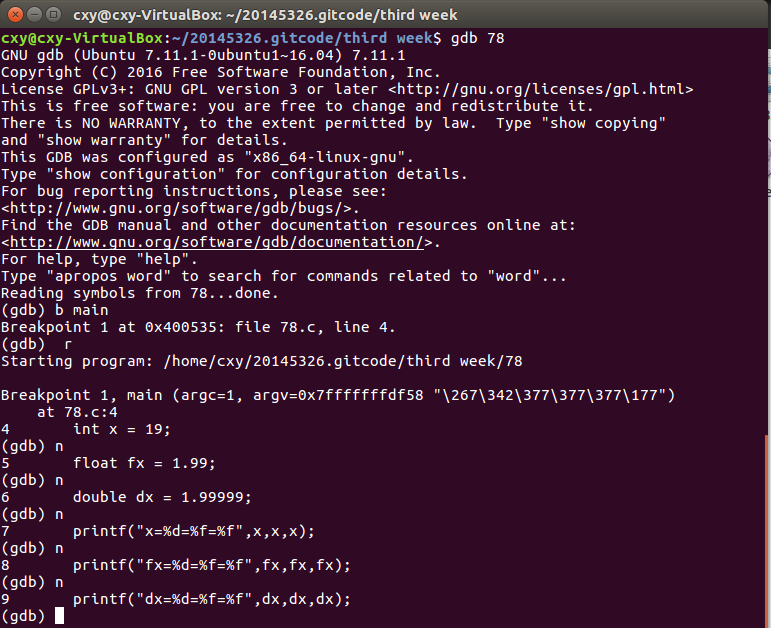
p78的代码编译及练习:
家庭作业
2.56 用不同示例值运行P28代码
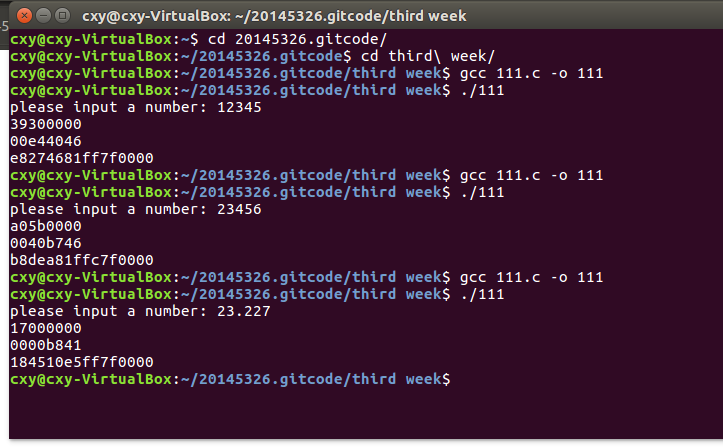
2.59
(x&0xFF) | (y&~0xFF)
2.61

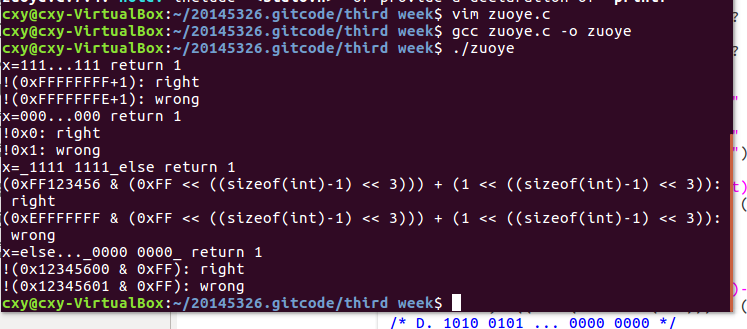
A. !~x
B. !x
C. !~(x>>((sizeof(int)-1)<<3))
D. !(x&0xFF)
代码托管情况
本周所敲代码行数:

心得体会
本周的内容本来也很多,不过根据娄老师给的教材重点,有目的有重心的去看教材,效果会大大提升!也会非常节约时间。不过完全不看教材,一心想走捷径是绝对不行的,这门课本身就需要耗费大量时间来消化。从最开始看教材,熟悉知识点,到看代码,理解代码,到最后自己能调试代码,自己能编写代码。必须得静下心来,投入大量精力与时间,将理论与实践相结合,才能学出效果。任何一门学科都有自身的特点,将其特点与自身的学习风格相结合,打造出一套适合自己的完美学习方法,这至关重要,现在凡事都要讲科学,毫无疑问运用科学的学习方法,学习效率必定大大提高,还能有效的节约时间。何乐而不为?
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/2 | 20/20 | |
| 第二周 | 58/58 | 1/3 | 20/40 | |
| 第三周 | 150/208 | 1/4 | 22/62 |