VLSI芯片测试
1. 芯片测试
在讲解具体的芯片测试的分治策略算法之前,先来了解芯片测试的意思。
1.1 一次测试的过程
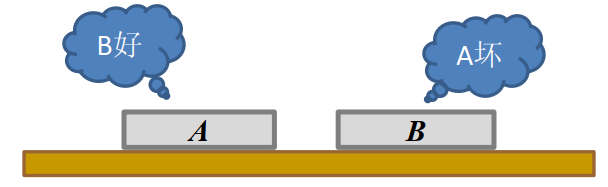
如上图,A、B为芯片。测试方法为:将2片芯片(A和B)置于测试台上,互相进行测试,测试报告是“好”或者“坏”,只取其一。
- 假设:好芯片的报告一定是正确的,坏芯片的报告是不确定的(可能会出错)
那么上述测试的结果有四种可能,如下图:
上面的结果应该不难理解
那么现在问题来了:
- 输入:n片芯片,其中好芯片,至少比坏芯片多一片(要不然测试不了)附:若多于n/2的芯片是坏的,在这种成对测试方法下,使用任何策略都不能确定哪个芯片是好的。
- 问题:设计一种测试方法,通过测试从n片中挑出1片好芯片
- 要求:使用最少的测试次数
1.2 如何测试一块芯片的好坏
针对上述问题,现在先来研究一下,如何在上述n片芯片中,测试出A是好芯片还是坏芯片?
- 问题:给定芯片A,判定A的好坏
- 方法:用其他n-1片芯片对A进行测试。
假设:n=7:好芯片数>=4
- A好,6个芯片中至少3个报“好”
- A坏,6个芯片中至少4个报坏
所以对于n是奇数情况下:好芯片数>=(n+1)/2
A好,至少有(n-1)/2个报“好”
A坏,至少有(n+1)/2个报“坏”
结论:
- 至少一半报好,A是好芯片
- 超过一半报坏,A是坏芯片
假设: n=8:好芯片数>=5
- A好,7个芯片中至少4个报“好”
- A坏,7个芯片中至少5个报“坏”
所以对于n是偶数:好芯片数 >= n/2+1.
A 好, 至少有 n/2个报告“好”
A 坏, 至少有 n/2+1个报告“坏”
结论:n-1份报告中
- 至少一半报好,A是好芯片
- 至少一半报坏,A是坏芯片
上面的分析,已经很清晰,我们已经知道如何测试一块芯片的好坏。那么人们最拿手的方法就是:暴力算法(蛮力算法)。
1.3 蛮力算法
测试算法:任取 1片测试,如果是好芯片,测试结束;如果是坏芯片,抛弃,再从剩下芯片中任取 1片测试,直到得到 1片好芯片
时间估计:
第一片是坏芯片,最多测试n-2次
第二片是坏芯片,最多测试n-3次
…
总计:Θ ( n 2 )
可见时间复杂度之高,数据量一多,肯定会超时。
1.4 分治算法设计思想
在分析分治算法的正确性之前,我们先给出这个算法的描述:
假设n为偶数,将n片芯片两两一组做测试淘汰,剩下芯片构成子问题,进入下一轮分组淘汰。
淘汰规则为:
- “好,好” ==> 任留1片,进入下轮
- 其他情况 ==> 全部抛弃
递归截止条件:n<=3
3片芯片,一次测试可得到好芯片
1或者2片芯片,不需要再测试,他们都为好芯片。
上述算法过程就是我们给出的分治策略的设计。那么为什么上述的策略是正确的呢?
注意:要保证分治策略的正确性的基本条件是:子问题与原问题性质相同。下面我们就来证明,上述分治策略的子问题与原问题性质相同。
1.41 分治算法的正确性证明
原问题:n片芯片,其中好芯片,至少比坏芯片多一片
那么子问题,命题1:当 n 是偶数时,在上述淘汰规则下,经过一轮淘汰,剩下的好芯片比坏芯片至少多1片
我们需要证明上述子问题的命题1是正确的。
证明:假设原问题中A,B都好的芯片有i组,A与B一好一坏的有j组,A与B都坏的有k组。那么经过一轮淘汰后,好芯片还剩i片,坏芯片还剩k片。
因为
- 初始芯片总数 2i+2j+2k = n
- 初始好芯片多于坏芯片:2i+j > 2k+j
得出:i>k
所以,剩余的芯片好芯片比坏芯片,至少多1片。命题1 是正确的。即证明了上述分治算法的正确性。
当n为奇数时,特殊处理。当n是奇数时,可能会出现问题,如图:
可见淘汰后的子问题并不满足于原问题性质相同,此时无法继续测试。
- 处理办法是:当n为奇数时,增加一轮对轮空芯片的单独测试,如果该轮空芯片为好芯片则算法结束,如果是坏芯片,则淘汰该芯片。
下面给出上述分治算法的伪码描述:

1.42 时间复杂度分析
设输入规模为n,,每轮淘汰后,芯片数至少减半,测试次数(含轮空处理):O(n)
时间复杂度:
W(n) = W(n/2) + O(n)
W(3)=1,W(2)=W(1)=0
主定理求解上述方程的得:W(n) = O(n)
结果很振奋人心,你已经将一个O(n^2)级别的算法优化为了O(n)级别!!!
2. 总结
最大的需要注意的地方就是:如何保证子问题与原问题性质相同:
可以:
1.增加额外处理(比如上述n为奇数时对轮空数据的处理)
2.额外处理的工作量,不改变函数的阶。
参考:北京大学屈婉玲老师公开课
