问题:设有n=2^k个选手参加循环赛,要求设计一个满足以下要求比赛日程表:
1)每个选手必须与其它n-1个选手各赛一次;
2)每个选手一天只能赛一次。
分析,按照上面的要求,可以将比赛表设计成一个n行n-1列的二维表,其中第i行第j列的元素表示和第i个选手在第j天比赛的选手号。
采用分治策略,可将所有参加比赛的选手分成两部分,n=2^k个选手的比赛日程表就可以通过n=2^(k-1)个选手的的比赛日程表来决定。递归的执行这样的分割,直到只剩下两个选手,比赛日程表的就可以通过这样的分治策略逐步构建。
首先看只有两个选手的日程安排,如下图:
解释:如果只有两个选手,那么第0列看作选手编号(我们从0开始对列编号),第1列就是在第一天,每个选手要比赛的选手号。
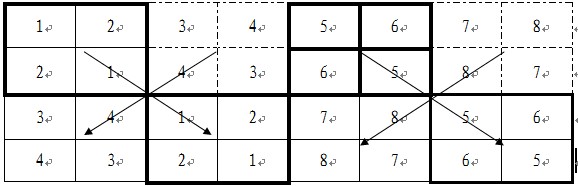
如果选手的个数为2^2=4,那么日程安排如下图
解释:如果有4个选手,分别设计4/2=2个选手的比赛日程表,1-2选手前一天的比赛日程表如上图表格左上角的绿色子表格部分,3-4选手前一天的比赛日程表如上图表格左下角的子表格。据此,后两天的日程表可以将左上角的子表按其对应位置抄到右下角的子表,左下角的子表可以按其对应位置抄到右上角的子表。(同时,我们注意到,这是表的行列均为参赛选手数2^2 = 4,在用分治法求行、列均为(2^2)/2的长度的子表时,首先确定左上角的子表,左下角的子表可以由左上角的子表加(2^2)/2得到)
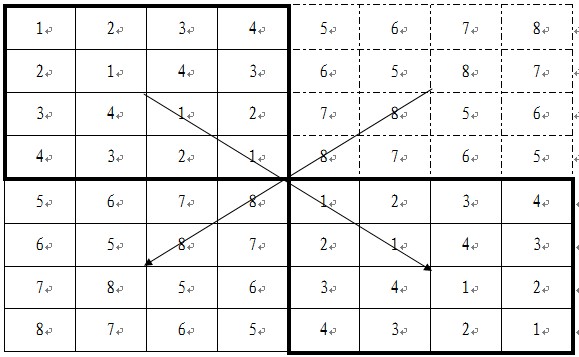
如果选手的个数为2^3=8,那么日程安排表如下:
解释:选手人数为8时,左上角的子表是选手1至选手4的前三天的比赛日程,左下角是选手5至选手8前三天的比赛日程。据此后四天的比赛日程,就是分别将左上角子表按其对应位置抄到右下角,将左下角的子表按其对应位置抄到右上角。这样就完成了比赛日程的安排。
这种解法是把求解2^k个选手的比赛日程问题划分为2^1,2^2,......,2^k个选手的比赛日程问题。也就是说,要求2^k个选手的比赛日程,就要分为两部分,分别求出2^(k-1)个选手的比赛日程,然后再进行合并。当然,这种解法只能求选手个数是2的次幂的情况。
在每次迭代求解的过程中,可以看作4部分:
1)求左上角子表:左上角子表是前2^(k-1)个选手的比赛前半程的比赛日程。
2)求左下角子表:左下角子表是剩余的2^(k-1)个选手的比赛前半程比赛日程。这个子表和左上角子表的对应关系式,对应元素等于左上角子表对应元素加2^(k-1)。
3)求右上角子表:等于左下角子表的对应元素。
4)求右下角子表:等于左上角子表的对应元素。
依据此思想容易将比赛日程表推广到具有任意多个选手情况。
算法步骤:
(1)用一个for循环输出日程表的第一行 for(int i=1;i<=N;i++) a[1][i] = i
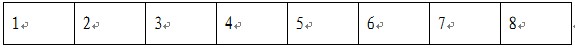
(2)然后定义一个m值,m初始化为1,m用来控制每一次填充表格时i(i表示行)和j(j表示列)的起始填充位置。
(3)用一个for循环将问题分成几部分,对于k=3,n=8,将问题分成3大部分,第一部分为,根据已经填充的第一行,填写第二行,第二部分为,根据已经填充好的第一部分,填写第三四行,第三部分为,根据已经填充好的前四行,填写最后四行。for (ints=1;s<=k;s++) N/=2;
(4)用一个for循环对③中提到的每一部分进行划分for(int t=1;t<=N;t++)对于第一部分,将其划分为四个小的单元,即对第二行进行如下划分

同理,对第二部分(即三四行),划分为两部分,第三部分同理。
(5) 最后,根据以上for循环对整体的划分和分治法的思想,进行每一个单元格的填充。填充原则是:对角线填充
for(int i=m+1;i<=2*m;i++) //i控制行
for(int j=m+1;j<=2*m;j++) //j控制列
{
a[i][j+(t-1)*m*2]= a[i-m][j+(t-1)*m*2-m];/*右下角的值等于左上角的值 */
a[i][j+(t-1)*m*2-m] =a[i-m][j+(t-1)*m*2];/*左下角的值等于右上角的值 */
}
运行过程:
(1)由初始化的第一行填充第二行

(2)由s控制的第一部分填完。然后是s++,进行第二部分的填充
(3)最后是第三部分的填充
程序清单:
#include "stdafx.h"
#include <iostream>
#include <math.h>
using namespace std;
void Table(int k,int n,int **a);
void input(int &k);
void output(int **a,int n);
int main()
{
int k;
input(k);
int n=1;
//n=2k(k>=1)个选手参加比赛
for(int i=1; i<=k; i++)
n *= 2;
//根据n动态分配二维数组a
int **a = new int *[n+1];
for(int i=0;i<=n;i++)
{
a[i] = new int[n+1];
}
Table(k,n,a);
cout<<"循环赛事日程表为:"<<endl;
output(a,n);
//释放空间
for(int i=0;i<=n;i++)
{
delete[] a[i];
}
delete[] a;
return 0;
}
void input(int &k)
{
cout<<"请输入k值:"<<endl;
cin>>k;
}
void output(int **a,int n)
{
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
cout<<a[i][j]<<" ";
}
cout<<endl;
}
}
void Table(int k,int n,int **a)
{
for(int i=1; i<=n; i++)
a[1][i]=i;//设置日程表第一行
int m = 1;//每次填充时,起始填充位置
for(int s=1; s<=k; s++)
{
n /= 2;
for(int t=1; t<=n; t++)
{
for(int i=m+1; i<=2*m; i++)//控制行
{
for(int j=m+1; j<=2*m; j++)//控制列
{
a[i][j+(t-1)*m*2] = a[i-m][j+(t-1)*m*2-m];//右下角等于左上角的值
a[i][j+(t-1)*m*2-m] = a[i-m][j+(t-1)*m*2];//左下角等于右上角的值
}
}
}
m *= 2;
}
}
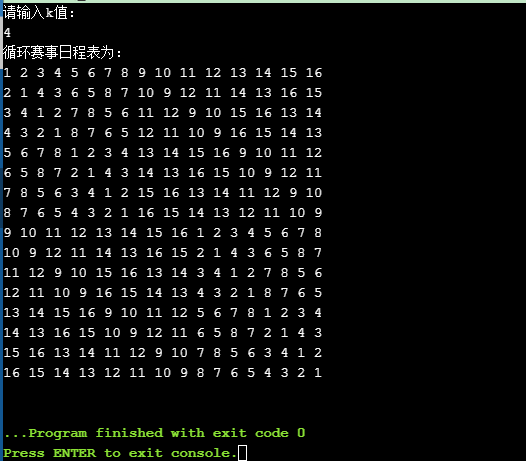
程序运行结果:
参考:https://blog.csdn.net/liufeng_king/article/details/8488421?depth_1-


