投资问题的描述: fi(x)表示的是 把 x 元钱投资到第 i 个项目 所获得的收益。课堂上老师说,约束条件必须满足 投资的钱数 等于总共的钱数

举例说明,更容易理解: 在这个表格中, 比如 坐标 (1,0)对应的值为11,这个含义就是说 把 1 万元投资到项目1中,获得的收益是 11万元。坐标 (3,4)的值为 22, 这个含义就是说 把 3 万元 投资到 项目 4 中,获得的收益是 22万元。

子问题的界定:
k代表的含义是 ,考虑到第几个项目
x代表的含义是: 你投资的钱数不超过 x
所以,这里的 k 和 x 是两个性质不同的参数。
我们之前学的矩阵链相乘, 问题中的 i ,j 是矩阵的下标。是同样类型的参数。
再讨论计算顺序, 先定下 所要投资的项目,是前 k 个,从1,2,3......k
当k 的值确定以后,再让 x 变化。比如,当k的值为5时,我们考虑 x 为1,2,3,4....m 时,获得的收益。

优化函数的递推方程: Fk(x)表示的意思是 把 x 元 投资给 前 k 个项目 获得的最大收益。
x的范围(投资的总的钱数) 是0 到 x
k 的范围是 1 到 n (总共有 n 个项目)
那么 Fk(x) 的值应该是 对 第k个项目投资 了 xk 元 后的收益 + 把剩下的钱(x-xk)投给 前 k-1个项目的总的收益 Fk-1(x-xk)
那么,这个 xk的值 可以从 0 到 x,就是说,可以一分钱也不投资给 第k个项目,也可以把所有钱都投资给 这个项目,所以,这里要遍历 x+1次 才可以获得收益的最大值。

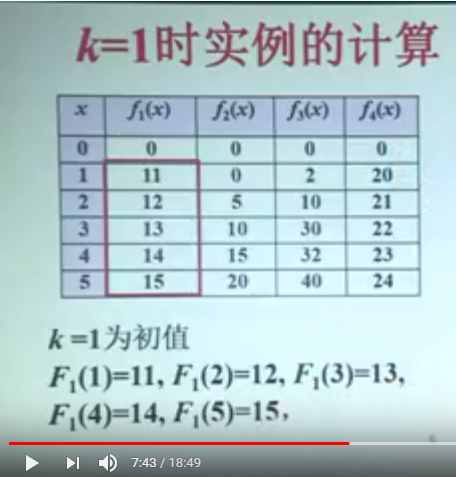
下面举例说明,当 k=1 时, 就是说 考虑前面 第一个 项目。只投资第一个项目。
把 0元投资给第一个项目,收益为0元,
把 1 元投资给第一个项目,收益为 11元
把 2 元投资给第一个项目,收益为 12 元,以此类推
举例说明,当K=2 时, 我们考虑把 钱投资给 前 2 个项目。
K确定以后,我们就要来遍历 x ,x是投资的总的钱数,范围是 从 0 到 5.
当 x= 5时,我们分析情况:
方案有 :(0,5),(5,0),(1,4),(4,1),(2,3),(3,2)
F2( x=5)=max{ f1(0)+f2(5) , f1(5)+f2(0) , f1(1)+f2(4) , f1(4)+f2(1) , f1(2)+f2(3) , f1(3)+f2(2) }
max { 0 +20 , 15+0 , 11 +15 , 14 +0 ,12 + 10 , 13+5 } ,所以,此时最大的收益是 26 万元。

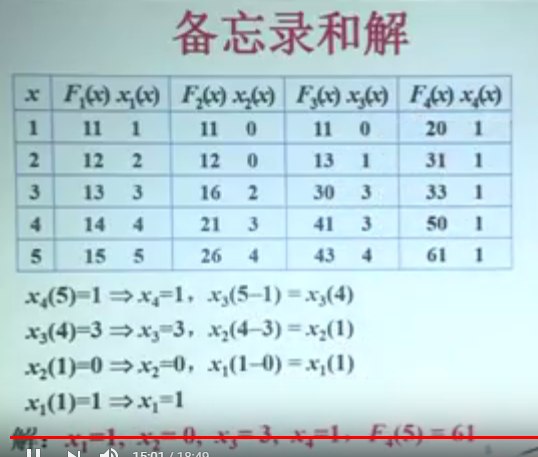
备忘录 和解:
F1(x )就是我们刚刚提到的, 把 x万元投在到 前 k 个项目中,这里 k=1
那么 , x 1(x) 是什么意思呢,这是标记函数, 表示的意思是, 你得到当前的最大收益时,你给了最后一个项目多少钱
比如 ,我们刚刚算的 F 2(5) ,我们把5万元投资到前 2 个项目中, 当获得最大收益 26 万元时, 我 们给第二个项目
投资的是4万元。 上面已经说的很清楚了。
那我们来举个不同的例子分析一下。
比如我要追踪 我投资 4万元给 这四个项目获得的最大收益,显然是 50万元。
此时,给第四个项目的投资是1 万元, x 4( 4)=1, 也就是说, x4=1,d第四个项目投资 1万元
x3(3)= 3, 也就是说,我们把剩余的3 万元全部投资给了 第三个项目
剩下的钱为 0 ,无法投资
时间复杂度分析:
有两种分析方法,



小结:

代码实现:

#include<iostream> #include<vector> using namespace std; int main() { int m, n;//m元钱,n项投资 int i, j;//循环辅助变量 int tmp_m,tmp_F=0;//tem_m代表给第i个项目投入的钱数 0<=tmp<=j;tmp_F代表一次循环中的钱数 cin >> m >> n; vector<vector<int>> f(n, vector<int>(m + 1));//f[i][x], 0<i<=n,0<=x<=m; vector<vector<int>> F(n, vector<int>(m + 1));//F[i][x],将x元钱投入到前i个项目上最大的收益 for (i = 0; i < n; ++i) { f[i][0] = 0;//在第(i+1)个项目上投入0元,收益为0,注意i从0开始 } for (i = 0; i < n; ++i) { for (j = 1; j < m + 1; ++j) {//j从1开始,也就是从f[0][1]开始 cin >> f[i][j]; } } //给F[0][0-m]赋值 for (j = 0; j < m + 1; ++j) { F[0][j] = f[0][j];//第一个项目上投入0-m元钱的最大收益等于f[0][0-m] } for (i = 1; i < n; ++i) {//项目循环,从1开始,也就是从前2个项目开始算,因为第一个项目已经赋值 for (j = 0; j < m + 1; ++j) {//钱数循环 从0开始 for (tmp_m = 0; tmp_m <= j; ++tmp_m) { tmp_F = F[i - 1][j - tmp_m] + f[i][tmp_m]; if (tmp_F > F[i][j]) F[i][j] = tmp_F; } } } cout << "the max profit is : " << F[n - 1][m] << endl; }
实现结果: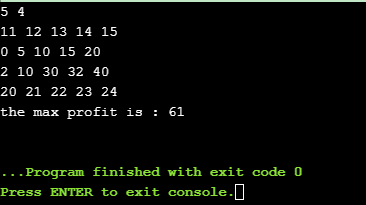
控制台输入说明:
输入:第一行为总钱数m和总项目数n;接下来为n行输入,每行m个,代表f[i][x]。
输出:最大收益。
