贪心法之哈夫曼编码问题

 1、问题描述

      哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，如下表所示。

    有多种方式表示文件中的信息，若用0,1码表示字符的方法，即每个字符用唯一的一个0,1串表示。若采用定长编码表示，则需要3位表示一个字符，整个文件编码需要300,000位；若采用变长编码表示，给频率高的字符较短的编码；频率低的字符较长的编码，达到整体编码减少的目的，则整个文件编码需要（45×1+13×3+12×3+16×3+9×4+5×4）×1000=224,000位，由此可见，变长码比定长码方案好，总码长减小约25%。

     前缀码：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其他字符代码的前缀。这种编码称为前缀码。编码的前缀性质可以使译码方法非常简单；例如001011101可以唯一的分解为0,0,101,1101，因而其译码为aabe。

     译码过程需要方便的取出编码的前缀，因此需要表示前缀码的合适的数据结构。为此，可以用二叉树作为前缀码的数据结构：树叶表示给定字符；从树根到树叶的路径当作该字符的前缀码；代码中每一位的0或1分别作为指示某节点到左儿子或右儿子的“路标”。

     从上图可以看出，表示最优前缀码的二叉树总是一棵完全二叉树，即树中任意节点都有2个儿子。图a表示定长编码方案不是最优的，其编码的二叉树不是一棵完全二叉树。在一般情况下，若C是编码字符集，表示其最优前缀码的二叉树中恰有|C|个叶子。每个叶子对应于字符集中的一个字符，该二叉树有|C|-1个内部节点。

     给定编码字符集C及频率分布f,即C中任一字符c以频率f(c)在数据文件中出现。C的一个前缀码编码方案对应于一棵二叉树T。字符c在树T中的深度记为dT(c)。dT(c)也是字符c的前缀码长。则平均码长定义为：使平均码长达到最小的前缀码编码方案称为C的最优前缀码。     

     2、构造哈弗曼编码

     哈夫曼提出构造最优前缀码的贪心算法，由此产生的编码方案称为哈夫曼编码。其构造步骤如下：

     (1)哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。

     (2)算法以|C|个叶结点开始，执行|C|－1次的“合并”运算后产生最终所要求的树T。

     (3)假设编码字符集中每一字符c的频率是f(c)。以f为键值的优先队列Q用在贪心选择时有效地确定算法当前要合并的2棵具有最小频率的树。一旦2棵具有最小频率的树合并后，产生一棵新的树，其频率为合并的2棵树的频率之和，并将新树插入优先队列Q。经过n－1次的合并后，优先队列中只剩下一棵树，即所要求的树T。

      构造过程如图所示：

     具体代码实现如下：

(1)4d4.cpp，程序主文件

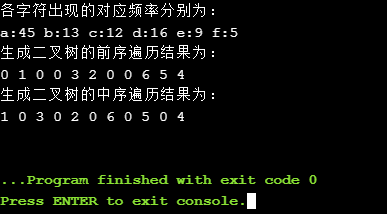
//4d4 贪心算法 哈夫曼算法
#include "stdafx.h"
#include "BinaryTree.h"
#include "MinHeap.h"
#include <iostream> 
using namespace std; 
 
const int N = 6;
 
template<class Type> class Huffman;
 
template<class Type> 
BinaryTree<int> HuffmanTree(Type f[],int n);
 
template<class Type> 
class Huffman
{
    friend BinaryTree<int> HuffmanTree(Type[],int);
    public:
        operator Type() const 
        {
            return weight;
        }
    //private:
        BinaryTree<int> tree;
        Type weight;
};
 
int main()
{
    char c[] = {'0','a','b','c','d','e','f'};
    int f[] = {0,45,13,12,16,9,5};//下标从1开始
    BinaryTree<int> t = HuffmanTree(f,N);
 
    cout<<"各字符出现的对应频率分别为："<<endl;
    for(int i=1; i<=N; i++)
    {
        cout<<c[i]<<":"<<f[i]<<" ";
    }
    cout<<endl;
 
    cout<<"生成二叉树的前序遍历结果为："<<endl;
    t.Pre_Order();
    cout<<endl;
 
    cout<<"生成二叉树的中序遍历结果为："<<endl;
    t.In_Order();
    cout<<endl;
 
    t.DestroyTree();
    return 0;
}
 
template<class Type>
BinaryTree<int> HuffmanTree(Type f[],int n)
{
    //生成单节点树
    Huffman<Type> *w = new Huffman<Type>[n+1];
    BinaryTree<int> z,zero;
 
    for(int i=1; i<=n; i++)
    {
        z.MakeTree(i,zero,zero);
        w[i].weight = f[i];
        w[i].tree = z;
    }
 
    //建优先队列
    MinHeap<Huffman<Type>> Q(n);
    for(int i=1; i<=n; i++) Q.Insert(w[i]);
 
    //反复合并最小频率树
    Huffman<Type> x,y;
    for(int i=1; i<n; i++)
    {
        x = Q.RemoveMin();
        y = Q.RemoveMin();
        z.MakeTree(0,x.tree,y.tree);
        x.weight += y.weight;
        x.tree = z;
        Q.Insert(x);
    }
 
    x = Q.RemoveMin();
 
    delete[] w;
 
    return x.tree;
}

  (2)BinaryTree.h 二叉树实现

#include<iostream>
using namespace std;
 
template<class T>
struct BTNode
{
    T data;
    BTNode<T> *lChild,*rChild;
 
    BTNode()
    {
        lChild=rChild=NULL;
    }
 
    BTNode(const T &val,BTNode<T> *Childl=NULL,BTNode<T> *Childr=NULL)
    {
        data=val;
        lChild=Childl;
        rChild=Childr;
    }
 
    BTNode<T>* CopyTree()
    {
        BTNode<T> *nl,*nr,*nn;
 
        if(&data==NULL)
        return NULL;
 
        nl=lChild->CopyTree();
        nr=rChild->CopyTree();
 
        nn=new BTNode<T>(data,nl,nr);
        return nn;
    }
};
 
 
template<class T>
class BinaryTree
{
    public:
        BTNode<T> *root;
        BinaryTree();
        ~BinaryTree();
 
        void Pre_Order();
        void In_Order();
        void Post_Order();
 
        int TreeHeight()const;
        int TreeNodeCount()const;
 
        void DestroyTree();
        void MakeTree(T pData,BinaryTree<T> leftTree,BinaryTree<T> rightTree);
        void Change(BTNode<T> *r);
 
    private:
        void Destroy(BTNode<T> *&r);
        void PreOrder(BTNode<T> *r);
        void InOrder(BTNode<T> *r);
        void PostOrder(BTNode<T> *r);
 
        int Height(const BTNode<T> *r)const;
        int NodeCount(const BTNode<T> *r)const;
};
 
template<class T>
BinaryTree<T>::BinaryTree()
{
    root=NULL;
}
 
template<class T>
BinaryTree<T>::~BinaryTree()
{
    
}
 
template<class T>
void BinaryTree<T>::Pre_Order()
{
    PreOrder(root);
}
 
template<class T>
void BinaryTree<T>::In_Order()
{
    InOrder(root);
}
 
template<class T>
void BinaryTree<T>::Post_Order()
{
    PostOrder(root);
}
 
template<class T>
int BinaryTree<T>::TreeHeight()const
{
    return Height(root);
}
 
template<class T>
int BinaryTree<T>::TreeNodeCount()const
{
    return NodeCount(root);
}
 
template<class T>
void BinaryTree<T>::DestroyTree()
{
    Destroy(root);
}
 
template<class T>
void BinaryTree<T>::PreOrder(BTNode<T> *r)
{
    if(r!=NULL)
    {
        cout<<r->data<<' ';
        PreOrder(r->lChild);
        PreOrder(r->rChild);
    }
}
 
template<class T>
void BinaryTree<T>::InOrder(BTNode<T> *r)
{
    if(r!=NULL)
    {
        InOrder(r->lChild);
        cout<<r->data<<' ';
        InOrder(r->rChild);
    }
}
 
template<class T>
void BinaryTree<T>::PostOrder(BTNode<T> *r)
{
    if(r!=NULL)
    {
        PostOrder(r->lChild);
        PostOrder(r->rChild);
        cout<<r->data<<' ';
    }
}
 
template<class T>
int BinaryTree<T>::NodeCount(const BTNode<T> *r)const
{
    if(r==NULL)
        return 0;
    else
        return 1+NodeCount(r->lChild)+NodeCount(r->rChild);
}
 
template<class T>
int BinaryTree<T>::Height(const BTNode<T> *r)const
{
    if(r==NULL)
        return 0;
    else
    {
        int lh,rh;
        lh=Height(r->lChild);
        rh=Height(r->rChild);
        return 1+(lh>rh?lh:rh);
    }
}
 
template<class T>
void BinaryTree<T>::Destroy(BTNode<T> *&r)
{
    if(r!=NULL)
    {
        Destroy(r->lChild);
        Destroy(r->rChild);
        delete r;
        r=NULL;
    }
}
 
template<class T>
void BinaryTree<T>::Change(BTNode<T> *r)//将二叉树bt所有结点的左右子树交换
{
    BTNode<T> *p;
    if(r){ 
        p=r->lChild;
        r->lChild=r->rChild;
        r->rChild=p; //左右子女交换
        Change(r->lChild);  //交换左子树上所有结点的左右子树
        Change(r->rChild);  //交换右子树上所有结点的左右子树
    }
}
 
template<class T>
void BinaryTree<T>::MakeTree(T pData,BinaryTree<T> leftTree,BinaryTree<T> rightTree)
{
    root = new BTNode<T>();
    root->data = pData;
    root->lChild = leftTree.root;
    root->rChild = rightTree.root;
}

(3)MinHeap.h 最小堆实现

#include <iostream>
using namespace std;
template<class T>
class MinHeap
{
    private:
        T *heap; //元素数组，0号位置也储存元素
        int CurrentSize; //目前元素个数
        int MaxSize; //可容纳的最多元素个数
 
        void FilterDown(const int start,const int end); //自上往下调整，使关键字小的节点在上
        void FilterUp(int start); //自下往上调整
 
    public:
        MinHeap(int n=1000);
        ~MinHeap();
        bool Insert(const T &x); //插入元素
 
        T RemoveMin(); //删除最小元素
        T GetMin(); //取最小元素
 
        bool IsEmpty() const;
        bool IsFull() const;
        void Clear();
};
 
template<class T>
MinHeap<T>::MinHeap(int n)
{
    MaxSize=n;
    heap=new T[MaxSize];
    CurrentSize=0;
}
 
template<class T>
MinHeap<T>::~MinHeap()
{
    delete []heap;
}
 
template<class T>
void MinHeap<T>::FilterUp(int start) //自下往上调整
{
    int j=start,i=(j-1)/2; //i指向j的双亲节点
    T temp=heap[j];
 
    while(j>0)
    {
        if(heap[i]<=temp)
            break;
        else
        {
            heap[j]=heap[i];
            j=i;
            i=(i-1)/2;
        }
    }
    heap[j]=temp;
}
 
template<class T>
void MinHeap<T>::FilterDown(const int start,const int end) //自上往下调整，使关键字小的节点在上
{
    int i=start,j=2*i+1;
    T temp=heap[i];
    while(j<=end)
    {
        if( (j<end) && (heap[j]>heap[j+1]) )
            j++;
        if(temp<=heap[j])
            break;
        else
        {
            heap[i]=heap[j];
            i=j;
            j=2*j+1;
        }
    }
    heap[i]=temp;
}
 
template<class T>
bool MinHeap<T>::Insert(const T &x)
{
    if(CurrentSize==MaxSize)
        return false;
 
    heap[CurrentSize]=x;
    FilterUp(CurrentSize);
 
    CurrentSize++;
    return true;
}
 
template<class T>
T MinHeap<T>::RemoveMin( )
{
    T x=heap[0];
    heap[0]=heap[CurrentSize-1];
 
    CurrentSize--;
    FilterDown(0,CurrentSize-1); //调整新的根节点
 
    return x;
}
 
template<class T>
T MinHeap<T>::GetMin()
{
    return heap[0];
}
 
template<class T>
bool MinHeap<T>::IsEmpty() const
{
    return CurrentSize==0;
}
 
template<class T>
bool MinHeap<T>::IsFull() const
{
    return CurrentSize==MaxSize;
}
 
template<class T>
void MinHeap<T>::Clear()
{
    CurrentSize=0;
}

 3、贪心选择性质

证明哈夫曼算法正确性的两个引理

 

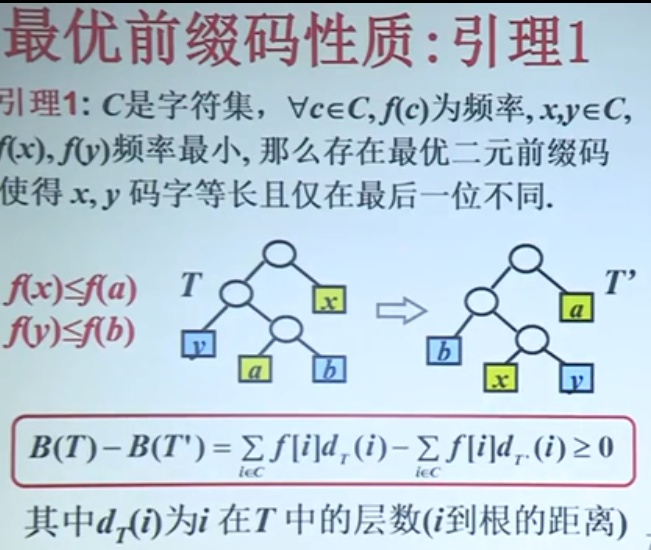
     二叉树T表示字符集C的一个最优前缀码，证明可以对T作适当修改后得到一棵新的二叉树T”，在T”中x和y是最深叶子且为兄弟，同时T”表示的前缀码也是C的最优前缀码。设b和c是二叉树T的最深叶子，且为兄弟。设f(b)<=f(c)，f(x)<=f(y)。由于x和y是C中具有最小频率的两个字符，有f(x)<=f(b)，f(y)<=f(c)。首先，在树T中交换叶子b和x的位置得到T'，然后再树T'中交换叶子c和y的位置，得到树T''。如图所示：

    由此可知，树T和T'的前缀码的平均码长之差为：

     因此，T''表示的前缀码也是最优前缀码，且x,y具有相同的码长，同时，仅最优一位编码不同。

     4、最优子结构性质

     二叉树T表示字符集C的一个最优前缀码，x和y是树T中的两个叶子且为兄弟，z是它们的父亲。若将z当作是具有频率f(z)=f(x)+f(y)的字符，则树T’=T-{x,y}表示字符集C’=C-{x, y} ∪ { z}的一个最优前缀码。因此，有：

如果T’不是C’的最优前缀码，假定T”是C’的最优前缀码，那么有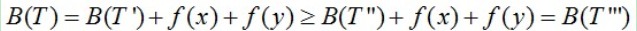，显然T”’是比T更优的前缀码，跟前提矛盾！故T'所表示的C'的前缀码是最优的。

     由贪心选择性质和最优子结构性质可以推出哈夫曼算法是正确的，即HuffmanTree产生的一棵最优前缀编码树。

     程序运行结果如图：

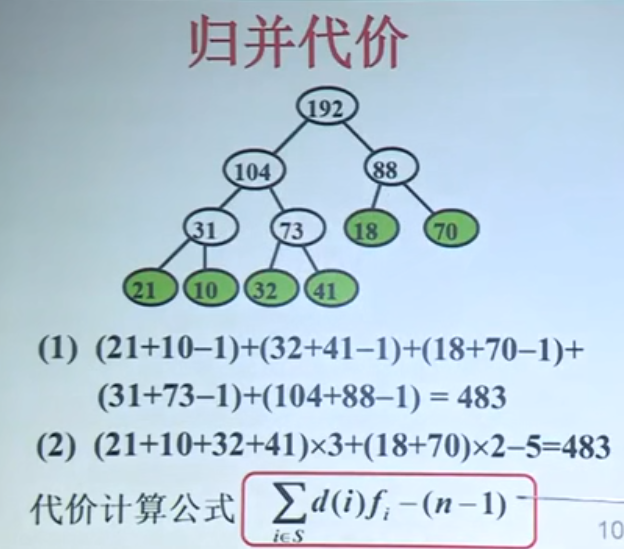
5.哈夫曼算法应用

 

 

 

 参考：北大《算法设计与分析》公开课         

            王晓东《算法设计与分析》

            CSDN:https://blog.csdn.net/liufeng_king/article/details/8720896