主席树
(看dalao们都写博客,我一个蒟蒻来凑个热闹)
主席树看了1D,终于大致领悟了(^.^)
首先我们来了解什么叫做主席树,下面是从其他大佬的博客中复制过来的了解一下就行
所谓主席树呢,就是对原来的数列[1..n]的每一个前缀[1..i](1≤i≤n)建立一棵线段树(至于为什么要是前缀往下看...),线段树的每一个节点存某个前缀[1..i]中属于区间[L..R]的数一共有多少个(比如根节点是[1..n],一共i个数,sum[root] = i;根节点的左儿子是[1..(L+R)/2],若不大于(L+R)/2的数有x个,那么sum[root.left] = x)。若要查找[i..j]中第k大数时,设某结点x,那么x.sum[j] - x.sum[i - 1]就是[i..j]中在结点x内的数字总数。而对每一个前缀都建一棵树,会MLE,观察到每个[1..i]和[1..i-1]只有一条路是不一样的,那么其他的结点只要用回前一棵树的结点即可,时空复杂度为O(nlogn)。
---------------------
是不是看的一脸懵逼,下面我就给大家翻译一下这段话。
想学会主席树就要先学好线段树,因为主席树的本质就是多颗线段树串起来。线段树在此就不多说了。
想要求区间的第k小,当然与当然与这个区间有多少数比他小有关,在这里我举一个例子来说明一下怎样建立这样的一颗线段树。比如一个数列的某个区间表示的序列是4,1,3,2,我们要求第2小,下面我画了一幅图来讲解,其中这颗线段树上的每个节点维护的是这个节点表示区间内的个数(比较丑,大家将就一下哈)。
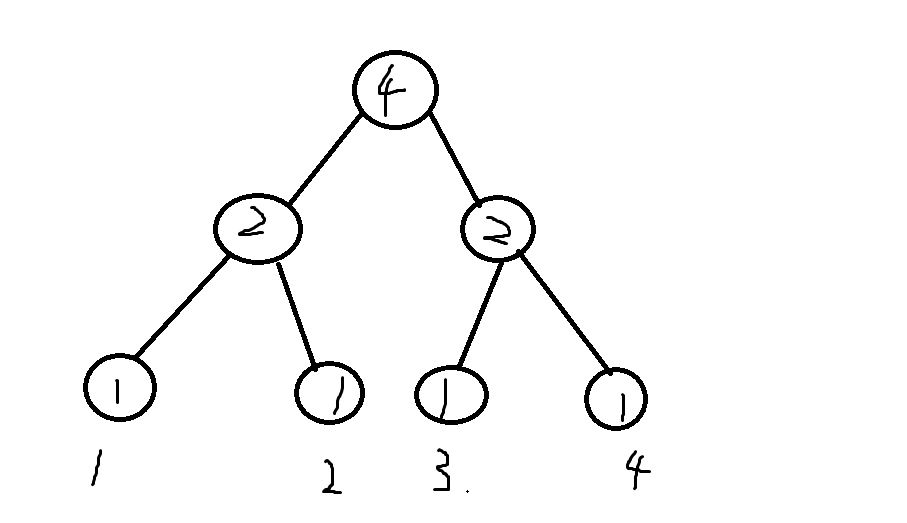
圈内的数字表示这个区间里面有多少个数,最后叶节点表示一个数字,对应上述序列中的一个数(因为每个数a[i]都在1e9内,而n只小于1e5,所以我们可以离散一下)。这样的话,想要找第k小的,先找左儿子节点,如果左儿子的叶子结点数多于k,那么第k大的数就在左儿子的叶子结点里面。否则就在右儿子里面。一直找到叶子结点,返回节点上的数就可以了。
但多次询问区间的第k小,每次询问都建一棵树一定会TLE的,这样的话就使ta有了巨大的局限性,怎样优化一下呢?又废话了
我们很容易就联想到了前缀和的概念,比如我们有一个问题。就是每次静态的求区间和,我们可以预处理所以的前缀和sum[i],我们每次求解区间l, r和时,我们可以直接得到答案为sum[r] - sum[l-1],这样就不需要对区间中的每个数进行相加来求解了。
同样一个道理,我们也可以利用前缀和这个思想来解决建树这个问题,我们只需要建立n颗前缀线段树就行,第i树维护[1,i]序列,这样我们处理任意区间l, r时就可以通过处理区间[1,l - 1], [1,r],就行,然后两者的处理结果进行相加相减就行。为什么满足相加减的性质,我们简单分析一下就很容易得出。如果在区间[1,l-1]中有x个数小于一个数p,在[1,r]中有y个数小于p,那么在区间[l,r]中就有y - x 个数小于p,这样就很好理解为什么可以相加减了,而我们的主席树就是在已知y-x时用二分法来找p是多少。是不是理解一点了。
若是每个点都建一颗数的话还是会MLE的,怎么办呢?
例:有一个这样的数列
5
4 2 5 3 1
以第一个数为根:
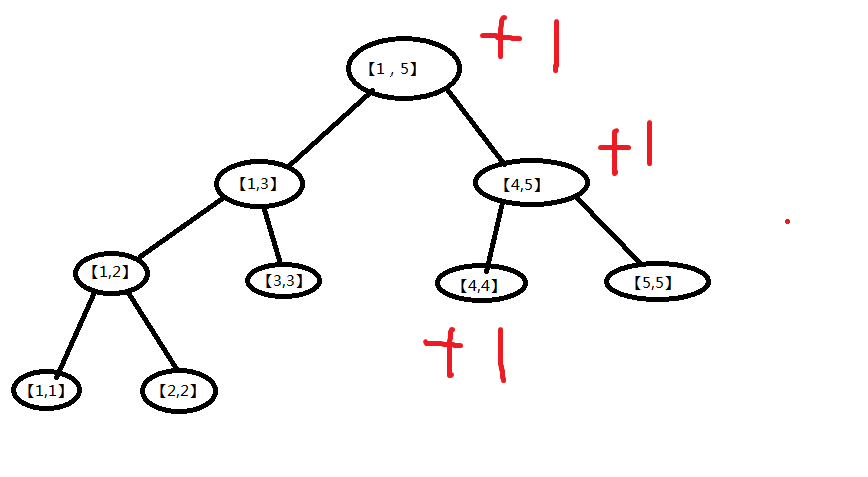
以第二个数为根:
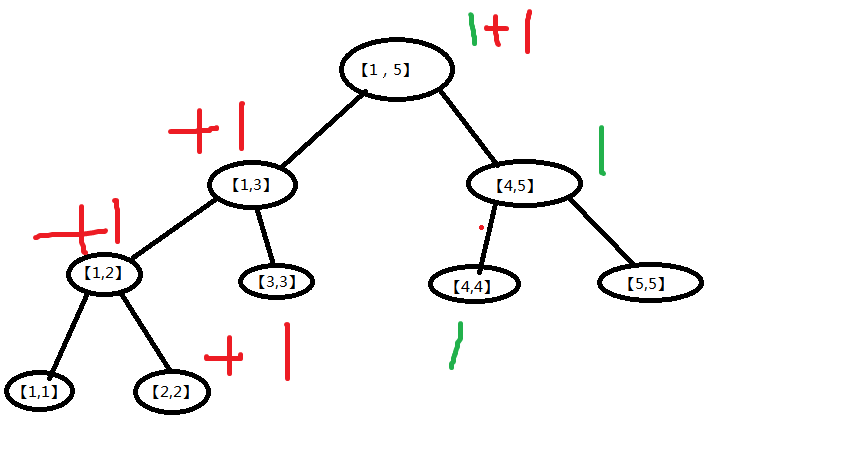
我们会发现只有4个点各加了1,其他点都没变。所以我们就可以让两颗树共用这些没变的点:
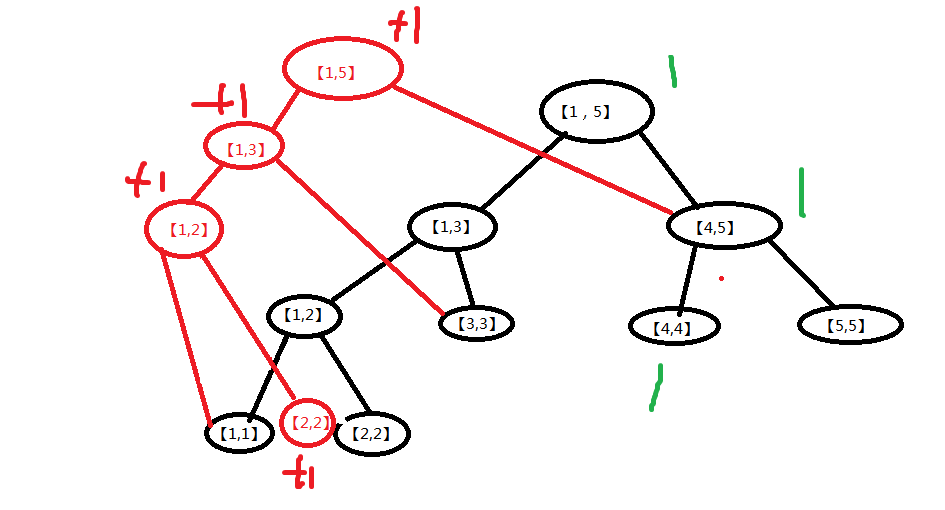
红色是新增的点,这样的话就只需多开4个点就可以了,是不是很省空间。后面的点依次累加上就好了。(图我就不画了哈,太大了(^-^))
那么我们就是可以保证是没有问题,而且时间与空间复杂度都是稳定的树了
上代码

1 //主席树
2 #include<bits/stdc++.h>
3 using namespace std;
4 #define ll long long
5 #define C continue
6 #define B break
7 #define N 200100
8 inline int read()//快读不解释
9 {
10 int f=1,x=0;
11 char ch=getchar();
12 while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
13 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
14 return x*f;
15 }
16 int n,m,ql,qr,a[N],b[N],rs[N*25],ls[N*25],rt[N*25],kk,d[N*25],sz,t=0;//d表示这颗子数里插入多少数了。
17 void build(int &o, int l, int r)//先在0号点建一棵树
18 {
19 o=++t;
20 d[o]=0;
21 if(l==r) return ;
22 int mid = (l + r) >>1;
23 build(ls[o],l,mid);
24 build(rs[o],mid+1,r);
25 }
26 void update(int &o,int l,int r,int la,int p) //插入一个点
27 {
28 o=++t;
29 ls[o]=ls[la];
30 rs[o]=rs[la];
31 d[o]=d[la]+1;
32 if(l==r) return ;
33 int mid=(l+r)>>1;
34 if(p<=mid)update(ls[o],l,mid,ls[la],p);
35 else update(rs[o],mid+1,r,rs[la],p);
36 }
37 int query(int s,int e,int l,int r,int k) //查询
38 {
39 if(l==r) return l;
40 int an=d[ls[e]]-d[ls[s]];
41 int mid=(l+r)>>1;
42 if(k<=an) return query(ls[s],ls[e],l,mid,k);
43 else return query(rs[s],rs[e],mid+1,r,k-an);
44 }
45 int main()
46 {
47 n=read();m=read();t=0;
48 for(int i=1;i<=n;i++) a[i]=read(),b[i]=a[i];
49 sort(b+1,b+n+1);
50 sz=unique(b+1,b+n+1)-(b+1); //离散化不解释
51 build(rt[0],1,sz);
52 for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+sz+1,a[i])-b;
53 for(int i=1;i<=n;i++) update(rt[i],1,sz,rt[i-1],a[i]);
54 while(m--)
55 {
56 ql=read();qr=read();kk=read();
57 int ans=query(rt[ql-1],rt[qr],1,sz,kk);
58 printf("%d
",b[ans]);
59 }
60 return 0;
61 }
-------------------------------------------------------------------------------------------------------------------------------------------
小结:(自己的一点总结,欢迎大家评论)
做了几道主席树的题后,感觉主席树其实有点像高级的多个桶排,每颗线段树都是一个桶排数组,每个叶子结点就相当于桶排数组里的一个数。总共 n 个桶排数组,每个数组记录前i个数的桶排。对于桶排,想求区间[l,r]的小于k的数的累加和,就是把前 r 个数的桶排中小于 k 的数的累加和减去前 l-1 个数的桶排中小于 k 的数的累加和(小于k的什么什么什么(可以是数的个数,也可以是数的值)的累加和很好求,因为桶排数组是有序的)大家感性理解一下。把每个叶子结点想象成桶排中的一个数,而节点就是ta所对应的区间[L,R]的什么什么什么的累加和,就是L<=x[i]<=R的什么什么什么的累加和。
至于为什么不直接用多个桶排写这类题,应该是会MLE吧,毕竟要开n个长度为n的数组,而n总是<=1e5的。为什么主席树不会爆空间,大家往上翻。
自我感觉主席树最重要的操作就是求[l,r]内数值范围在[L,R]的什么什么什么的累加和。
