方法一:枚举法。该方法是最容易、也是最简单的方法,枚举出数组A和数组B中所有的元素对,判断其和是否为c,如果是,则输出。
方法二:排序+二分查找法。首先,对两个数组中长度较大数组,不妨设为A,排序;然后,对于B中每个元素B[i]在A中二分查找c-B[i],如果找到,直接输出。
方法三:排序+线性扫描法。首先,对A和B进行排序;然后用指针p从头扫描A,用指针q从尾扫描B,如果A[p]+B[q]==c,则输出A[p]+B[q],且p++,q--;如果A[p]+B[q]>c,则q--;否则p++。
代码如下:
#include "stdafx.h"
#include <stdio.h>
void sortArray(int a[], int n)
{
if (a == NULL || n <= 0)
printf("数组中无元素,排个毛啊。");
else
{
int temp;
for (int i = 0; i < n-1; i++)
{
for (int j = i + 1; j < n; j++)
{
if (a[i]>a[j])
{
a[i] = a[i] ^ a[j];
a[j] = a[j] ^ a[i];
a[i] = a[i] ^ a[j];
}
}
}
}
}
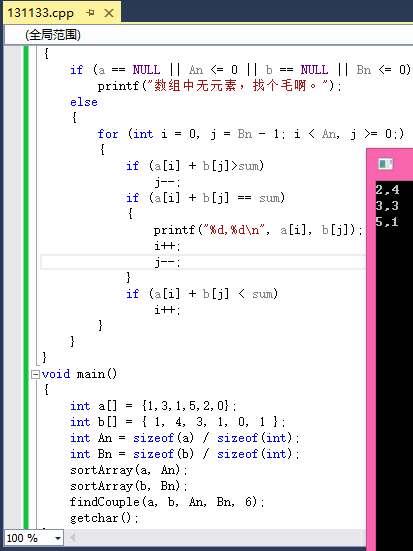
void findCouple(int a[], int b[], int An, int Bn,int sum)
{
if (a == NULL || An <= 0 || b == NULL || Bn <= 0)
printf("数组中无元素,找个毛啊。");
else
{
for (int i = 0, j = Bn - 1; i < An, j >= 0;)
{
if (a[i] + b[j]>sum)
j--;
if (a[i] + b[j] == sum)
{
printf("%d,%d
", a[i], b[j]);
i++;
j--;
}
if (a[i] + b[j] < sum)
i++;
}
}
}
void main()
{
int a[] = {1,3,1,5,2,0};
int b[] = { 1, 4, 3, 1, 0, 1 };
int An = sizeof(a) / sizeof(int);
int Bn = sizeof(b) / sizeof(int);
sortArray(a, An);
sortArray(b, Bn);
findCouple(a, b, An, Bn, 6);
getchar();
}
效果如图:
方法四:Hash法。首先,将两个数组中长度较小的数组,不妨设为A,保存到哈希表中,然后,对于B中每个元素B[i],也采用相同的hash算法在哈希表中查找c-B[i]是否存在,如果存在,则输出.时间复杂度为O(m+n),空间复杂度为O(min{m,n})。但这种算法有个问题,就是会出现重复。
代码如下:
#include "stdafx.h"
#include <iostream>
#include <map>
using namespace std;
void print_pairs_with_sum2(int A[], int B[], int m, int n, int sum)
{
map<int, bool> hash_table;
int *psmaller = A;
int *pbigger = B;
int nsmaller = (m >= n) ? n : m;
int nbigger = (m >= n) ? m : n;
if (m > n)
{
psmaller = B;
pbigger = A;
}
for (int i = 0; i < nsmaller; i++)
{
hash_table.insert(pair<int, bool>(psmaller[i], true));
}
for (int i = 0; i < nbigger; i++)
{
if (hash_table.find(sum - pbigger[i])!= hash_table.end())
{
cout << "(" << pbigger[i] << "," << sum - pbigger[i] << ")" << endl;
}
}
}
void main()
{
int a[] = { 1, 5, 4, 3, 2, 0 };
int b[] = { 1, 4, 3, 1, 0, 1 ,};
int m = sizeof(a) / sizeof(int);
int n = sizeof(b) / sizeof(int);
print_pairs_with_sum2(a, b, m, n, 6);
getchar();
}
效果如图:
