堆与堆排序
堆
定义:堆是一颗完全二叉树,且满足子结点不大于父节点或不小于父节点,即小根堆和大根堆。堆的每一棵子树也都是一个堆。
下图为一个大根堆。
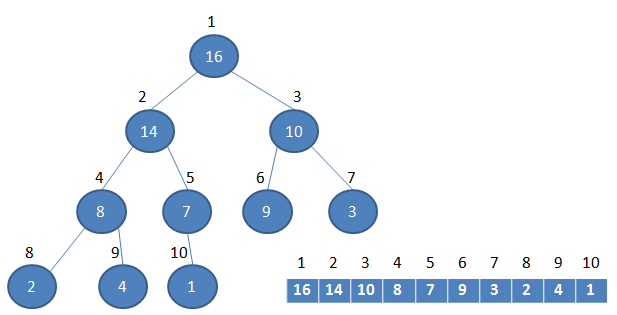
基本操作:最基本的操作包括插入(insert),向上调整(up),删除(delete),向下调整(down),查询(quary)。
插入insert:
给定你一个元素以后将其插入已有的堆中,直接放在堆的末端,再向上调整即可。
Code:
inline void up(int ka) { while(ka>1) { if(heap[ka]<heap[ka/2]) { swap(heap[ka],heap[ka/2]); ka/=2; } else break; } } inline void insert(int x) { heap[++size]=x; up(size); }
删除delete:
一般是将堆顶元素删除,直接将堆末端的元素放到堆顶,再将堆的size--,然后想下调整就可以了。
Code:
inline void down(int ka) { int s=ka*2; while(s<=size) { if(s<size&&heap[s+1]<heap[s]) s++; if(heap[ka]>heap[s]) { swap(heap[ka],heap[s]); ka=s;s=ka*2; } else break; } } inline void erase() { heap[1]=heap[size--]; down(1); }
查询quary:
直接输出堆顶元素即可,没什么好讲的。
堆排序
部分转载自https://www.cnblogs.com/chengxiao/p/6129630.html,转载请注明出处
堆排序是利用堆的性质来进行数据排序的排序方法。堆排序属于选择排序,是不稳定的排序,最坏、最好、平均时间复杂度均为O(nlogn)。
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
a.假设给定无序序列结构如下

2.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。

4.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。

这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。

此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构,使其继续满足堆定义

c.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.

后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
几道题(mu)目(ban)
Luogu.org P1090 合并果子
Luogu.org P1168 中位数
Luogu.org P2085 最小函数值
Luogu.org P1801 黑匣子