Evanyou Blog 彩带

　　题目传送门

电路维修

题目背景

Elf 是来自Gliese 星球的少女，由于偶然的原因漂流到了地球上。在她无依无靠的时候，善良的运输队员Mark 和James 收留了她。Elf 很感谢Mark和James，可是一直也没能给他们帮上什么忙。

题目描述

有一天 Mark 和James 的飞行车没有办法启动了，经过检查发现原来是电路板的故障。飞行车的电路板设计很奇葩，如下图所示：

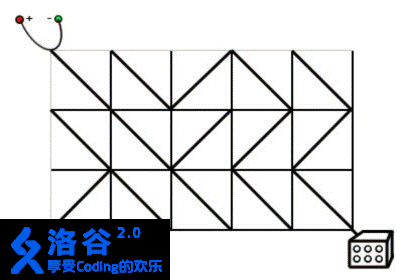
输入输出格式

输入格式：

 

输入文件包含多组测试数据。第一行包含一个整数T 表示测试数据的数目。

对于每组测试数据，第一行包含正整数 R 和C，表示电路板的行数和列数。

之后 R 行，每行C 个字符，字符是"/"和""中的一个，表示标准件的方向。

对于40% 的数据，R,C≤5。

对于 100% 的数据，R,C≤500，T≤5。

 

输出格式：

 

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出 NO SOLUTION。

 

输入输出样例

输入样例#1： 

1
3 5
\/\
\///
/\\

输出样例#1： 

1

说明

样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

---

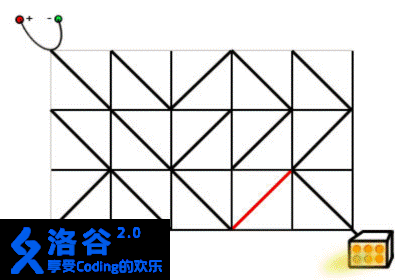
　　分析：

　　一开始看到这题还是被吓了一下，一堆斜杠什么的真的头疼。。

　　但是如果转换一下思维就很容易了，我们把格子中的每一个交点作为图的节点，电路就是边，那么不难想到，一个格子周围有四个点，一条电路会联通其中两个，另外两个如果需要联通就需要转一次。那么就可以把这条信息转化为边权，建图然后跑最短路就行了。

　　蒟蒻不会堆优化的Dijkstra，就索性打了个spfa然后开O2强行A了23333。得去补一下堆优化Dijkstra了。。。

　　Code：

//It is made by HolseLee on 7th Aug 2018
//Luogu.org P2243
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<queue>
using namespace std;

const int N=505;
const int inf=2e9+7;
int n,m,T,dis[N*N],head[N*N],size;
char ch[N];
bool vis[N*N];
struct Node{
    int to,next,val;
}edge[(N*N)<<2];
queue<int>team;

inline int read()
{
    char ch=getchar();int num=0;bool flag=false;
    while(ch<'0'||ch>'9'){if(ch=='-')flag=true;ch=getchar();}
    while(ch>='0'&&ch<='9'){num=num*10+ch-'0';ch=getchar();}
    return flag?-num:num;
}

inline void add(int x,int y,int z)
{
    edge[++size].to=y;
    edge[size].val=z;
    edge[size].next=head[x];
    head[x]=size;
}

void spfa()
{
    while(!team.empty())team.pop();
    memset(vis,false,sizeof(vis));
    memset(dis,0x7f,sizeof(dis));
    team.push(1);
    vis[1]=true;dis[1]=0;
    int x,y;
    while(!team.empty()){
        x=team.front();team.pop();
        vis[x]=false;
        for(int i=head[x];i!=-1;i=edge[i].next){
            y=edge[i].to;
            if(dis[y]>dis[x]+edge[i].val){
                dis[y]=dis[x]+edge[i].val;
                if(!vis[y])team.push(y),vis[y]=true;
            }
        }
    }
}

int main()
{
    T=read();
    while(T--){
        n=read();m=read();
        size=0;
        memset(head,-1,sizeof(head));
        int lu,ru,ld,rd;
        for(int i=1;i<=n;++i){
            scanf("%s",ch+1);
            for(int j=1;j<=m;++j){
                lu=((i-1)*(m+1)+j);
                ru=((i-1)*(m+1)+j+1);
                ld=(i*(m+1)+j);
                rd=(i*(m+1)+j+1);
                if(ch[j]=='/'){
                    add(lu,rd,1);
                    add(rd,lu,1);
                    add(ld,ru,0);
                    add(ru,ld,0);
                }
                else {
                    add(lu,rd,0);
                    add(rd,lu,0);
                    add(ld,ru,1);
                    add(ru,ld,1);
                }
            }
        }
        spfa();
        if(dis[(n+1)*(m+1)]>inf)
            printf("NO SOLUTION
");
        else 
            printf("%d
",dis[(n+1)*(m+1)]);
    }
    return 0;
}