可并堆$(Mergeable Heap)$是一类抽象数据类型,它除了支持一般的优先队列的基本操作以外,还支持额外的合并操作。而可并堆有多种,包括斜堆,左偏树,二项堆,配对堆,斐波那契堆等。
这里我们只介绍左偏树($Leftist Tree$),它是最常用的一种可并堆。至于为什么说最常用,我们会在后面讲到。(先挖个坑)
讲的可能不太好还请包涵,如果有错也希望能及时指出,也欢迎大家在评论区讨论。
本文同步发表在博主的洛谷博客里。
感谢洛谷的巨佬Planet6174提供的图片。
定义
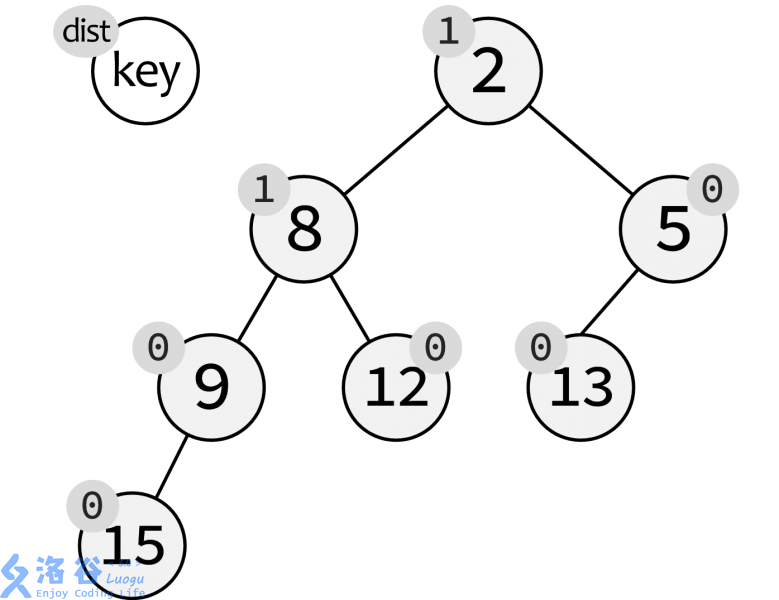
左偏树是一种具有左偏性质的堆有序二叉树(这里要注意,堆有序二叉树和二叉堆并不是同一种东西,因此左偏树并不是堆)。每一个节点存储的信息包括左右子节点、关键值以及距离(当然也有很多时候我们需要维护父节点)。
节点的距离可以这样定义:
某个节点被称为外节点,仅当这个节点的左子树或右子树为空。某一个节点的距离即该节点到与其最近的外节点经过的边数。易得,外节点的距离为$0$,空节点距离为$-1$。特别的,我们把根结点的距离称为这棵左偏树的距离。
下图为一棵左偏树:
基本性质及引理
首先说明,下文中的$val$表示节点的键值,$dist$表示节点的距离。
性质1:
堆的性质,即对于任意节点$p$,$val[p]geq$(或$leq$) $val[lson],val[rson]$。
性质2:
$dist[lson]geq dist[rson]$,即左子树距离一定大于等于右子树距离。
左偏树,顾名思义,就是向左偏的树,就是这个性质在图像可视化后的诠释。
这个性质的存在主要是为了保证左偏树的复杂度,因为左偏,因此我们把操作全部向右进行,这样就可以极大地降低操作复杂度。
性质3:
$dist[x]=dist[rson]+1$,也就是说,任意节点的距离等于其右子树的距离$+1$。
很好理解,由性质二以及外节点的距离为$0$可以得出。
引理1:
如果一棵左偏树的距离为$k$,则这颗左偏树节点数最少为$2^{k+1}-1$。
证明:
因为左偏树的左子树距离一定大于等于右子树的距离,并且左偏树的距离等于右子树距离加一,那么一颗左偏树的距离一定且要求节点数最少时,节点数最少时任意节点的左子树大小等于右子树大小,满足这样性质的二叉树就是完全二叉树。
定理1:
对于一个有$n$个节点的左偏树,最大距离不超过$log(n+1)-1$,即$max{dist}leq log(n+1)-1$。
证明:
设$max{dist}=k$,那么显然节点数最少的左偏树是一棵完全二叉树,此时节点数为$2^{k+1}-1$,故$ngeq 2^{k+1}-1$,移项得:$kleq log(n+1)-1$。
基本操作
1,合并$Merge$
合并操作是可并堆最重要的操作,以小根堆为例,合并$x$与$y$。
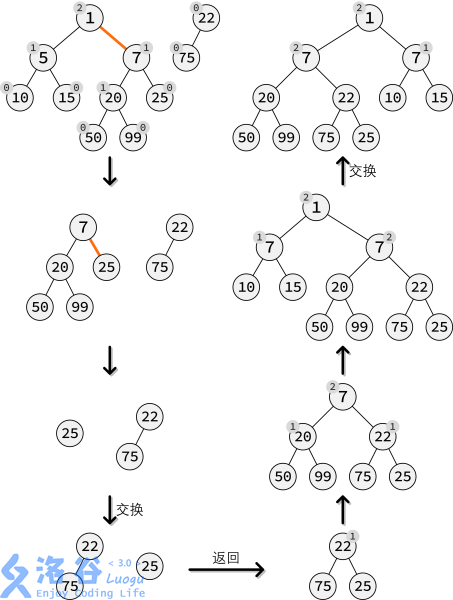
令$x$为$x,y$中权值较小的一个,然后继续向下合并,在$x$的右子树最右链中找到第一个比$y$大的位置,将$y$作为其父亲,然后继续不断递归调用合并$y$的右子树和以该节点为根的右子树即可,同时注意维护相关信息。更新以后可能会发现,右子树$dist$比左子树大,只要交换两个子树即可。
下图为合并过程:
int Merge(int x,int y) { if(!x||!y)return x+y; if(t[x].val>t[y].val||(t[x].val==t[y].val&&x>y)) swap(x,y); int &ul=t[x].ls,&ur=t[x].rs; ur=Merge(ur,y); t[ul].fa=t[ur].fa=x; if(t[ul].dist<t[ur].dist)swap(ul,ur); t[x].dist=t[ur].dist+1; return x; }
2,删除根节点$Erase$
将根节点的权值赋为$-1$,然后合并左右子树,维护相关信息即可。
inline void Erase(int x) { int ul=t[x].ls,ur=t[x].rs; t[x].val=-1;t[ul].fa=0;t[ur].fa=0; t[x].fa=merge(ul,ur); }
3,删除任意节点$Delete$
这里先解释一下,一般来说可并堆是不支持删除某一给定权值的点的,因此我们这里说的任意节点是指知道编号的任意节点。
首先和根节点一样,先把删除节点的权值赋为$-1$,然后合并其左右子树得到新的左偏树,我们再把得到的这个左偏树接到删除节点的父节点上,同时维护父节点的子节点信息。
但是,删除掉节点后我们可能会发现不满足左偏性质了,那么我们就需要判断是否需要交换左右子树,并且要一直向上重复判断,直到到了某一结点时左偏性质没有被破坏了或者已经到了根节点。
int Delete(int x) { int fx=t[x].fa; int ka=merge(t[x].ls,t[x].rs); t[ka].fa=fx; int &ul=t[fx].ls, &ur=t[fx].rs; ul==x ? ul=ka : ur=ka; while( fx ) { if( t[ul].dist < t[ur].dist ) swap( ul,ur ); if( t[fx].dist==t[ur].dist+1 ) return root; t[fx].dist=t[ur].dist+1; ka=fx; fx=t[x].fa; ul=t[fx].ls,ur=t[fx].rs; } return ka; }
4,建树$Build$
如果我们直接一个一个的$Merge$来建树也没有什么问题,但是这样显然效率非常低下(算上$Merge$,这样建树复杂度是$O(nlog n)$的)。
我们可以稍微优化一下,把每个节点当作节点数为$1$的左偏树存入队列中,然后每次取出队首的两个左偏树合并,把合并后的左偏树放入队列,重复操作直到队列中只剩下一个左偏树。
如图:(图中未注明权值)
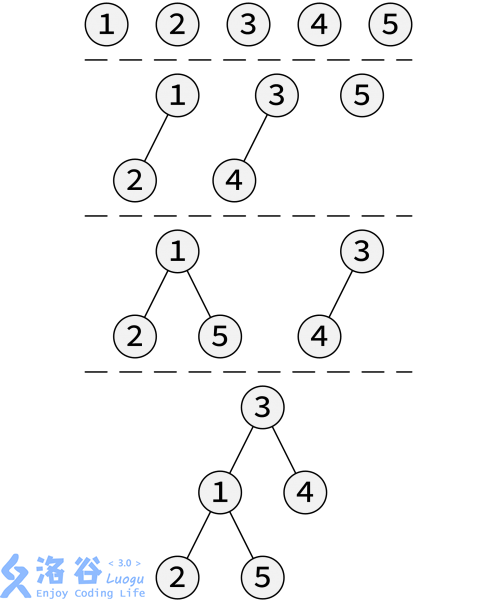
也就是采用两两合并的方法,这样就只需要合并$log n$次,再算上$Merge$的复杂度,这样建树的复杂度基本上可以看作$O(n)$(请读者自证,~~还是作者太懒了~~)。
int Build() { queue<int>Q; for(int i=1; i<=n; ++i) Q.push(i); int x,y,z; while( Q.size()>1 ) { x=Q.front(); Q.pop(); y=Q.front(); Q.pop(); z=Merge(x,y);Q.push(z); } return Q.front(); }
左偏树的应用
常见的左偏树题型
一般来说左偏树能处理所有的二叉堆的问题和所有的可并堆的问题。
但是通常遇到的较难的左偏树题都不是直接进行对集合的操作,这些集合的关系可能更加复杂。最常见的例子就是树上点的集合关系维护的问题。
派遣
一句话题意:从树中选出一个节点作为管理者,然后在它的子树中(包括它自己)选出若干节点,要求使花费总和小于$m$,并且使得收益最大。
【思路】我们可以用左偏树维护点的关系。
除了左右子节点和高度以外,这个左偏树一共还需要维护该节点花费,总花费,总人数三条信息。
从根节点开始$dfs$,然后从下往上递归转移。当转移到第$x$个节点时,我们将它与它所有子节点形成的左偏树合并,然后进行判断,将花费大的节点全部弹出直到花费小于等于$m$为止,然后更新答案即可。当然,这里左偏树要建立大根堆,因为小根堆维护花费和不大于$m$会非常麻烦。然后注意一些细节就行了。
棘手的操作
一句话题意,给你一棵树然后进行一堆蛇皮怪物一般的操作。
【思路】一堆操作真是令人头大,实际上仔细思考的话这些操作还是不难实现的。
需要维护两个左偏树,第一个维护正常的操作信息,第二个维护所有点中的最大值。
【总结】
如果对左偏树不太熟悉,那么第一道例题中是较难看出左偏树的解法的。一般出题人如果考察左偏树的知识点的话,往往不会直接给你裸的集合关系让你维护。(出题人:我怎么能这么容易让你把题给切了呢?)
一般这些集合或者集合内的元素一开始就有很多条件限制(上题中是树状结构),因此往往需要我们自己推导这些集合的关系,然后得出左偏树维护的方法。
而第二题这种纯码农题就不用多说了,全靠一双眼睛$Debug$。
左偏树的可持久化
左偏树的另外一个重要的应用就是可持久化。
为什么左偏树可以可持久化呢?
因为左偏树具有二叉树结构且能动态合并,因此能够可持久化。但是因为左偏树也是带有均摊复杂度的,因此是不能完全可持久化的。
(关于这一点博主听到过不同意见,欢迎大家在评论区讨论)
可持久化左偏树实现起来也非常简单,构建方法类似于可持久化线段树,动态开点就行了。
模板代码:
struct Node { int ls,rs,fa,dist,val; }t[N*20]//可持久化数据结构套路,空间开大点 int siz;//动态开点用 int Merge(int x,int y,int opt)//opt控制是否新建节点 { if(!x||!y)return x+y; if(t[x].val>t[y].val||(t[x].val==t[y].val&&x>y)) swap(x,y); if( opt ) t[++siz]=t[x], x=siz; int &ul=t[x].ls,&ur=t[x].rs; ur=Merge(ur,y); t[ur].fa=x; if(t[ul].dist<t[ur].dist)swap(ul,ur); t[x].dist=t[ur].dist+1; return x; }
其余操作基本不变,按题目要求变化。
为什么你会在比赛中选择左偏树
(填上上面的坑)
有这么多的可并堆可以选择,为什么偏偏就是左偏树最常见呢?
先看一张表:
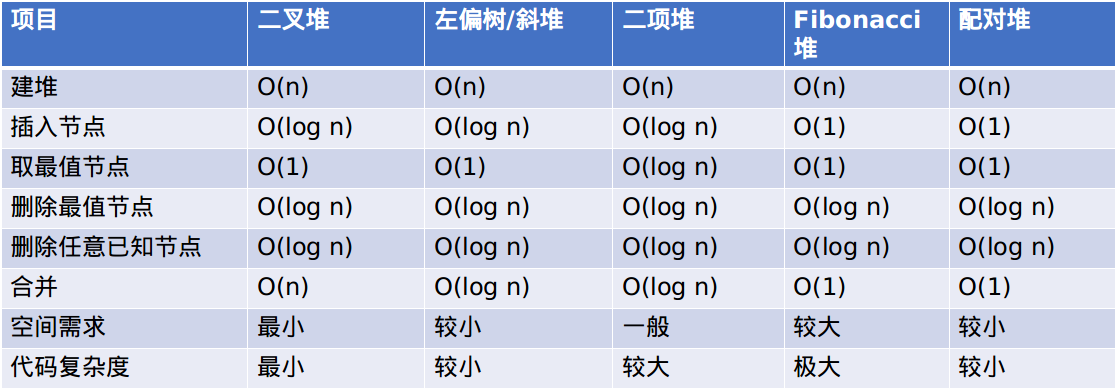
这里还要解释一下,斜堆是一种与左偏树非常类似的可并堆。为了降低操作复杂度,左偏树采用的方法是将重量集中在左子树,而斜堆则是采取一种随机的思想,每次合并完都要交换左右子树,这使得左右子树的大小是随机分配的,因此一般来说,斜堆的均摊复杂度为$O(log n)$,而左偏树则是最坏复杂度$O(log n)$。所以实现的时候,左偏树往往会比斜堆稍快。(当然具体也要看数据咯)
然后二项堆、斐波那契堆虽然复杂度极其优秀,但是编程复杂度极大(尤其是斐波那契堆),考场上选择它们实在是不理智。 (当然如果你是平板电视julao,这话当我没说)
另外关于配对堆,实际上配对堆确实非常优秀,不仅有和斐波那契堆相当的时间复杂度,而且代码实现比较容易,空间需求也大大减小(在不带$decrease\_key$操作的时候甚至比左偏树小)。不过现在配对堆可能并没有那么普及,而且由于均摊复杂度,使得配对堆无法实现可持久化,而且配对堆的复杂度承受在$pop$操作上,所以在$pop$操作频繁的题目中不建议使用。(具体的数据可以参见Wikipedia,这里博主就不放了)
因此左偏树往往是考场上需要使用可并堆时的第一选择。
参考资料:
李煜东:《算法竞赛进阶指南》
黄源河:《左偏树的特点及应用》
以及相关网络资料