将一个5*5的矩阵中最大的元素放在中心,4个角分别放4个最小的元素(顺序为从左到右,从上到下依次从小到大存放),写一函数实现之。用main函数调用

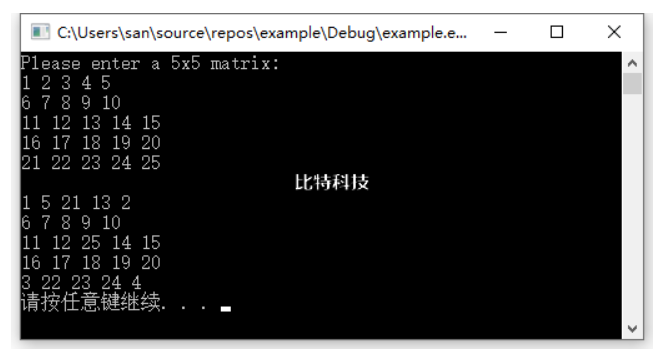
将一个5x5的矩阵中最大的元素放在中心,4个角分别放4个最小的元素(顺序为从左到右,从上到下依次从小到大存放),写一函数实现之。用main函数调用。

解题思路： 将二维数组当做一维数组进行处理比较方便，而二维数组本身就是扁平化存储，所以直接使用首地址即可。

先遍历找到最大值，将其与中间数字交换，而中间数字的下标就是数字总数除以2；

其次寻找四次最小值，每次寻找的时候将最小值的下标记录起来，前提是这个数字如果已经是选中的最小数字之一，则需要跳过，也就是只跟剩余的数字作比较。（第二次开始遍历找最小数字的时候，千万不能与第一个最小数进行比较，否则永远都只有一个最小数）。

答案：

#include <stdio.h>
#include <string.h>
void transform(int *arry, int col_row)
{
    //找到最大值
	int max = arry[0], max_idx;
	for (int i = 0; i < col_row * col_row; i++) {
		if (max < arry[i]) max = arry[i];//找出最大数
		max_idx = i;
	}
	//行列相乘得到总数量，除以2后加1则为中心点（暂时不考虑偶数的情况）
	int center_idx = (col_row * col_row) / 2;
	int tmp = arry[cen ter_idx]; arry[center_idx] = arry[max_idx]; arry[max_idx] = tmp;

	//找到四个最小值
	int min_idx[4];
	for (int i = 0; i < 4; i++) {//循环4次获取到最小值
		int min_tmp = arry[col_row * col_row - 1];
		for (int j = 0; j < col_row * col_row; j++) {//遍历所有数据，逐个比较获取最小值
			int k = 0;
			for (; k < i; k++) {//但是要注意如果某个下标的数据已经是获取过的最小值,则不能进行判断（因为这个肯定是最小的）
				if (j == min_idx[k]) break;
			}
			if (k != i) { continue; }//k和i不同表示j这个坐标已经是找到的最小的几个数字之一，则找下一个判断
			if (min_tmp > arry[j]) { // 相当于在剩下的数中找到最小的那个数字
				min_tmp = arry[j];
				min_idx[i] = j; //并且记录这个数字的位置
			}
		}
	}
    int change_idx[4];//先计算四个角的下标，便于后边进行交换
	change_idx[0] = 0;//第一个要置换的数据的下标，也就是左上角
	change_idx[1] = col_row - 1;//第二个要置换的数据的下标，也就是右上角
	change_idx[2] = col_row * (col_row - 1);//第一个要置换的数据的下标，也就是左下角
	change_idx[3] = (col_row * col_row) - 1;//第一个要置换的数据的下标，也就是右下角
	for (int i = 0; i < 4; i++) {
		int tmp = arry[change_idx[i]]; arry[change_idx[i]] = arry[min_idx[i]]; arry[min_idx[i]] = tmp;
	}
	return ;
}
int main()
{
	int arry[5][5];
	printf("Please enter a 5x5 matrix: 
");
	for (int i = 0; i < 5; i++) {
		for (int j = 0; j < 5; j++) {
			scanf_s("%d", &arry[i][j]);
		} 
	}
	transform(*arry, 5);//将二维数组当做一维数组传入处理，并且传入行列数
	printf("
");
	for (int i = 0; i < 5; i++) {
		for (int j = 0; j < 5; j++) {
			printf("%d ", arry[i][j]);
		}
		printf("
");
	}
	system("pause");
	return 0;
}