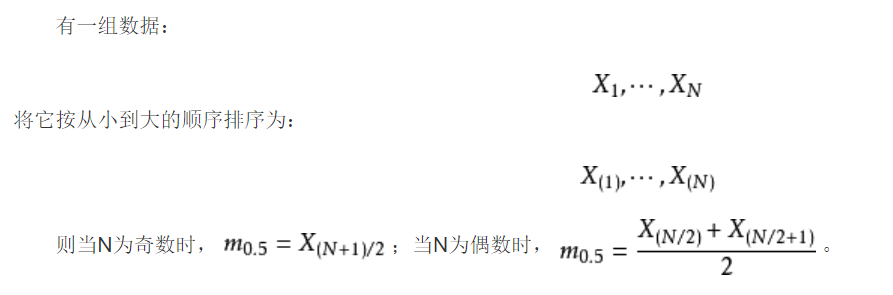定理:
欧拉函数:小于n的正整数中与n互质的数的数目(φ(1)=1)
- 若n为质数则
 ,但n为合数时,并不是小于n的质数的个数,两个合数也可以互质的;
,但n为合数时,并不是小于n的质数的个数,两个合数也可以互质的; - 设m和n是互质的正整数,φ(mn) = φ(m) φ(n);
- 设p是一个质数,φ(p^n) = p^n-p^(n-1);(通过上一条可以证明出来)
欧拉定理:对于任何两个互质的正整数a,m(m≥2)有a^φ(m)≡1(mod m);
费马小定理:当P是质数时,满足 a^(p-1)≡1(mod p);(费马,欧拉:我们想到一块去了。)
算术基本定理:任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积 ,这里
,这里 均为质数,其中指数ai是正整数。这样的分解称为N的标准分解式。
均为质数,其中指数ai是正整数。这样的分解称为N的标准分解式。
四平方和定理:每个正整数均可表示为4个整数的平方和。
哥德巴赫猜想:

1742年6月7日,哥德巴赫写信给欧拉,提出了著名的哥德巴赫猜想:随便取某一个奇数,比如77,可以把它写成三个素数之和,即77=53+17+7;再任取一个奇数,比如461,可以表示成461=449+7+5,也是三个素数之和,461还可以写成257+199+5,仍然是三个素数之和。例子多了,即发现“任何大于5的奇数都是三个素数之和。” 1742年6月30日欧拉给哥德巴赫回信。这个命题看来是正确的,但是他也给不出严格的证明。同时欧拉又提出了另一个命题:任何一个大于2的偶数都是两个素数之和。但是这个命题他也没能给予证明。
哈密顿通路:经过每个顶点刚好一次的路。
哈密顿回路:经过每个顶点刚好一次的回路。
欧拉通路:经过每条边刚好一次的路。(一笔画问题)。奇点数目不超过2个,奇点不会单个出现,就是0个或者2个。

#include <iostream> #include <queue> using namespace std; int cnt[5000]; int main() { int n, m; while (cin >> n >> m) { memset(cnt, 0, sizeof(cnt)); int res = 0; for (int i = 1; i <= m; i++) { int c1, c2; cin >> c1 >> c2; cnt[c1]++; cnt[c2]++; } for (int i = 1; i <= n; i++) { if (cnt[i] & 1) { res++; } } if (res > 2)cout << "No" << endl; else cout << "Yes" << endl; } return 0; }
欧拉回路:经过每条边刚好一次的回路,最后回到起点。所有点的度数均为偶数。
有向图欧拉通路充要条件:D为有向图,D的基图连通,并且所有顶点的出度与入度都相等;或者除两个顶点外,其余顶点的出度与入度都相等,而这两个顶点中一个顶点的出度与入度之差为1,另一个顶点的出度与入度之差为-1。
有向图欧拉回路充要条件:当D的所有顶点的出、入度都相等时,D中存在有向欧拉回路。
杂记
- 最小的素数:2
- 0除余任何数都是 0
- 0!=1
- 补码,一个数 带符号取反+1,就是相反数。比如:-2:ffff,fffe H;+2:0000,0002 H
- a|b,“a整除b”或“b能被a整除 b%a==0;
- 除去11,没有偶数位的回文质数,因为所有偶数位的回文质数一定可以被11整除。
- 两位即以上的素数一定是6的倍数±1
乱记
中位数: