随笔练——单链表相关问题

1.判断一个单链表是否有环

---

•  借助STL里的 set ，java里用hashset是一样的，不需要排序，碰到重复key说明有环。

LNode *isloop(LinkList l) {
    LNode *p = l->next;
    set<LNode*>s;
    while (p) {
        if (s.find(p) != s.end()) {
            return p;
        }
        s.insert(p);
        p = p->next;
    }
    return NULL;
}

• 不借助set也可以通过另一种方式：

一个正常指针一次走一个，一个快指针一次走两个。

如果链表有环，快指针一定会和慢指针相遇，相遇的时候，把快指针扔回头结点，然后两个指针都每次走一个，一定会在 环入口相遇。

LNode* isloop(LinkList l) {
    LNode *pp = l->next, *p = l->next;
    while (pp&&pp->next) {
        pp = pp->next->next;
        p = p->next;
        if (p == pp) {
            pp = l->next;
            while (p != pp) {
                pp = pp->next;
                p = p->next;
            }
            return p;
        }
    }
    return NULL;
}

完整测试代码：

#include <iostream>
#include <set>
using namespace std;
typedef struct LNode {
    struct LNode *next;
    int data;
}*LinkList;

void push_back(LinkList l, int x) {
    LNode *p = l;
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = x;
    while (p->next) {
        p = p->next;
    }
    s->next = p->next;
    p->next = s;
}

LinkList init() {
    LinkList l = (LinkList)malloc(sizeof(LNode));
    l->next = NULL;
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int t;
        cin >> t;
        push_back(l, t);
    }
    return l;
}

void loop(LinkList l) {
    LNode *p = l->next;
    while (p->next)p = p->next;
    p->next = l->next->next->next;
}

LNode *isloop(LinkList l) {
    LNode *p = l->next;
    set<LNode*>s;
    while (p) {
        if (s.find(p) != s.end()) {
            return p;
        }
        s.insert(p);
        p = p->next;
    }
    return NULL;
}

LNode* isloop1(LinkList l) {
    LNode *pp = l->next, *p = l->next;
    while (pp&&pp->next) {
        pp = pp->next->next;
        p = p->next;
        if (p == pp) {
            pp = l->next;
            while (p != pp) {
                pp = pp->next;
                p = p->next;
            }
            return p;
        }
    }
    return NULL;
}
int main() {
    LinkList l = init();
    loop(l);
    cout << isloop1(l)->data << endl;
    return  0;
}

2.判断两个链表是否相交（无环）

---

• 借助set，和第一题思想差不多。

• 不借助set：

首先要搞清楚，如果两个链表相交的话，那他们的最后一个节点一定是同一个。（因为是单链表就一个next，不存在说相交了在分开）。

那么我们就要，先分别遍历两个链表，并得到两个链表的最后一个节点，判断如果是同一个，继续进行，让较长的链表先走掉多出来的长度（遍历时候获取长度），让两个链表在同一起跑线，然后一定会同时在 相交节点处 相遇。

LNode *isintersect(LinkList l1,LinkList l2) {
    LNode *p = l1->next, *q = l2->next;
    int lg1 = 1, lg2 = 1;
    while (p->next) {
        lg1++; 
        p = p->next;
    }
    while (q->next) {
        lg2++;
        q = q->next;
    }
    if (p != q) return NULL;
    int div = abs(lg1 - lg2);
    p = lg1 > lg2 ? l1->next : l2->next;
    q = lg1 > lg2 ? l2->next : l1->next;
    while (div--) {
        p = p->next;
    }
    while (q != p) {
        p = p->next;
        q = q->next;
    }
    return p;
}

 3.判断两个有环链表是否相交

---

 要清楚，单链表相交了之后就分不开了，进了环就出不来了。

所以只有三种情况：1 不相交，2 相交一段时间后，共用一个环， 3 无相交点，直接入环

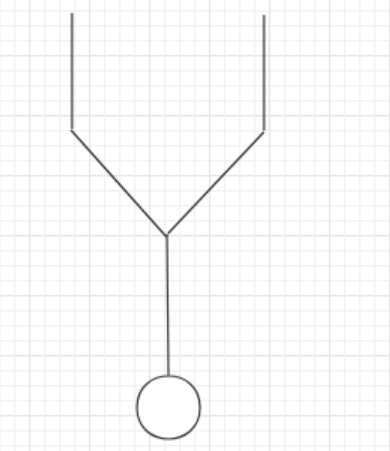
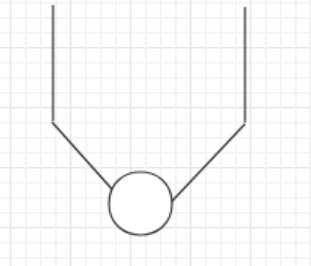
没有进行测试，但思想正确，应该是不会写错的。

LNode* intersect(LinkList l1, LinkList l2) {
    LNode *p1 = isloop(l1);
    LNode *p2 = isloop(l2);
    if (p1 == p2 && p1 != NULL) {
        //说明是第二种
        LNode *t = p1->next;
        p1->next = NULL;
        LNode *q = isintersect(l1, l2);
        p1->next = t;
        return q;
    }
    LNode *t = p1;
    while (p1 != p2) {
        p1 = p1->next;
        if (p1 == t) {
            //第三种
            return p;
        }
    }
    //都没找到，无相交
    return NULL;
}

4. 对单链表进行 快排的partition 过程

---

给定一个基准值，将单链表分成小于，等于，大于三个部分。

第一种思路：

借助数组，把所有value在数组里完成partition之后，再搞回去，这个就不写了。

第二种思路：

进行一次遍历将链表分成三部分，small，euqal，big，最后把它们三个串起来，感觉好像不难，写起来还是挺麻烦的，主要就是，最后，谁空谁不空的，没想到有什么特别好的解决办法，只能一点点判断。

void partition(LinkList l, int x) {
    LNode *sh, *st, *eh, *et, *bh, *bt;
    sh = st = bh = bt = eh = et = NULL;
    LNode *p = l->next;
    while (p) {
        LNode *t = p->next;
        if (p->data < x) {
            if (!sh) sh = st = p;
            else {
                st->next = p;
                st = p;
                //st->next = eh;
            }
        }
        else if (p->data == x) {
            if (!eh) eh = et = p;
            else {
                et->next = p;
                et = p;
            }
        }
        else {
            if (!bh) {
                bh = bt = p;
                bt->next = NULL;
            }
            else {
                p->next = bt->next;
                bt->next = p;
                bt = p;
            }
        }
        p = t;
    }

    //小中大||小中
    if (sh&&eh) {
        st->next = eh;
        et->next = bh;
        l->next = sh;
        return;
    }
    //小||小大
    if (sh) {
        st->next = bh;
        l->next = sh;
        return;
    }
    //中||中大
    if (eh) {
        et->next = bh;
        l->next = eh;
        return;
    }
    l->next = bh;
}

完成测试代码：

#include <iostream>
#include <time.h>
#include <set>
using namespace std;
typedef struct LNode {
    struct LNode *next;
    int data;
}*LinkList;

void push_back(LinkList l, int x) {
    LNode *p = l;
    LNode *s = (LNode *)malloc(sizeof(LNode));
    s->data = x;
    while (p->next) {
        p = p->next;
    }
    s->next = p->next;
    p->next = s;
}

LinkList init() {
    srand(time(0));
    LinkList l = (LinkList)malloc(sizeof(LNode));
    l->next = NULL;
    int n=rand()%20+1;
    for (int i = 0; i < n; i++) {
        int t = rand() % 10 + 1;
        //cin >> t;
        push_back(l, t);
    }
    return l;
}

void partition(LinkList l, int x) {
    LNode *sh, *st, *eh, *et, *bh, *bt;
    sh = st = bh = bt = eh = et = NULL;
    LNode *p = l->next;
    while (p) {
        LNode *t = p->next;
        if (p->data < x) {
            if (!sh) sh = st = p;
            else {
                st->next = p;
                st = p;
                //st->next = eh;
            }
        }
        else if (p->data == x) {
            if (!eh) eh = et = p;
            else {
                et->next = p;
                et = p;
            }
        }
        else {
            if (!bh) {
                bh = bt = p;
                bt->next = NULL;
            }
            else {
                p->next = bt->next;
                bt->next = p;
                bt = p;
            }
        }
        p = t;
    }

    //小中大||小中
    if (sh&&eh) {
        st->next = eh;
        et->next = bh;
        l->next = sh;
        return;
    }
    //小||小大
    if (sh) {
        st->next = bh;
        l->next = sh;
        return;
    }
    //中||中大
    if (eh) {
        et->next = bh;
        l->next = eh;
        return;
    }
    l->next = bh;
}

void print(LinkList l) {
    LNode *p = l->next;
    int sign1 = 1, sign2 = 1;
    while (p) {
        if(sign1&&p->data == 7) {
            cout << endl;
            sign1 = false;
        }
        if (sign2&&p->data > 7) {
            cout << endl;
            sign2 = false;
        }
        cout << p->data << ' ';
        p = p->next;
    }
}

int main() {
    LinkList l = init();
    partition(l,7);
    print(l);
    return  0;
}

5.完成对特殊单链表的拷贝

---

每个节点不光含有Next指针，还都有一个random指针，指向任意节点。

第一种方法：

借助map，每个键值对，key中存储原来的节点，value中存储新节点，新节点的rand指针就指向key对应的value。

LinkList copyList(LinkList l) {
    map<LNode*,LNode*>m;
    LNode *p = l->next;
    LNode *head = (LinkList)malloc(sizeof(LNode));
    while (p) {
        LNode *s = (LinkList)malloc(sizeof(LNode));
        s->data = p->data;
        m.insert(make_pair(p,s));
        p = p->next;
    }
    p = l->next;
    while (p) {
        m[p]->next = m[p->next];
        m[p]->rand = m[p->rand];
        p = p->next;
    }
    head->next = m[l->next];
    return head;
}

第二种方法：

不借助map，每一个copy的节点，先接在原来节点的后面，然后再串起来，并把原来的连起来，说起来容易，写起来，边界上需要特殊注意下。

LinkList copyList(LinkList l) {
    
    LNode *p = l->next;
    LNode *head = (LinkList)malloc(sizeof(LNode));
    while (p) {
        LNode *t = p->next;
        LNode *s = (LinkList)malloc(sizeof(LNode));
        s->data = p->data;
        s->next = p->next;
        p->next = s;
        p = t;
    }
    p = l->next;
    head->next = p->next;
    LNode *pp = p->next;
    while (pp) {
        LNode *t = p->next->next;
        pp->next = pp->next ? pp->next->next : NULL;
        pp->rand = p->rand ? p->rand->next : NULL;
        p->next = p->next->next;
        p = t;
        pp = t ? t->next : t;
    }
    return head;
}