随手练——洛谷-P1002 过河卒（动态规划入门）

题目链接：https://www.luogu.org/problemnew/show/P1002

题目还算良心，提醒了结果可能很大，确实爆了int范围，

这是一开始写的版本，用递归做的，先给地图做标记，每到一个点，这个点可以走的话，选择向下走还是向右走，但是会超时。

#include <iostream>
using namespace std;

int sign[23][23];
int M, N;
int res = 0;
void move(int i, int j) {
    if (i == N && j == M) {
        res++;
        return;
    }
    if (i < N&&sign[i + 1][j] != 1)
        move(i + 1, j);
    if (j < M&&sign[i][j + 1] != 1)
        move(i, j + 1);
}
void make_mark(int x, int y) {
    sign[x - 1][y - 2] = 1;
    sign[x - 1][y + 2] = 1;
    sign[x + 1][y + 2] = 1;
    sign[x + 1][y - 2] = 1;

    sign[x + 2][y - 1] = 1;
    sign[x + 2][y + 1] = 1;
    sign[x - 2][y - 1] = 1;
    sign[x - 2][y + 1] = 1;

    sign[x][y] = 1;
}

int main() {
    int x, y;
    cin >> N >> M >> x >> y;
    make_mark(x, y);
    move(0, 0);
    cout << res << endl;
    return 0;
}

然后改成了动态规划，手画个表就明白了，这是不考虑“马”的因素，到每个点的步数：

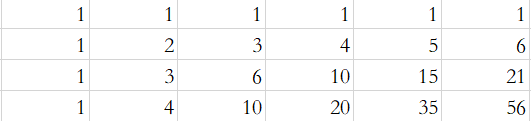
然后代码：

#include <iostream>
using namespace std;

int maze[25][25];
long long dp[25][25];
int dis[][2] = { {-1,-2},{-1,2},{1,2},{1,-2},{2,-1},{2,1},{-2,-1},{-2,1} };
int M, N, x, y;

int main() {
    cin >> N >> M >> x >> y;
    N++; M++; x++; y++;//起点用(1,1)做，后面不会出现下标越界情况，所有点都+1
    maze[x][y] = 1;
    for (int i = 0; i < 8; i++) {
        //标记马的位置，全局数组多开了几个，可以不做越界判断
        maze[x + dis[i][0]][y + dis[i][1]] = 1;
    }
    dp[0][1] = 1;//使得在循环内能够正常初始化 起点 (1,1)
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            if (maze[i][j])continue;
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    cout << dp[N][M] << endl;
    return 0;
}