省选测试6
T1
给出一个(n)个点(m)条边的无向图, 求(i(2<=i<=n))在不经过到1号点的最短路径上的第一条边的情况下, 到1号点的路径长度最小值.
数据保证(i)号点到1号点的最短路径上的第一条边是唯一确定的.
(n <= 1e5, m <= 2e5).
正解是左偏树或者线段树合并, (O(nlog n))的.
机房大佬想了个不那么麻烦的方法, 启发式合并 + 优先队列, (O(nlog^2 n))的, 也能过.
首先我们可以求出所有点到1号点的最短路, 然后就可以建出一颗最短路树(以1为根节点)来, 也就是(dis[y]=dis[x] + val[x, y])的那些边就是最短路树中的边.
对于这个题目, 假设我们当前要求点(x)的答案, 那么我们是不可以选((fa[x],x))这条边的, 我们只能从(x)选出一个点(u), 包括(x), 找到一条非树边(不在最短路树上的边)((u,v)), 然后在计算(x)的答案, 注意这个(v)一定不是在(x)的子树内的. (x)的答案就是(dis[u] - dis[x]+val[u, v]+dis[v]).
我们可以对每个点(x)搞一个优先队列, 然后把以(x)为根的子树内的非树边都加入优先队列中, 每次取出一个(-dis[x]+val[u, v]+dis[v])最小的就好了, 注意判断(v)要在这颗子树外.
然后启发式合并父亲和儿子的优先队列就好了.
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 1e5 + 5, inf = 2e9;
int n, m, cnt, tot;
int d[N], ans[N], siz[N], dfn[N], vis[N], pre[N], las[N], head[N];
vector <int> v[N];
struct edge { int f, to, nxt, val; } e[N << 2];
struct Edge { int f, x, y, val; } E[N << 1];
void add(int x, int y, int z) {
e[++ cnt].nxt = head[x]; head[x] = cnt; e[cnt].to = y; e[cnt].val = z;
}
void run_dij() {
priority_queue <pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
for(register int i = 1;i <= n; i++) d[i] = inf;
d[1] = 0; q.push(make_pair(0, 1));
while(q.size()) {
int x = q.top().second; q.pop();
if(vis[x]) continue ; vis[x] = 1;
for(register int i = head[x]; i ; i = e[i].nxt) {
int y = e[i].to;
if(d[y] > d[x] + e[i].val) {
d[y] = d[x] + e[i].val;
pre[y] = x; las[y] = i;
q.push(make_pair(d[y], y));
}
}
}
for(register int i = 2;i <= n; i++) e[las[i]].f = e[las[i] ^ 1].f = 1;
// for(int i = 1;i <= n; i++) cout << d[i] << " "; cout << "
";
}
void get_tree(int x, int Fa) {
siz[x] = 1; dfn[x] = ++ tot;
for(int i = head[x]; i ; i = e[i].nxt) {
int y = e[i].to; if(y == Fa || !e[i].f) continue ;
// cout << x << " " << y << "!!!
";
get_tree(y, x); siz[x] += siz[y];
}
}
priority_queue <pair<int, int> , vector<pair<int, int> >, greater<pair<int, int> > > q[N];
int rt[N];
void get_ans(int x, int Fa) {
for(register int i = head[x]; i ; i = e[i].nxt) {
int y = e[i].to; if(y == Fa || !e[i].f) continue ;
get_ans(y, x);
}
// cout << x << "----------->
";
for(register int i = 0;i < (int) v[x].size(); i++) {
int j = v[x][i];
int u = E[j].x, v = E[j].y;
if(v == x) swap(u, v);
if(v == Fa) continue ;
// cout << j << ":" << u << " " << v << "
";
if(dfn[v] < dfn[x] || dfn[v] > dfn[x] + siz[x] - 1)
q[rt[x]].push(make_pair(E[j].val + d[v] + d[u], j));
}
for(register int i = head[x]; i ; i = e[i].nxt) {
int y = e[i].to; if(y == Fa || !e[i].f) continue ;
if(q[rt[y]].size() > q[rt[x]].size()) {
while(q[rt[x]].size()) {
pair <int, int> tmp = q[rt[x]].top(); q[rt[x]].pop();
q[rt[y]].push(tmp);
}
swap(rt[x], rt[y]);
}
else {
while(q[rt[y]].size()) {
pair <int, int> tmp = q[rt[y]].top(); q[rt[y]].pop();
q[rt[x]].push(tmp);
}
}
}
int res = 0;
while(q[rt[x]].size()) {
int tmp = q[rt[x]].top().first, to = q[rt[x]].top().second;
int u = E[to].x, v = E[to].y;
if(dfn[u] < dfn[x] || dfn[u] > dfn[x] + siz[x] - 1 || dfn[v] < dfn[x] || dfn[v] > dfn[x] + siz[x] - 1) {
// cout << to << "!!!
";
res = tmp - d[x]; break ;
}
q[rt[x]].pop();
}
if(!res) ans[x] = -1; else ans[x] = res;
}
int main() {
freopen("pal.in","r",stdin); freopen("pal.out","w",stdout);
n = read(); m = read(); cnt = 1;
for(register int i = 1, x, y, z;i <= m; i++) {
x = read(); y = read(); z = read();
add(x, y, z); add(y, x, z);
E[i].x = x; E[i].y = y; E[i].val = z;
v[x].push_back(i); v[y].push_back(i);
}
run_dij();
for(int i = 1;i <= n; i++) rt[i] = i;
get_tree(1, 0); get_ans(1, 0);
for(int i = 2;i <= n; i++) printf("%d
", ans[i]);
fclose(stdin); fclose(stdout);
return 0;
}
/*
4 5
1 2 2
1 3 2
3 4 4
3 2 1
2 4 3
*/
T2
给定一张连通无向图(G=(V,E))和一个质数(P), 其中(V)是点集(E)是边集.
图中的每条边有三种权值(A,B,C), 但同一条边的两个方向上的权值不一定相等, 更具体的, 他们满足以下条件:
1.对于任意无向边((u,v)in E)有:
[A(u,v) equiv -A(v,U) mod P \
B(u,v) equiv B(v,U) mod P \
C(u,v) equiv -C(v,U) mod P \
]
2.对于任意节点(vin V)有:
[displaystyle sum_{(v,w)in E} C(v,w) equiv 0 mod P
]
3.对于图中的每一个环(<v_0,v_1,...,v_{n-1},v_n>),其中(v_0 = v_n)且((v_i,v_{i+1}in E)),有:
[displaystyle sum_{i=0}^{n-1} B(v_i, v_{i+1})*C(v_i,v_{i+1}) equiv sum_{i=0}^{n-1} A(v_i, v_{i+1}) mod P
]
现在给定图中每条边的权值(A,B), 请你求出(C)的取值.数据保证有唯一解.
(n <= 100, m <= 2000, P <= 1e18, 0 <= a,b < P, b>0).
高斯消元.
对于第三个条件, 我们把它转换一下形式:
[displaystyle sum_{i=0}^{n-1} B(v_i, v_{i+1})*C(v_i,v_{i+1}) equiv sum_{i=0}^{n-1} A(v_i, v_{i+1}) mod P \
displaystyle sum_{i=0}^{n-1} B(v_i, v_{i+1})*C(v_i,v_{i+1}) - A(v_i, v_{i+1}) equiv 0 mod P \
displaystyle sum_{i=0}^{n-1} D(v_i, v_{i+1}) equiv 0 mod P
]
然后对于任意一个环上的两个点(x,y), 我们又可以知道:
[displaystyle sum_{x->y} D(v_i, v_{i+1}) + sum_{y->x} D(v_i,v_{i+1}) equiv 0 mod P
]
根据第一个条件, 我们可以知道 : (D(i,j)=-D(j,i)).
所以我们又有:
[displaystyle sum_{(x->y)_1} D(v_i, v_{i+1}) equiv sum_{(x->y)_2} D(v_i,v_{i+1}) mod P
]
什么意思呢? 就是从(x)到(y)的任意两条不同的路径, 他们的(D)值总和相等.
于是我们定义(f(x))代表从1号节点到(x)节点的任意一条路径的(D)值总和.(因为所有到(x)的路径的(D)值都相等嘛)
根据第二个条件, 我们就可以得到(n)个等式 :
[displaystyle sum_{(u,v)in E} C(u, v) equiv 0 mod P \
displaystyle sum_{(u,v)in E} frac{D(u, v) + A(u,v)}{B(u,v)} equiv 0 mod P \
displaystyle sum_{(u,v)in E} frac{f(v) - f(u) + A(u,v)}{B(u,v)} equiv 0 mod P \
]
然后高斯消元求出每个点的(f(x))就好了. (O(n^3))
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 205, M = 2005;
int n, m;
vector <int> v[N];
long long P;
long long f[N][N];
struct edge { int x, y; long long a, b; } e[M << 1];
long long mul(long long x, long long y) {
y = (y % P + P) % P;
long long res = 0;
while(y) { if(y & 1) res = (res + x) % P; x = (x + x) % P; y >>= 1; }
return res;
}
long long ksm(long long x, long long y) {
long long res = 1ll;
while(y) { if(y & 1) res = mul(res, x); x = mul(x, x); y >>= 1; }
return res;
}
void Gauss() {
for(register int i = 1;i <= n; i++) {
int r = i;
for(register int j = i + 1;j <= n; j++) if(f[r][i] < f[j][i]) r = j;
if(r != i)
for(register int j = i;j <= n + 1; j++) swap(f[r][j], f[i][j]);
long long tmp = ksm(f[i][i], P - 2);
for(register int j = i;j <= n + 1; j++) f[i][j] = mul(f[i][j], tmp);
for(register int j = i + 1;j <= n; j++) {
tmp = f[j][i];
for(register int k = i;k <= n + 1; k++) f[j][k] = ((f[j][k] - mul(f[i][k], tmp)) % P + P) % P;
}
}
for(register int i = n - 1;i >= 1; i--)
for(register int j = n;j > i; j--)
f[i][n + 1] = ((f[i][n + 1] - mul(f[i][j], f[j][n + 1]) % P) + P) % P;
}
int main() {
// freopen("graph.in","r",stdin); freopen("graph.out","w",stdout);
n = read(); m = read(); P = read();
for(register int i = 1;i <= m; i++) {
e[i].x = read(); e[i].y = read(); e[i].a = read(); e[i].b = read();
v[e[i].x].push_back(i);
e[i + m].x = e[i].y; e[i + m].y = e[i].x; e[i + m].a = -e[i].a; e[i + m].b = e[i].b;
v[e[i].y].push_back(i + m);
}
for(register int x = 1;x < n; x++) {
for(register int i = 0; i < (int) v[x].size() ; i++) {
int j = v[x][i], y = e[j].y;
long long A = e[j].a, B = ksm(e[j].b, P - 2);
(f[x][x] -= B) %= P; (f[x][y] += B) %= P; (f[x][n + 1] -= mul(A, B)) %= P;
}
}
Gauss();
for(register int i = 1;i <= m; i++) {
register int x = e[i].x, y = e[i].y;
long long D = f[y][n + 1] - f[x][n + 1];
long long C = (mul((D + e[i].a) % P, ksm(e[i].b, P - 2)) + P) % P;
printf("%lld
", C);
}
fclose(stdin); fclose(stdout);
return 0;
}
/*
4 5 19
1 2 1 1
2 3 0 1
1 4 1 2
3 1 1 1
4 2 0 1
*/
T3
有一个(n*m)的网格, 有些格子里面有球, 两个相邻的球之间可以插入木棍.
要求 : 如果可以任意安排(k)个木根的位置, 那么为了插入所有木棍至少要给木匠多少费用.
对于任意的(1<=k<=q)输出答案, (q)为可以插入的木棍总数.
(1<=n,m<=40).
费用流
首先我们考虑(A=B)的情况. 如果一个球连着0个或1个, 那它是没有花费的. 如果连着2个木棍, 那么就有(A)的花费, 如果连着(3)个木棍, 那么就有(3A)的花费, 如果连着4个木棍, 那么就有(6A)的花费.
所以我们可以考虑这样连边. 先把所有点黑白染色. 然后(s)向所有黑点连4条流量为1, 费用为(0, A, 2A, 3A)的边(前提是这个黑点可以连4个木棍).这些黑点再向可以连的那些白点连1条流量为1, 费用为0的边, 然后这些白点向(t)也是连那4条边.
如果(A < B)呢? 我们接着上面的考虑, 如果说1个球连了大于等于2个木棍, 那么它就可能会多(B-A)的花费.
我们考虑把一个点(x)拆成3个点(x,x_1,x_2).(x_1)代表如果当前球(x)纵向的连了两个球, 那么就会多出(B-A)的花费, 于是连两条流量为1, 得用非别为(0, B-A)的边. (x_2)代表当前球横向的连了两个球, 连边方式同(x_1).
(x_1)向对应的纵向的那两个白点连边的(y_1)连边, (x_2)对应向横向的那两个白点的(z_2)连边.
然后跑最小费用最大流就好了.
注意题目要求输出(q)次答案, 我们不需要重新跑(q)次, 每次(dinic)增广就相当于多加了一条边, 跑(q)次增广就好了.
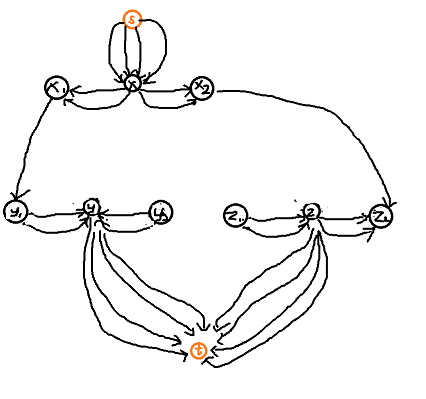
放个连边的图吧 :
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 1000, M = 3e7, inf = 2e9;
int n, m, s, t, T, A, B, q_, cnt, tot;
long long ans;
int d[N * N], du[N * N], pre[N * N], col[N * N], las[N * N], head[N * N], id[N][N];
char s_[N][N];
vector <int> v[N * N];
struct edge { int f, c, to, nxt; } e[M];
void add(int x, int y, int z1, int z2) {
e[++ cnt].nxt = head[x]; head[x] = cnt; e[cnt].to = y; e[cnt].f = z1; e[cnt].c = z2;
e[++ cnt].nxt = head[y]; head[y] = cnt; e[cnt].to = x; e[cnt].f = 0; e[cnt].c = -z2;
}
void get_col(int x, int Col) {
col[x] = Col;
for(int i = 0;i < (int) v[x].size(); i++) {
int y = v[x][i]; if(col[y]) continue ;
get_col(y, 3 - Col);
}
}
void bfs() {
for(int i = 0;i <= t; i++) d[i] = inf;
queue <int> q; d[s] = 0; q.push(s);
while(q.size()) {
int x = q.front(); q.pop();
for(int i = head[x]; i ; i = e[i].nxt) {
int y = e[i].to;
if(e[i].f && d[y] > d[x] + e[i].c) {
d[y] = d[x] + e[i].c;
pre[y] = x; las[y] = i;
q.push(y);
}
}
}
}
int main() {
freopen("trouble.in","r",stdin); freopen("trouble.out","w",stdout);
T = read();
n = read(); m = read(); A = read(); B = read();
for(int i = 1;i <= n; i++) cin >> (s_[i] + 1);
q_ = read();
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
if(s_[i][j] == '0') id[i][j] = ++ tot;
cnt = 1; s = 0; t = tot * 3 + 1;
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++) {
if(s_[i][j] == '1') continue ;
int x = id[i][j];
if(i != 1 && s_[i - 1][j] == '0') v[x].push_back(id[i - 1][j]), du[x] ++;
if(j != 1 && s_[i][j - 1] == '0') v[x].push_back(id[i][j - 1]), du[x] ++;
if(i != n && s_[i + 1][j] == '0') v[x].push_back(id[i + 1][j]), du[x] ++;
if(j != m && s_[i][j + 1] == '0') v[x].push_back(id[i][j + 1]), du[x] ++;
}
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++) {
if(s_[i][j] == '1' || col[id[i][j]]) continue ;
get_col(id[i][j], 1);
}
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++) {
if(s_[i][j] == '1') continue ;
int x = id[i][j];
if(col[x] == 1) {
for(int k = 0;k < du[x]; k++)
add(s, x, 1, A * k);
add(x, x + tot, 1, 0); add(x, x + tot, 1, B - A);
add(x, x + 2 * tot, 1, 0); add(x, x + 2 * tot, 1, B - A);
if(i != 1 && s_[i - 1][j] == '0') add(x + tot, id[i - 1][j] + tot, 1, 0);
if(j != 1 && s_[i][j - 1] == '0') add(x + 2 * tot, id[i][j - 1] + 2 * tot, 1, 0);
if(i != n && s_[i + 1][j] == '0') add(x + tot, id[i + 1][j] + tot, 1, 0);
if(j != m && s_[i][j + 1] == '0') add(x + 2 * tot, id[i][j + 1] + 2 * tot, 1, 0);
}
if(col[x] == 2) {
for(int k = 0;k < du[x]; k++)
add(x, t, 1, A * k);
add(x + tot, x, 1, 0); add(x + tot, x, 1, B - A);
add(x + 2 * tot, x, 1, 0); add(x + 2 * tot, x, 1, B - A);
}
}
for(int i = 1;i <= q_; i++) {
bfs();
ans = ans + d[t];
int now = t;
while(now != s) {
e[las[now]].f -= 1;
e[las[now] ^ 1].f += 1;
now = pre[now];
}
if(T >= 8 && T <= 12) printf("%d
", !ans ? 0 : 1);
else printf("%lld
", ans);
}
fclose(stdin); fclose(stdout);
return 0;
}
/*
0
2 4 20 50
0001
0001
7
*/